题意:找到两条边路径上的必经点个数
分析:一看到这个题,立刻想到之前的压力应该不是问题吧,
这个题应该可以说是压力的简单版,但又与压力有点区别
首先,看到这种必经点的题,立刻圆方树搞起应该已经不是啥问题了吧
重点是接下来怎么做,边于边怎么找路径必经点呢?
这里我介绍两种比较简练(但不保证简单)的思路
第一种,现在的问题其实就是不知道从哪两个圆点开始跑lca以及统计等等的操作
那么我们干脆不跑圆点,改跑方点...
现在可能还有人不明白现在的问题到底是啥,我举个例子
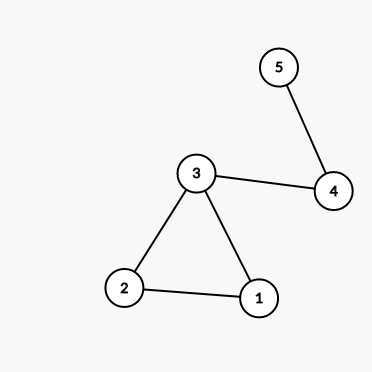
这是原图
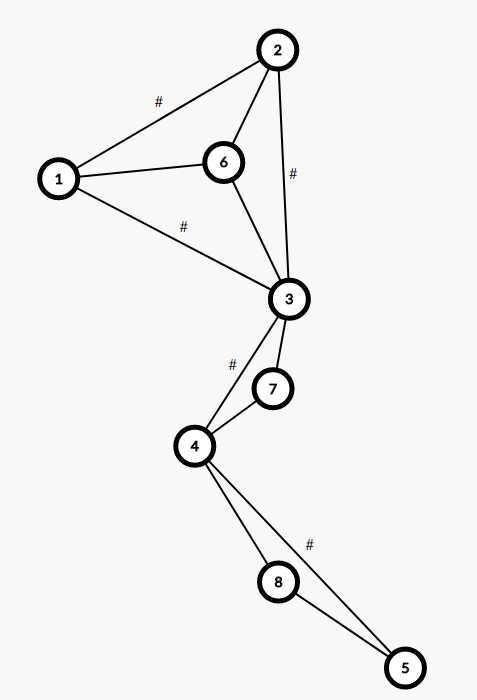
跑完圆方树后6,7,8是方点,#表示这条边不存在
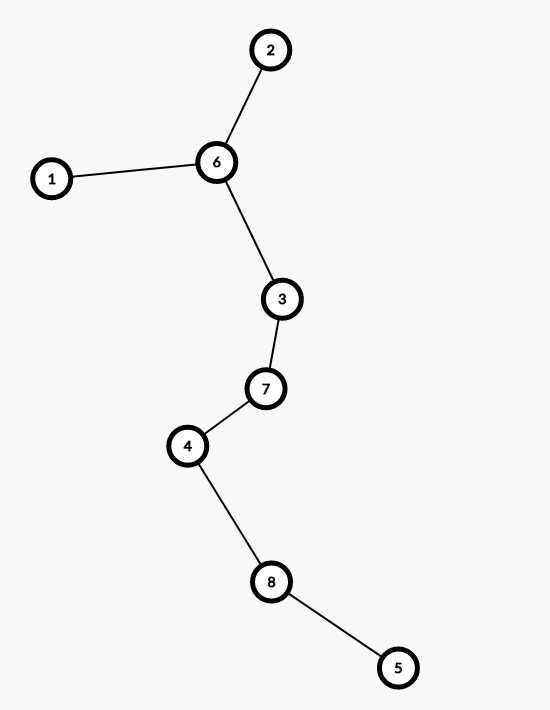
再给个清楚点的圆方树
现在我要找从12这条边到45这条边路径上的必经点,我不知道是找从1到5的还是找1到4的还是找2到4的还是找2到5的
还有一个问题就是,如果我们就算选出了两个点,比如1到5的,那1和5一定是必经点吗,比如我们的压力这道题,显然1和5是必经点,
但如果1和2在同一个环中(先不考虑是什么样的环,先理解这个问题)那么显然1和2都不是必经的点,因为我到达这条边既可以从1也可以从2,
同理,45也是这样
好了,现在知道了问题是什么,再回看那句思路
我们干脆不跑圆点,改跑方点
为什么这能解决问题呢?
还是可以举几个例子
如上面那个圆方树,如果我要求的是23这条边到45这条边上的必经点,显然,23对应的方点是6,45对应的方点是8
那么如果我直接找6到8上的圆点是不是正好能找到正确结果(可以配合原图(圆方树之前的图)食用)
这是边其中一个端点是必经的情况
而这对于刚刚我们的那种两端点都不必经的情况也适用,比如12到45
所以这种方法其实是完美的解决了这个问题
但这又产生了一个新的问题,如何知道哪条边对应哪个点双呢?
我水平有限,有人想出来可以跟我讨论[呲牙],(别吐槽我浪费你们这么长时间看一个不会的做法就行)
第二种,可以说是非常妙的了
先说结论,只需要将这两个边4个点任意两两跑一遍,最后取最大值即可
先别急着疑惑,慢慢来
首先就是这题求两圆点之间圆点个数(不包括x与y)的方法
这个很简单,(deep[x]+deep[y]-2*deep[lca(x,y)])/2-1,deep[x]是x的深度,根节点为0,解释一下
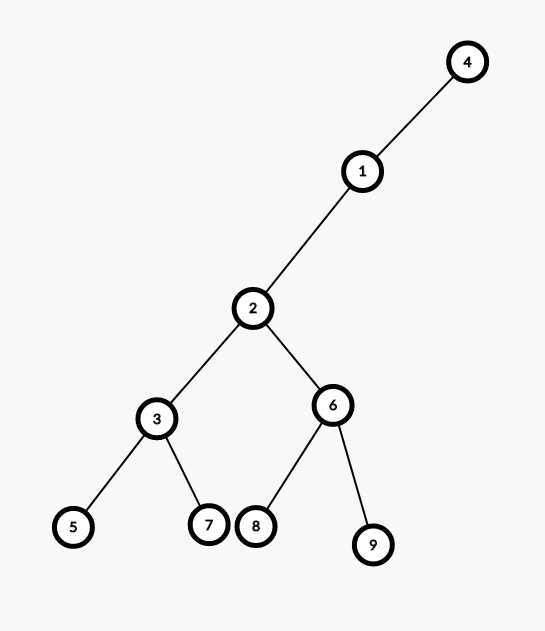
对于这颗树来说,因为圆点与方点交替分布,不妨以4(圆点)为根节点,以1,3,6为方点
那么deep[x]表示的其实就是x的祖先一共有多少个,拿5与8举例子
deep[5]=4表示了他祖先1,2,3,4这四个节点
deep[8]=4表示了他祖先1,2,6,4这四个节点
lca(5,8)=2
deep[2]=2表示了他祖先1,4这两个节点
deep[5]-deep[2]=2表示了2,3这两个节点
deep[8]-deep[2]=2表示了2,6这两个节点
显然这样这两条路上就都是圆点和方点交替了,除以二就能得到圆点的总个数
但注意,这两条路上2这个圆点重复了,所以要-1
好,知道了这个再去想为什么任选两个节点然后取最大值就行了呢?
还是先通过例子来看看

还是先选23与45这两条路
如果是选的3,4这两个点来跑的话,显然会漏掉原本必经的两个点3,4,因为我们这个方法求的是不算x,y的路径上必经点
但如果选的是2和5,就会发现正好会算上3和4,还不会算上2和5,正好与我们想要的结果一致
再看12与45这两条路
无论你选的是1还是2,1,2都不会被选入必经点中,也符合了正确答案
那么这是为什么呢?
其实,这个题的意思也可以理解为两条路中经过的割点数,当然如果单纯是两点之间的必经点也可以理解为路径中的割点数,不过端点也选上罢了,
这很好理解,因为割点的定义就是断掉这个点你就过不去了
而在圆方树中,割点就是非叶子结点的圆点,而非割点则就是叶子结点,如果在圆方树后,该边的两个端点都是叶子结点,也就是说都不是割点,那自然不选
而只要在路径上的端点是割点,那从另一个端点为起点的路径一定会经过这个点,自然就将他算上了
最后,本文没有讲圆方树以及lca或是dfs的具体处理细节,默认你们已经把压力那题敲的滚瓜烂熟了[呲牙]
实在不会那些比较基本的tarjan,lca或是dfs的话,emm
我好像暂时也没啥办法,毕竟在这种思维题上讲基础好像有点浪费时间[滑稽]
代码:
#include<cstdio> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int maxn=2e4+1; const int maxm=4e5+1; const int maxlg=2e1+1; struct Node { int to,next; }e[maxm<<1],e2[maxn<<2]; struct edge { int x,y; }a[maxm]; int head[maxn]; int head2[maxn<<1]; int dfn[maxn]; int low[maxn]; int deep[maxn<<1]; int fa[maxn<<1][maxlg]; bool vis[maxn<<1]; vector<int> q; int cnt,tar_cnt,cnt2,fang,n; void add(int x,int y) { e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt; } void add2(int x,int y) { e2[++cnt2].to=y; e2[cnt2].next=head2[x]; head2[x]=cnt2; } void tarjan(int x) { dfn[x]=low[x]=++tar_cnt; q.push_back(x); for(int i=head[x];i;i=e[i].next) { int v=e[i].to; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]) { int now; do { now=q.back(); add2(now,fang); add2(fang,now); q.pop_back(); }while(now!=v); add2(x,fang);add2(fang++,x); } } else low[x]=min(low[x],dfn[v]); } } void dfs(int x,int f) { for(int i=head2[x];i;i=e2[i].next) { int v=e2[i].to; if(v!=f) { fa[v][0]=x; deep[v]=deep[x]+1; dfs(v,x); } } } int ask(int x,int y) { if(deep[x]<deep[y]) swap(x,y); int now=deep[x]-deep[y]; for(int i=0;now;i++,now>>=1) if(now&1) x=fa[x][i]; if(x==y) return x; for(int i=maxlg-1;i>=0;i--) { if(fa[x][i]!=fa[y][i]) { x=fa[x][i]; y=fa[y][i]; } } return fa[x][0]; } int chuli(int x,int y) { int fax=ask(x,y); return (deep[x]+deep[y]-2*deep[fax])/2-1; } int main() { int m,q,x,y; while(scanf("%d%d",&n,&m)!=EOF&&n) { memset(head,0,sizeof(head)); memset(head2,0,sizeof(head2)); memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(vis,0,sizeof(vis)); memset(fa,0,sizeof(fa)); cnt=cnt2=tar_cnt=0; fang=n+1; for(int i=1;i<=m;i++) { scanf("%d%d",&x,&y); add(x,y);add(y,x); a[i].x=x,a[i].y=y; } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i),dfs(i,-1); for(int i=1;i<maxlg;i++) for(int j=1;j<fang;j++) fa[j][i]=fa[fa[j][i-1]][i-1]; scanf("%d",&q); while(q--) { scanf("%d%d",&x,&y); int ans=0; ans=max(ans,chuli(a[x].x,a[y].x)); ans=max(ans,chuli(a[x].x,a[y].y)); ans=max(ans,chuli(a[x].y,a[y].x)); ans=max(ans,chuli(a[x].y,a[y].y)); printf("%d\n",ans); } } return 0; }
原文:https://www.cnblogs.com/lin4xu/p/12829157.html