实践部分:
实际上如果是熟悉matlab操作的大神们应该改会发现这些包和matlab里面的是相通的
python 大杂烩实锤
了解微分方程模拟
时间关系,看看实现例子,然后自己写
理论部分:
知乎专栏——AI和金融模型——第一篇文章开始
重点:
一开始不知道用函数怎么实现,还以为布朗运动模拟运动的模拟要积分,实际上运用的是正态分布+时间函数求和,
因为时间点是离散的,用定义法求积分,
dx = a*dt + b*dz,∑a*dt = T,dz=e*sqrt(dt),e~(0,1),∑dz=(sqrt(dt))*∑ e
伊藤引理也是这样,只是它的积分式是微分方程,由公式:dS/S=u* dt+e* o* sqrt(dt),求 S ,需要用微分方程来推导
最后会得到几何布朗运动的基本公式
代码实现:

1 # -*- coding: utf-8 -*- 2 """ 3 Created on Mon May 4 20:43:06 2020 4 5 @author: 10913 6 """ 7 import numpy as np 8 import matplotlib.pyplot as plt 9 10 ‘‘‘ 11 12 T=10 13 dt=0.1 14 n=round(T/dt)#dimension 15 t=np.linspace(0,T,n) 16 e=np.random.standard_normal(size=n) 17 z=np.cumsum(e)*np.sqrt(dt) 18 a=0.1 19 b=0.2 20 x=a*t+b*z; 21 plt.plot(t,x) 22 plt.show() 23 24 25 ‘‘‘ 26 27 ‘‘‘ 28 几何布朗运动: 29 St=S0*exp(ut) 30 St=S0*exp(u t+o e sqrt(dt)) 31 ut求和===T 32 o e sqrt(dt)求和为o cumsum(e)*np.sqrt(dt) 33 St=S0*exp(a t+b z) 34 随机变量e服从标准正态分布 35 36 ‘‘‘ 37 D=250 #250个交易日 38 T=1.0 #总时间1年 39 dt=T/D #单位时间 40 s0=100 #初始价格 41 i=10 #算i-1次 42 n=D+1 #为了能够从0开始 而不是[1,250] 43 st=np.zeros((i,n)) 44 45 a=0.15 #平均收益率--连续复利的收益率 46 b=0.3 #收益率标准差 47 #dimension 48 plt.subplot(212) 49 for g in range(1, i): 50 t=np.linspace(0,D,n) 51 e=np.random.standard_normal(size=n) #随机变量e 52 z=np.cumsum(e)*np.sqrt(dt) #随机变量e和时间t共同决定的变量z 53 x=a*T+b*z; #几何布朗运动得到的x波动率 54 st[g]=s0*np.exp(x) #如果用z就是标准布朗运动 55 #st[g][0]=s0 #起点波动率不为0.... 56 plt.plot(t,st[g],label=‘St ‘+str(g)) 57 58 plt.legend() 59 60 plt.show() 61 ‘‘‘ 62 另一种写法 63 64 S=np.zeros((M+1,I)) 65 66 S[0]=S0 #定义S[0]=S0 67 68 for t in range(1,M+1): 69 70 S[t]=S[t-1]*np.exp(mean*dt+sigma*np.sqrt(dt)*np.random.standard_normal(I)) 71 72 ‘‘‘
执行结果:
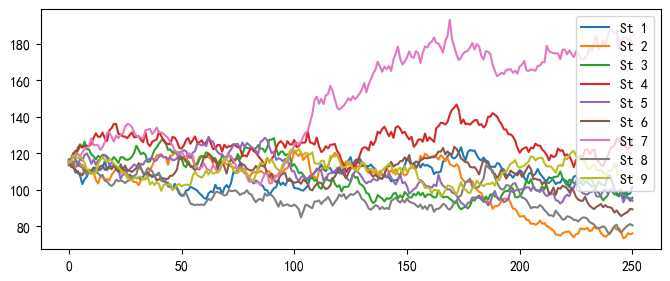
python数据可视化分析速成笔记_2-2_布朗运动/几何布朗运动(伊藤过程)实现的demo
原文:https://www.cnblogs.com/KID-yln/p/12823748.html