前言:
由上一讲我们知道,计算机硬件层面为我们提供了门电路,可以实现“与”、“或”、“非”这样的单比特逻辑运算。后续的电路其实就是这些门电路组合而成的的。
一、异或门和半加器
假如我们要计算8位二进制的加法,使用手算应该怎么算呢?我们会找到一张草稿纸,第一行前两行写上要加起来的两个数然在第三行准备写计算结果: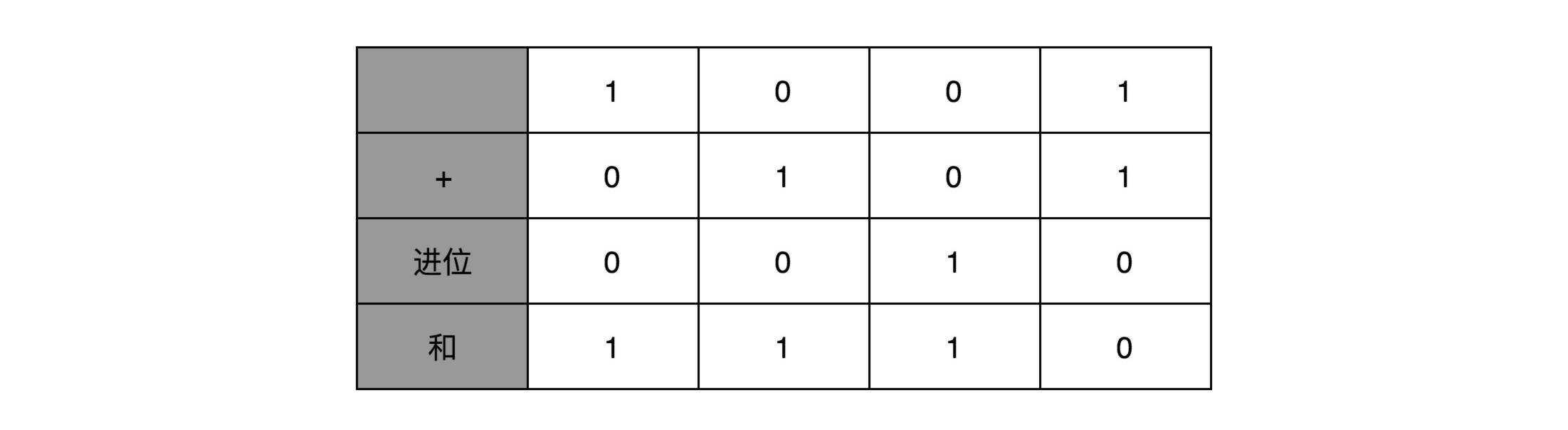
由上图我们可以发现,我们需要从低位开始关注当前位的计算结果和是否进位,而当前位的结果正好取决于参与参与计算的两位是否相同,规律是相同则结果为0,不同则结果为1,看到没有这恰好是异或门的逻辑,因此我们可以使用异或门来实现加法,但这样的电路只关注了当前位,却没处理进位;而是否进位的逻辑是若运算的两位同为1则进位1,否则进位为0,将这样的一个异或门和与门打包就是一个半加器。
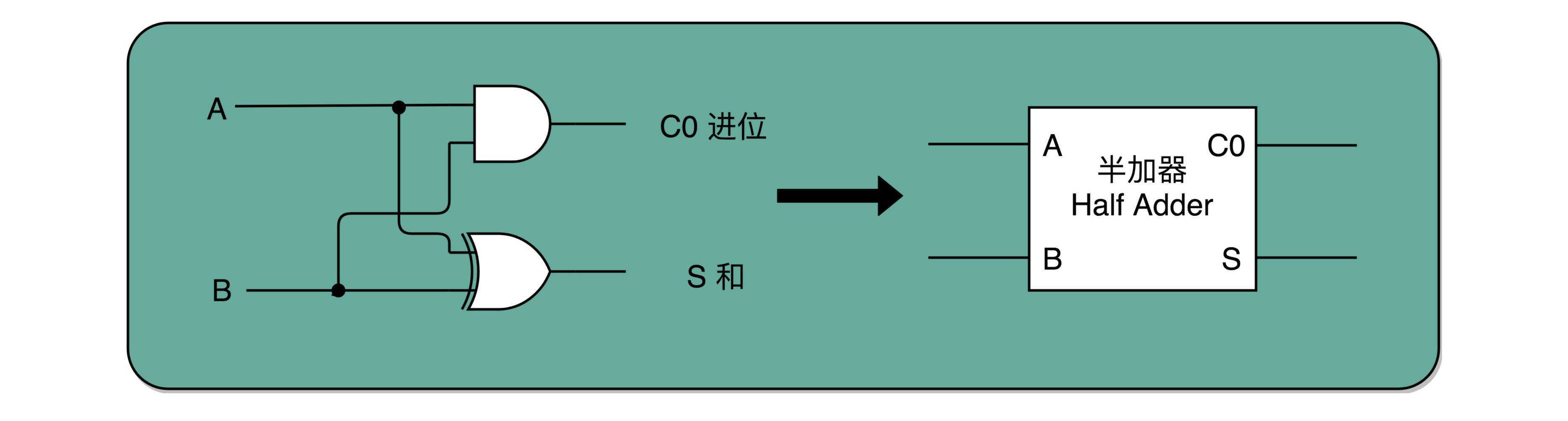
二、全加器
使用半加器,我们计算出了当前位的值和是否进位的标记,但是上一位计算时我们需要计算三个数:两个加数和一个进位数,解决方案是使用两个半加器和一个或门就可以组成一个全加器。第一个半加器得到当前位结果X和是否进位的结果Y,第二个半加器将第一步加和结果X和进位信号进行计算得到该位上结果W和进位结果V,两个半加器输出的进位信号输入一个或门就得到该位计算是否向上一位进位的信号。即使该位上三个数都是1结果也不过只进位1,所以这种电路组合完全足够使用。这样通过两个半加器和一个或门我们就组成了一个接收进位信号、加数和被加数这样三个数组成的加法,称为全加器。
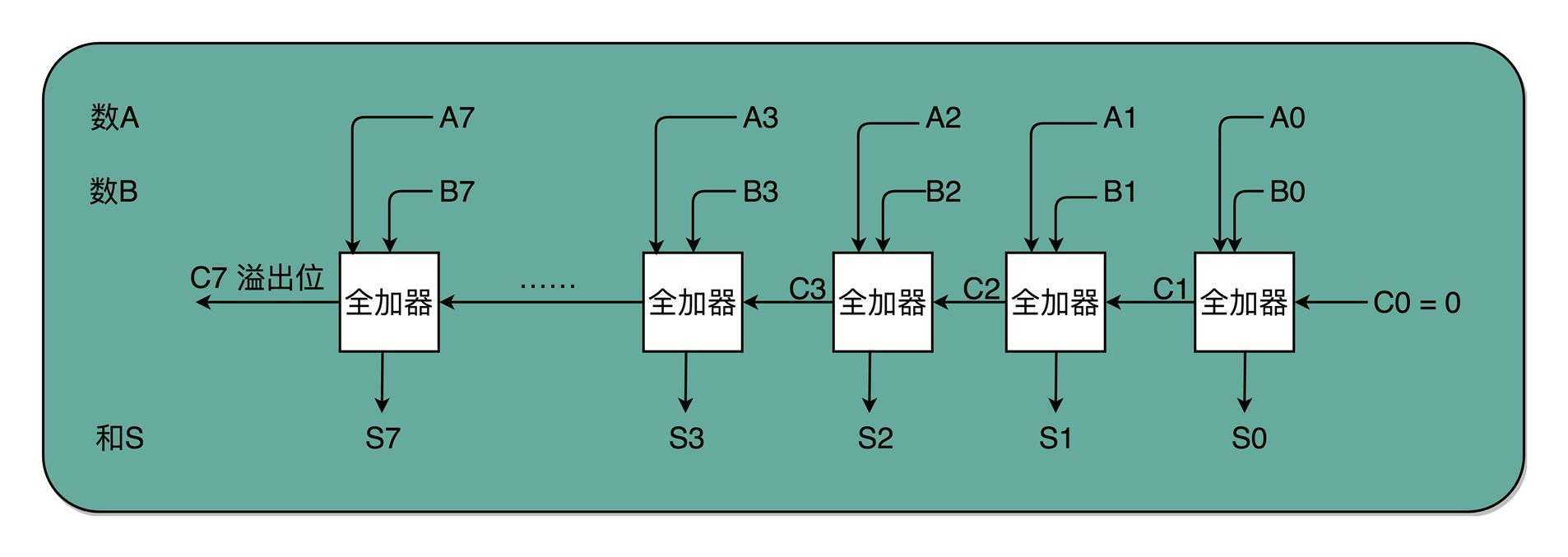
需要注意的是,这个味全加器,最低位没有进位输入,可以将其固定输入为0或只使用一个半加器即可。在最高位我们可以通过他的全加器是否有进位输出来判断计算是否有溢出。
我们吧全加器、半加器等等这样的做算数逻辑运算的组件称为ALU即算数逻辑单元,以后学习CPU设计和算数通路,以ALU为一个基础单元。
原文:https://www.cnblogs.com/rxmind/p/12829181.html