数据结构（二叉树）

二叉树

　　二叉树的定义：是n个结点的有限集合；（n>=0）特别之处在于度不能超过2；

特殊二叉树

　　满二叉树：在一棵二叉树中，所有分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上

　　满二叉树特点：

• 叶子只出现在最后一层
• 非叶子结点的度一定是2
• 在同样深度的二叉树满，满二叉树的结点个数一定最多，叶子结点也是最多的

　　完全二叉树：对一颗具有n个结点的二叉树按层序编号，如果编号为 i(1<=i<=n) 的结点与同样深度的满二叉树中编号为 i 的结点位置完全相同，则称为完美二叉树（其实就是满二叉树在最后一层叶子结点上从右到左去掉若干个结点）

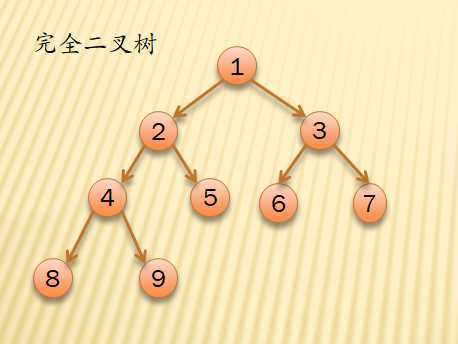
  完全二叉树特点：

• 叶子结点只能出现在最下两层
• 最下层的叶子结点一定在左部连续位置；倒数第二层，若有叶子结点，一定在右部连续位置
• 如果结点度为1，则该结点只有左孩子
• 同样结点的二叉树，完全二叉树的深度最小

二叉树的性质

• 第 i 层上最多有 2^(i-1) 个结点
• 深度为 k 的二叉树至多有 2^k-1 个结点（ 2^0+2^1+...+2^(k-1)= 2^k-1 ——等比公式）
• 叶子节点数为n0，度为2的结点数为n2，则 n0=n2+1；（叶子结点数=度为2的结点数+1）

1. 证明：结点总数为 n ，度为 0 的叶子结点数为 n0，度为 1 的结点数为 n1，度为 2 的结点数为 n2，树中连接线为 n-1；
2. n-1=n1+2*n2　　=>　　n-1=n0+n1+n2-1=n1+n2+n2　　=>　　n0=n2+1

• 具有n个结点的完全二叉树的深度为 【└ Log?n ┘+1：Log?n 取下限加1（取下限就是去除小数部分）】相应由性质2可推导出满二叉树的深度为 Log?(n+1)。

1. 证明：完全二叉树的结点数的范围在比它少一层的满二叉树和跟它同一层的满二叉树之间，所以Log?n 取下限加1

• 完全二叉树，给任意一结点 i 有：

1. 如果 i=1，为根节点；如果 i>1，则其双亲序号是结点└ i/2 ┘
2. 如果2*i>n，则结点 i 无左子结点，（连左子结点都没有就说明是叶子结点）；如果2*i<=n，则结点 i 的左子结点是 2i；
3. 如果2*i+1>n，则结点 i 无右子结点，（没有左子结点不能说明是叶子结点，应为可能有左子结点）；如果2*i+1<=n，则结点 i 的右子结点为 2i+1
4. 左子树序数都为偶数，右子树序数都为奇数

二叉树的存储结构

　　顺序存储结构：在数组中按结点编号把元素存储到相应下标中，若某下标无对应的结点序数，用空表示（遇到斜二叉树时比较消耗空间）

　　二叉链表：包括一个数据域和两个指针域

1 typedef int ElemType;
2 
3 typedef struct BirTNode{
4     ElemType data;
5     struct BiTNode *lchild;//左孩子
6     struct BiTNode *rchild;//右孩子
7 }BirTNode,* BirTree;

二叉树的遍历

　　前序：若二叉树为空，则操作返回，否则先访问根节点，再前序左子树，然后前序右子树；

　　中序：先中序左子树，再访问根节点，然后访问右子树；

　　后序：先后序左子树，再后序右子树，然后访问根节点；

　　层序：从树的第一层，从上到下逐层遍历，同层从左到右逐个访问（适用于顺序存储的访问）

数据结构（二叉树）

原文：https://www.cnblogs.com/TianLiang-2000/p/12830237.html