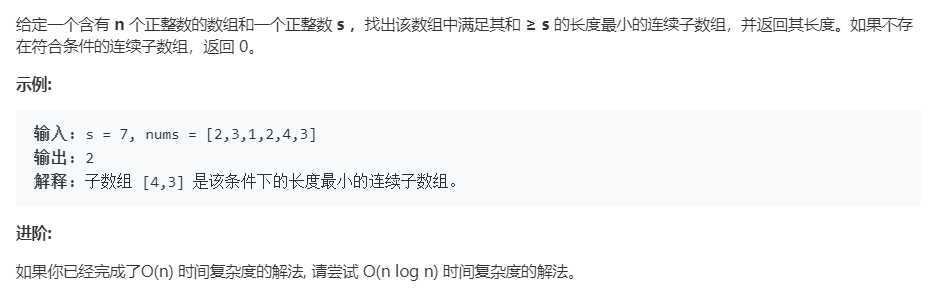
题目:
解答:
方法一:暴力法
按照题目要求直接求。把所有可能的子数组求和并更新ans ,直到我们找到最优子数组且和满足 sum≥s 。
(1)初始化ans = INT_MAX;
(2)用变量i从左到右遍历数组:
A. 用变量j从当前元素到数组尾部遍历:
a. 将i到j这些元素求和得到sum
b. 如何和sum比s大:
i. 更新ans = min(ans, (j - i + 1))
ii. 继续迭代
1 int minSubArrayLen(int s, vector<int>& nums) 2 { 3 int n = nums.size(); 4 int ans = INT_MAX; 5 for (int i = 0; i < n; i++) { 6 for (int j = i; j < n; j++) { 7 int sum = 0; 8 for (int k = i; k <= j; k++) { 9 sum += nums[k]; 10 } 11 if (sum >= s) { 12 ans = min(ans, (j - i + 1)); 13 break; //Found the smallest subarray with sum>=s starting with index i, hence move to next index 14 } 15 } 16 } 17 return (ans != INT_MAX) ? ans : 0; 18 }
方法二:双指针
用双指针left和right表示一个窗口。
(1)right向右移增大窗口,直到窗口内的数字和大于等于s,进行第(2)步;
(2)记录此时的长度,left向右移动,开始减少长度,每减少一次,就更新最小长度。直到当前窗口的数字和小于了s,回到第(1)步;
1 public int minSubArrayLen(int s, int[] nums) { 2 int n = nums.length; 3 if (n == 0) { 4 return 0; 5 } 6 int left = 0; 7 int right = 0; 8 int sum = 0; 9 int min = Integer.MAX_VALUE; 10 while (right < n) { 11 sum += nums[right]; 12 right++; 13 while (sum >= s) { 14 min = Math.min(min, right - left); 15 sum -= nums[left]; 16 left++; 17 } 18 } 19 return min == Integer.MAX_VALUE ? 0 : min; 20 }
方法三:二分查找。

1 class Solution { 2 public: 3 int minSubArrayLen(int s, vector<int>& nums) 4 { 5 int n = nums.size(); 6 if (n == 0) 7 { 8 return 0; 9 } 10 int ans = INT_MAX; 11 12 vector<int> sums(n + 1, 0); 13 //size = n+1 for easier calculations 14 //sums[0]=0 : Meaning that it is the sum of first 0 elements 15 //sums[1]=A[0] : Sum of first 1 elements 16 //ans so on... 17 for (int i = 1; i <= n; i++) 18 { 19 sums[i] = sums[i - 1] + nums[i - 1]; 20 } 21 for (int i = 1; i <= n; i++) 22 { 23 int to_find = s + sums[i - 1]; 24 auto bound = lower_bound(sums.begin(), sums.end(), to_find); 25 if (bound != sums.end()) 26 { 27 ans = min(ans, static_cast<int>(bound - (sums.begin() + i - 1))); 28 } 29 } 30 return (ans != INT_MAX) ? ans : 0; 31 } 32 };
原文:https://www.cnblogs.com/ocpc/p/12830339.html