题目:

解答:
方法一:排序。
如果对数字进行排序,则任何重复的数字都将与排序后的数组相邻。
方法二:集合。
如果我们在数组遍历时存储每个元素,我们可以在数组迭代过程中检查每个元素。
方法三:二进制
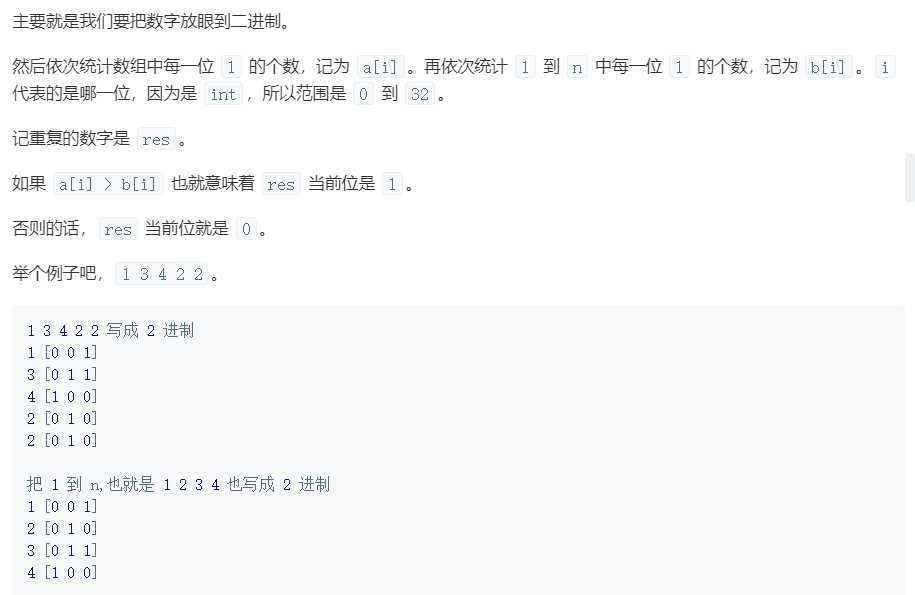
方法四:二分查找
int findDuplicate(vector<int> &nums) { int len = nums.size(); int left = 1; int right = len - 1; while (left < right) { int mid = left + (right - left + 1) / 2; int cnt = 0; for (int num:nums) { if (num < mid) { cnt++; } } // 根据抽屉原理,严格小于 4 的数的个数如果大于等于 4 个, // 此时重复元素一定出现在 [1, 3] 区间里 if (cnt >= mid) { // 重复的元素一定出现在 [left, mid - 1] 区间里 right = mid - 1; } else { // if 分析正确了以后,else 搜索的区间就是 if 的反面 // [mid, right] // 注意:此时需要调整中位数的取法为上取整 left = mid; } } return left; }
方法四:快慢指针
1 class Solution { 2 public: 3 int findDuplicate(vector<int>& nums) 4 { 5 int tortoise = nums[0]; // 慢指针 6 int hare = nums[0]; // 快指针 7 do { 8 tortoise = nums[tortoise]; 9 hare = nums[nums[hare]]; 10 } while(tortoise != hare); 11 12 // 快慢指针相遇,说明有环 13 // 注意:相交点一定是环上的点,但不一定是入口 14 15 // Find the "entrance" to the cycle. 16 // 证明:设环长度为 b,链表头到环入口举例为 a,即 [1, 2, ... a, 1(环入口), 2, ... b, z1(出环了), z2, ...]; 17 // 证明:设快慢指针在环上第 x 步时相遇,则慢指针一共走了 a + x 步,快指针一共走了 2(a + x) 步; 18 // 证明:则在环上,快指针走了 a + 2x 步,并且快指针已经走完了一圈环又回到了 x 处,即 a + 2x - b = x、得 b - a = x; 19 // 证明:故快慢指针在环上某点相交、而不一定在环入口处相交,证毕。 20 // 找到相交点后,慢指针从链表起点走 a 步可到达环入口;快指针从相交点走 a 步也会到达环入口,从而找到环入口(即重复元素) 21 int ptr1 = nums[0]; // 一个指针从链表头走 22 int ptr2 = tortoise; // 一个指针从相交点走 23 // 走了 a 步后,他们会在环入口处相遇 24 while(ptr1 != ptr2) 25 { 26 ptr1 = nums[ptr1]; 27 ptr2 = nums[ptr2]; 28 } 29 30 return ptr1; 31 } 32 };
原文:https://www.cnblogs.com/ocpc/p/12830412.html