粒子群算法

粒子群算法的启发

　 自然界中各个生物均具有一定的群体行为，人工生命主要研究任务：

1. 　　  探索自然界生物的群体行为。
2. 　　  在计算机中建立这种群体行为模型。

  群体中每个个体具有非常简单的行为规则，但是群体中行为规则却是极其复杂。群体行为可以由以下三种规则进行建模：

1. 　　飞离最近的个体，以避免碰撞
2. 　　飞向目标
3. 　　飞向群体的中心

　 鸟类寻找栖息地和特定问题寻找解类似，已经找到栖息地的鸟引导它周围的鸟飞向栖息地，增加整个鸟群找到栖息地的可能性。

扩展内容

　 Craig Reynolds 于1986年制定了一套有序的动物集群运动（如鸟群、鱼群）的计算模型。该模型基于计算机动画或计算机辅助

设计的计算机三维几何。他将这种模拟鸟群命名为boids。

　　BOIDS这个词是"bird-oid object"这几个词的缩写，指的是鸟类动物。Boids是一个研究”涌现“现象的例子。即：Boids的复杂

性来自能动个体单元（Agent，即这里的Boids）间根据简单的的互动法则而产生的系统结构特性。在这个模型中，每个个体的行为只

和它周围邻近个体的行为有关，每个个体只需要遵守三条规则：

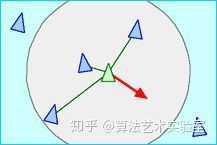
  飞离最近的个体，以避免碰撞   

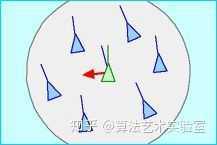
  和邻近个体的平均速度保持一致 

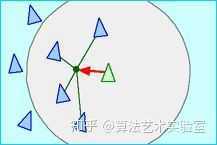
   向邻近个体的平均位置移动

粒子群算法

　　就我个人而言，上面的内容不足以让我对粒子群算法有所了解，反而让我对粒子群算法产生了敬畏之心。我觉得只是就是言简意赅，

让普通大众都能接受。这就是我写这篇文章的目的。

　  下面是我对这图的解释：

　 从前，A和B是一对好朋友，他们相约测量湖的深度。

模型假设

• A、B各有一条船和一个测量工具
• 上图是假设为湖的一个切平面
• 他们事先不知道湖水那块最深
• index_i表示船的位置；A_value_i表示i位置湖水的深度

操作过程

1. 交流 ：将A位置湖水的深度(粒子群算法中的适应度值)和B位置湖水的深度进行比较
2. 学习：如果 A位置湖水的深度 > B位置湖水的深度，那么将B位置的船儿向前划行一个步长，否则，将A位置的船儿向前划行一个步长。

　　经过上面的解释，你一定会想这和粒子群有啥关系呢？有这种想法的同学，我个人觉得你对粒子群的理解还在表面。在我研究粒子群算法的时候，

让我纠结的是，它那两个迭代公式。下面让我们探究一下粒子群算法的理论知识：

设

X_i = (x_i1,x_i2,...,x_in)  为微粒 i 的当前位置。

V_i = (v_i1,v_i2,...,v_in)  为微粒 i 的当前飞行速度。

P_i = (p_i1,p_i2,...,p_in)  为微粒 i 所经历的最好位置，也就是微粒 i 所经历过的具有最好适应度位置，称为个体最好位置。

　　为了讨论方便，设f (X) 为最小化目标函数，则微粒 i 的当前最好位置由下面式子决定：

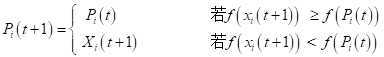
　　设群体中的微粒数目为s，群体中所有微粒所经过的最好位置为P_g(t)，称为全局最好位置。则

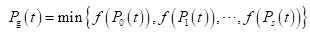
　　根据上面的定义，基本粒子群算法的进化方程：

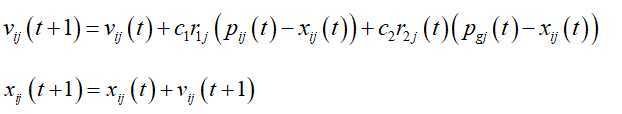
其中，下表j表示微粒的第j维，i表示微粒i，t表示第t代，c_1、c₂为加速常数，通常在0—2之间取值，r₁,r₂是0—1之间相互独立的随机数。

　　下面我用几何图形来解释这两个公式：

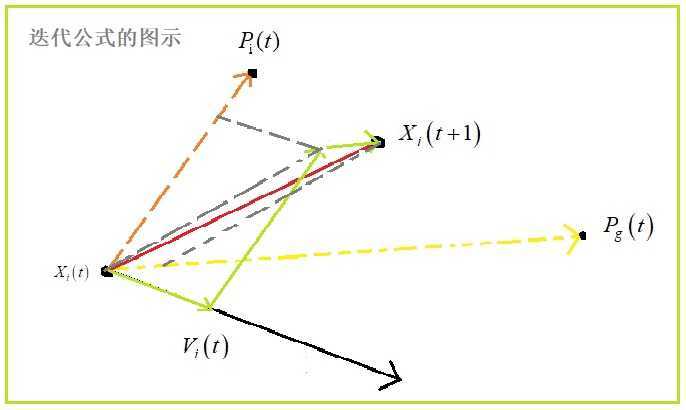
　　我觉得流程图没必要画了，有以下原因：

　　电脑没有装专业画图软件

　　网上都能找到相关的知识

　　对这方面有兴趣，同学可以加一下QQ群：1073469607 ，加群的目的：相互交流，不会的可以问群里面的大佬。

粒子群算法

原文：https://www.cnblogs.com/mysterygust/p/12831697.html