对于复数域的矩阵A, (n阶），应当明白这个矩阵的特征多项式（n次）一定是有n个解的，那么就有以下的结论：
如果对矩阵A有一个特征值λ0，对应其特征向量α，
有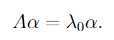
，那么可以推出
。
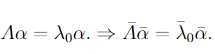分解A = B + Ci， α = β + γi， 定义A，B， C中元素用a, b, c,表示， α， β， γ的坐标对应分量用x， y， z 表示；
于是就有： aij = bij +cij * i; xj = yj + zj * i; 那么就有对于任意的A和α， 针对复数域上的计算，有Aα = （∑a1j*xj, ∑a2j*xj, ……， ∑anj*xj） = ( ∑(b1j + c1j*i)(yj + zj*i), ……∑(bnj + cnj*i)(yj+zj*i)), 不难看出把上面的式子中的加号变成减号，我们可以发现一个比较有用的结论 :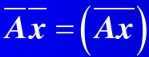
, （一个矩阵的共轭）乘上（一个向量的共轭）等于（
这个矩阵乘上这个向量）的共轭 那么对于上面的式子A α = λ0 * α，有同时对左右进行共轭运算（共轭可以看成是一个映射或者函数），则有了这样的结论。（把λ0看成λ0乘上单位矩阵I）。
又有若A为实数矩阵的话，有A等于A的共轭，那么就可以看到一个实数矩阵如果有一个复数特征值，那么其共轭值也是A的特征值，两个共轭特征值的特征向量也共轭。
注：这里矩阵和向量的共轭都是指把虚数部分的系数取相反数。
欧式空间是定义了夹角和内积的线性空间。
定义内积为一个线性空间V到数k的函数， （α， β）= α·β = α * β^T , (乘法是矩阵乘法，点乘是内积）
正交矩阵也有定义： 若有A*AT = I ， 那么A即为正交矩阵，正交矩阵的行向量组和列向量组都是单位正交向量组，且线性无关。
正交：（α， β） = 0， 两者正交。
因为标准正交基总是便于我们进行一些计算，（比如平面和立体直角坐标系）， 我们总希望把映射定义在一个标准正交基上，于是总希望找到正交相似的对角矩阵，这个矩阵不仅能够满足我们对描述映射的简单化，更能够使得对应的这些特征向量
求正交矩阵比较好的办法，先通过特征值找到特征向量，然后用特征向量进行施密特正交化（Schmidt），如果是对称矩阵，则对其中不同的特征值下的特征向量组分别进行正交化即可.
有几个结论： 1. 实对称矩阵一定有n个实数特征值
2. 实对称矩阵属于不同特征值的特征向量一定是正交的
3.实对称矩阵一定正交相似于对角矩阵
双线性函数：定义在V*V 到数域K的映射（函数），若有对任意的α，β，γ属于V， f（α，kβ+γ）=k*f（α，β）+f（α，γ）， f（kα+γ， β）= kf（α，β）+f（γ， β），（对两个分量都是线性映射的关系）
则f为一个V*V上的双线性函数，由于线性空间和线性映射的特性，一个双线性函数完全V的基向量所决定。
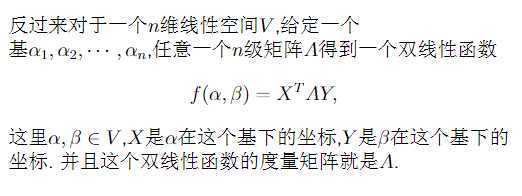
注：这里的X和Y由于是坐标，他们一定是列向量，也就是说X^T * A * Y最终得到的是一个1*1的函数，行向量乘矩阵乘列向量最终得到了一个数（函数）而不是函数矩阵，这里要千万注意。
和映射一样，同一个双线性函数可能有不同的度量矩阵，表示的是同一个函数（也就是说对两个向量α， β，尽管两个坐标可能发生变化，但是这两个向量作为自变量是不变的，所以函数值事实上也不会变）
证明思路： 对任意两个个向量分别用两个基来表示求对应的矩阵。可以得出定理。
要分清坐标向量和映射对应矩阵的左乘右乘！（重点就在于不同的坐标表示相同的向量，也就表示了相同的函数）
将合同与相似类比，就发现双线性函数也就是一种映射。
P：对任意β，f（α1，β）=0.
Q： 对任意α， f（α，β1）=0
满足p的所有α1构成的集合称为f的左根， radL f
满足q 的所有β1构成的集合称为f的右根，radRf
如果f的左右根都是零子空间，那么f就称为非退化的，就是仅有零的左根和右根，可以类比可逆矩阵（非奇异矩阵）
度量矩阵可逆，则f非退化。
证明提示：只考虑对V的基α1到αn的双线性函数的处理， 即定义一个基α1~αn，对应的有f（αi ， αj） = f（αj， αi），所以得证。
原文：https://www.cnblogs.com/zy1120192493/p/12829811.html