目录
一、从二叉树说起
二叉树的介绍
二叉树结点删除
存在的问题
二、红黑树
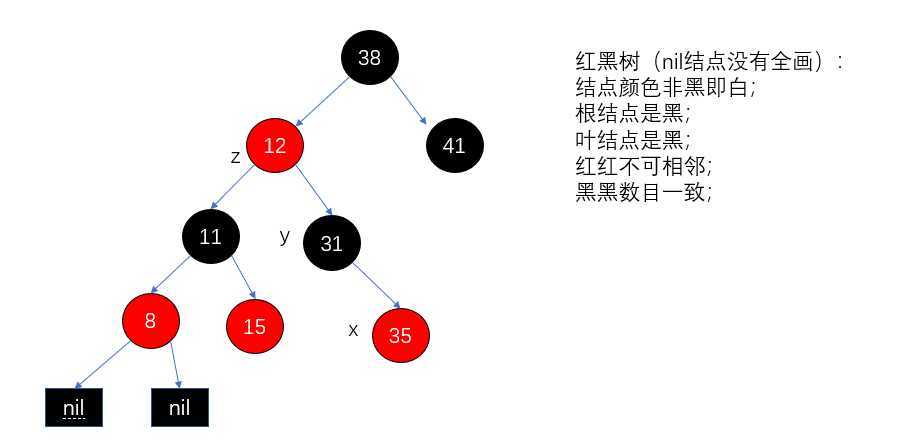
定义
红黑树插入
红黑树删除
三、红黑树的应用
动态序问题
从二叉查找树说起
用途:查找某个给定的值,在最好情况下的时间复杂度是O(lgn)级别的,注意是最好;结点的插入和删除,时间复杂度也是O(n);
问题是:当插入的序列基本有序,可以是正序,也可以是倒序,这个时候二叉树的高度上升到O(n),查找、插入、删除的时间复杂度都是O(n);
所以就出现了二叉平衡树和红黑树的变种,动态地维护树形,避免出现极端情况。
二叉查找树的查找、插入、删除
查找和删除可以理解为一个动态查找,找不到就插;
删除比较复杂:
1)叶结点,直接删除;
2)非叶结点,只有左子树或右子树,用子结点代替待删除结点即可;
3)非叶结点,既有左子树又有右子树,这种情况比较复杂:
我们假设:z表示待删除结点,y表示实际被删结点,x表示拼接结点,这里就是y的子结点
找它的后继结点y,这里也可以是前驱结点,先删除y(当然要事先保留y的值),再用y的值替换x的值即可。
注意:y要么是一个叶结点,要么是一个只有右子树的结点,这是由二叉树的性质来决定的。
完整的删除原码见github:
红黑树的插入:
先按照二叉查找树的思路插入,必然是作为叶结点插入,而且默认是红色。性质4会遭到破坏,因此围绕着性质四来展开修复工作。
这里有个问题,为什么是作为红色结点插入,而不是黑色结点?
插入黑结点会导致性质5遭到破坏,会导致全局范围内的黑高度不一致。
插入的四种情况:
直接结合源代码来解释,原码来自算法导论第二版:
RB-INSERT-FIXUP(T,z) while(z.p.color == RED)//循环的出口是z的父节点为黑色 //插入结点位于祖父结点的左子树 if z.p == z.p.p.left //y是叔父结点 y = z.p.p.right //叔父结点是红色,对应情况一 if y.color = RED z.p.color = BLACK y.color = BLACK z.p.p.color = RED z =z.p.p //叔父结点不存在或者是黑色,而且z位于父节点的右子树,对应情况二,转为情况3(左右转为左左) else if z == z.p.right z = z.p LEFT-ROTATE(T,z) //进入情况3 z.p.color = BLACK z.p.p.color = RED RIGHT-ROTATE(T,z.p.p) else(same as then clause with "right" and "left" exchanged) //最后要把根结点置为黑色 T.root.color = BLACK;
插入操作时间复杂度分析:
要明确:左旋或右旋操作,都是局部性的元素变换,它的时间复杂度是常数;
第一步是插入操作,寻找插入位置,走的是从根到叶结点;
第二步是颜色的调整,走的是从叶结点到根,即一个while循环。
所以最坏情况下的时间复杂度可以看作O(2lgn),即O(lgn)
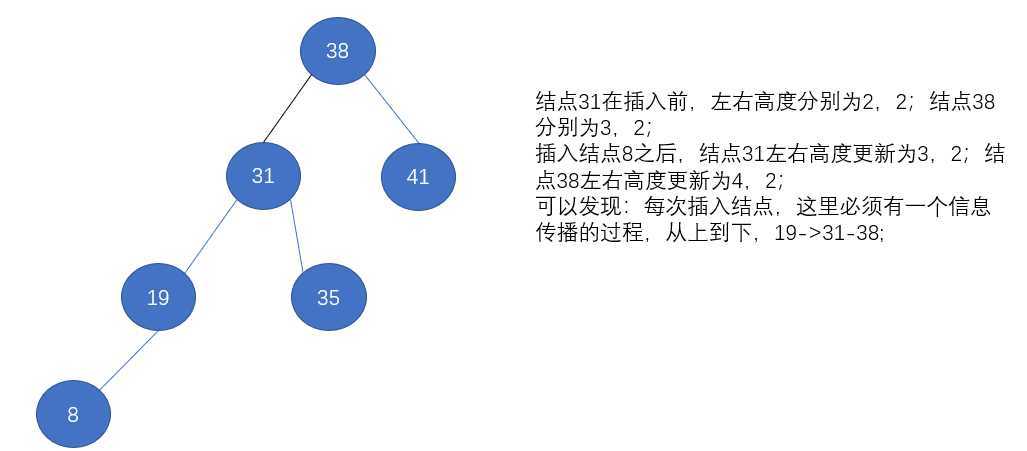
41 38 31 12 19 依次插入红黑树,过程如下:
插入41:

插入38:

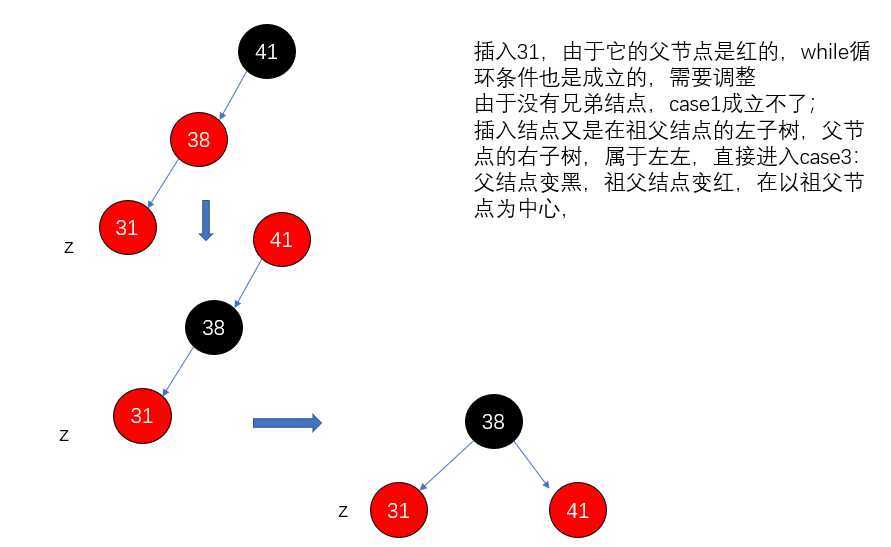
插入31:
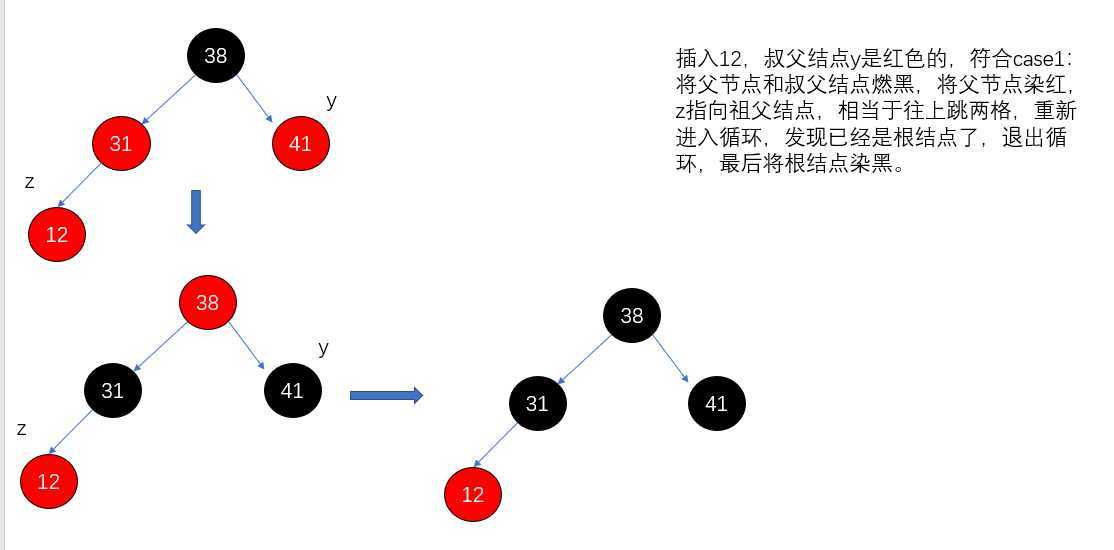
插入12:
插入19:
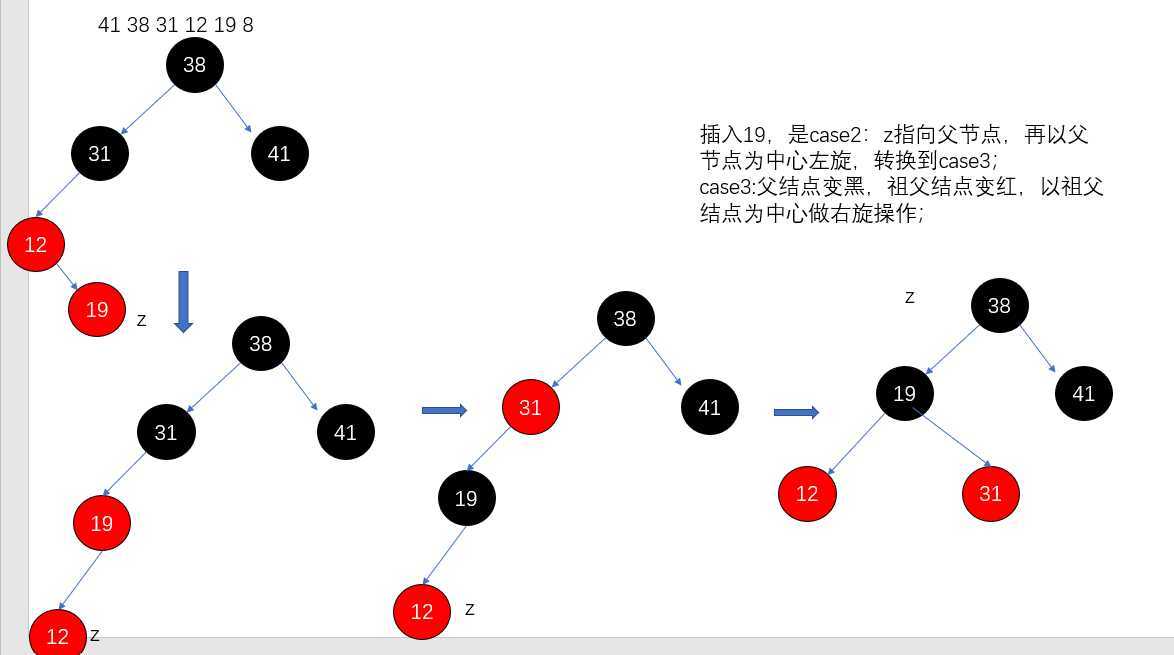
红黑树的删除
1)如果删除的是叶结点,没啥动作;
2)如果删除的是非叶结点,而且y的颜色是黑色
1)如果z结点只有一个孩子,则y等同于z,直接用x结点代替y结点,再进行颜色的调整。
2)如过z结点有两个孩子,则用y结点的值代替z结点的值(仅是值替换),然后用x结点代替y结点(这里就有颜色的变换了)。所有相当于是删除了y结点。那么就涉及到以结点x为中心的颜色跳整动作,x是拼接结点。
如果y的颜色是红色则不需要调整,原因很明显,如果y是黑色,y被x所替换,性质4和性质5都有可能遭到破坏;
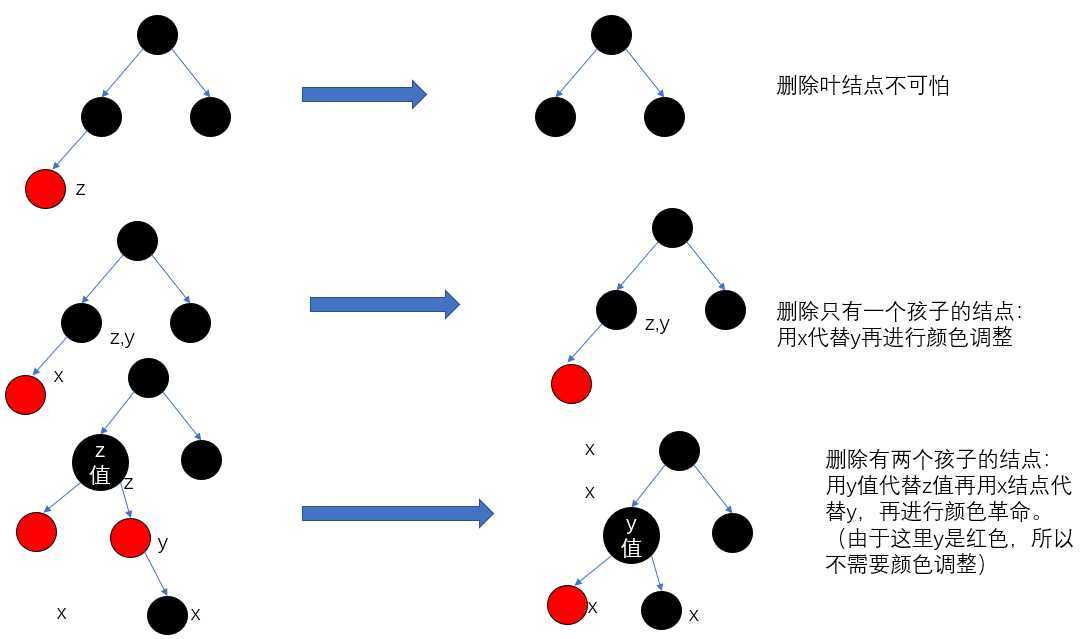
调整的 情况有分为四种,每种各有不同的处置策略,看源代码:
//x是根结点或者x的颜色为红色则停止调整 while x != T.root and x.color == BLACK //讨论的是x是父节点的左子结点的情况 //w是x的兄弟结点 if(x == x.p.left) w = x.p.right; //兄弟结点是红色,进入情况一,转入情况二三四 //这一步操作的目的在于将w调整为黑色 if w.color == RED w.color = BLACK x.p.color = RED LEFT-ROTATE(T,x,p) w = x.p.rigth //兄弟结点是黑色而且兄弟结点的左右子节点都是黑色,进入情况2(黑黑) if w.left.color == BLACK and w.right.color == BLACK w.color = RED; x = x.p; //兄弟结点是黑色,它的右子结点是黑色,进入情况3,转入情况四(?黑,?代表左子结点既可能不存在,也可能是红色,即不关注左子结点) //这一步操作将右子结点要转变为红色 else if w.right.color == BLACK w.left.color = BLACK; w.color = RED; RIGHT-ROTATE(T,w); w = x.p.right; //进入情况四,左子结点是红色(?红,?代表左子结点可能是不存在、黑色、红色,即不关注左子结点) w.color = x.p.color; x.p.color = BLACK w.right.color = BLACK; LEFT-ROTATE(T,x,p); x = T.root; else (same as then clause with "right" and "left" exchanged) x.color = BLACK
情况一是一个过渡状态,会转换到二三四;
情况二回导致x上移一格,x = x.p
情况三也是过渡状态,会转换到四;
情况四是一种终结状态;
删除操作时间复杂度分析:
同插入操作,是O(lgn);
数据结构扩张:
要解决某一个问题,而基础的数据结构无法满足问题的求解需要,并不需要新创建一个新的基础数据结构,而是选择一个合适的、原有的基础数据结构,通过添加额外的信息和规则,来创建一个复合数据结构,从而到达求解问题的目的。而且要注意:原有数据结构的性质不能变。
题外话:二叉树到红黑树可以看作是数据结构的扩张。为了控制树的高度,在二叉树中加入了额外的存储信息,即结点的红黑颜色,还有一系列规则。红黑树的插入和删除,是在二叉树插入和删除的基础上,通过FIX-UP函数,保证红黑性质不被破坏。
如何扩张一个数据结构:
1)选择一种基础数据结构;
2)确定基础数据结构中要维护的附加信息;
3)检验基础数据结构上的基本修改操作能否维护附加信息;(难点)
4)设计一些新操作。
定理:对红黑树进行数据结构扩张,必须满足如下要求:结点的额外信息必须唯一依赖:1)结点本身;2)左子结点额外信息;3)右子结点额外信息;这样就能够保证:原有红黑树的插入和删除操作仍然可以满足O(lgn)级别的时间复杂度。否则,为了维护额外信息,可能会付出高于o(lgn)级别的时间,红黑树的性质就遭到了破坏。
动态顺序统计问题
解决的问题:求一个排列中,某个特定结点的序,要求在O(1)时间复杂度内完成,而且这个排列是动态的,即不断有数据插入和删除。
解决方案:
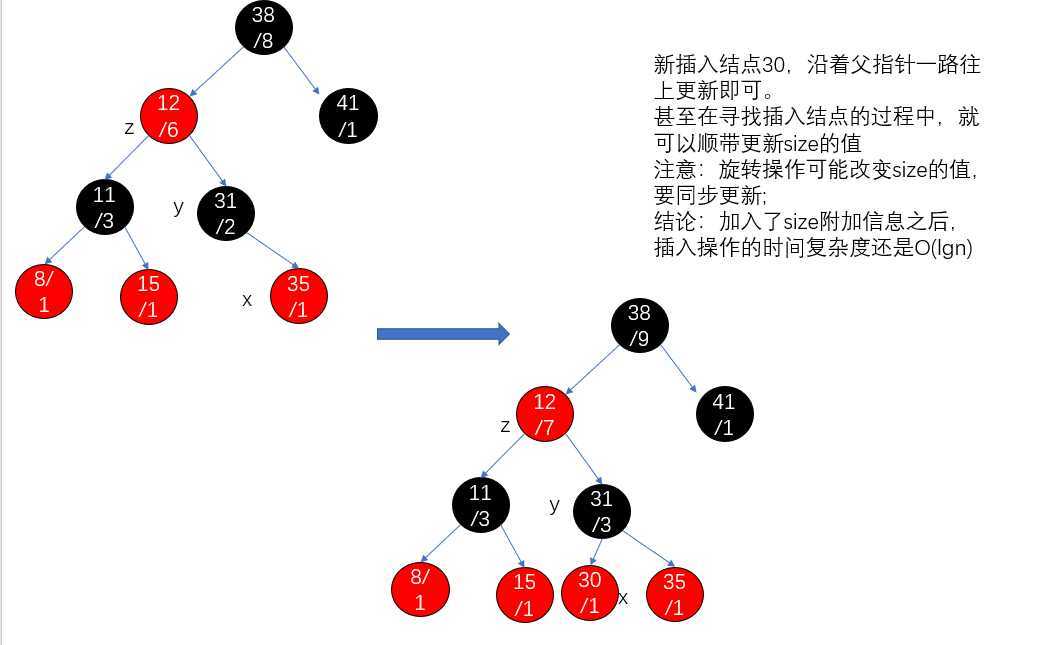
利用红黑树,结点的存储结构如下:

如何保证插入一个结点,时间复杂度是O(lgn):
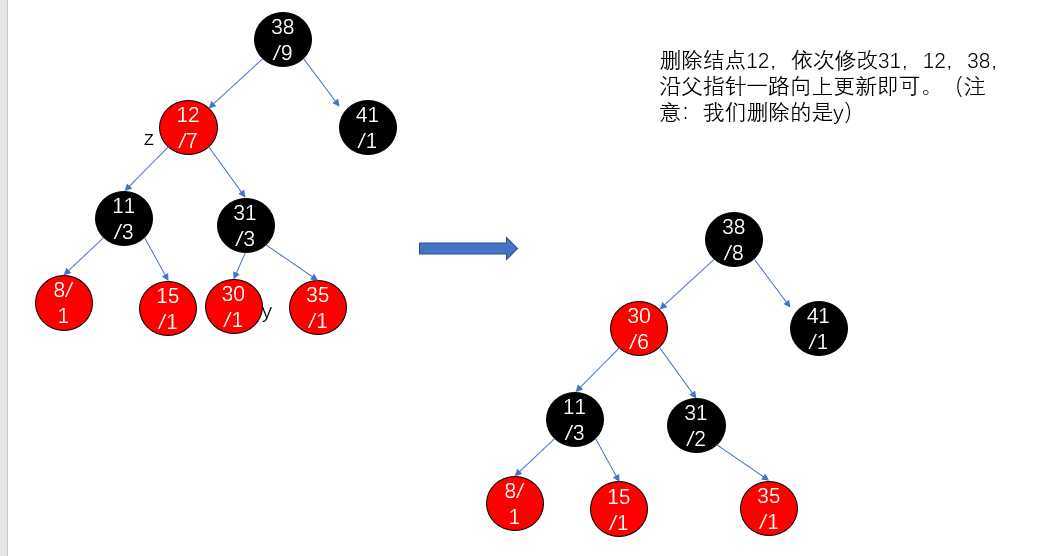
删除一个结点基于同样的道理:
现在来回答提出的问题——给定一个结点,如何查找它对应的序:
OS-RANK(T,x) r = r.left.size+1; y = x; while(y != T.root) //关键一步:如果y是父节点的右孩子,则x的排名要考虑父节点和父节点中的左子结点,相加 if(y == y.p.right) r = r+y.left.size+1; y = y.p; return r;
反过来,给定一个序,如何查找到对应的结点:
OS-SELECT(x,i) r = x.left.size+1; if i == r return x; else if i < r //如果进入左子树,序不变,如果进入右子树,序变为i-r return OS-SELECT(x.left,i); else return OS-SELECT(x.right,i-r); //非递归形式 OS-SLECT(x,i) p = x; while p != NIL r = p.left.size+1; if i == r return p; else if i < r p = p.left; else p = p.right; i -= r;
动态序问题完美解决!
原文:https://www.cnblogs.com/chxyshaodiao/p/12837710.html