这里的加入是把每个元素看成一个集合!!!
这道题主要是讲一下整体二分。
整体二分顾名思义,就是有一坨数,规定一个 \(mid\) 进行二分。(好像一点也不清楚)
思考一下普通的二分,我们其实是帮助一个数值 \(ans\) 选择一个合适的值。整体二分就是帮助很多个数值选择一个合适的值。
接下来说一下算法流程了吧。
我们定义两个序列 \(L\) 与 \(R\)。对于此题我们的 \(mid\) 就是假定第 \(C\) 大的数,那么对于这次遍历大于 \(mid\) 的数就是能对结果产生影响的,设目前为止大于 \(mid\) 的数的个数为 \(num\)。
首先我们的时间戳是有序的,这个就不用排序了。对于每个询问与插入,我们可以进行分类讨论。
操作为询问,\(num\) 小于询问要求的 \(C\)。这说明我们把 \(mid\) 的值调大了,我们将 \(C\) 减去 \(num\),再在 \([l,mid]\) 中选择新值(即插入 \(L\))。(注意这里的 \(mid\) 是可以取到的,因为判断条件是 \(num < C\))
操作为询问,\(num\) 大于等于要求的 \(C\)。我们先前判断用的是严格大于才加入树状数组,所以等于的情况不会触及 \(mid\)。从 \([mid+1,r]\) 中找就行了。
操作为插入,\(C>mid\)。这种权值插入 \(R\),再在树状数组中更新就行了。
操作为插入,\(C<=mid\)。这种权值不满足条件,只能与第一种操作进行配对,插入 \(L\) 就行了。
看到树状数组也许你看不懂(当然你可以写线段树,比树状数组好理解得多,我是因为我是 \(250\) 才会去做的 \(QwQ\)),接下来我会详细讲解树状数组,如果没有看懂可以私信或评论哟!(蒟蒻求赞)
先来一张图:(这个可以结合代码观看,这个部分感觉网上有些代码可能有问题就比如我看的那份树状数组代码)
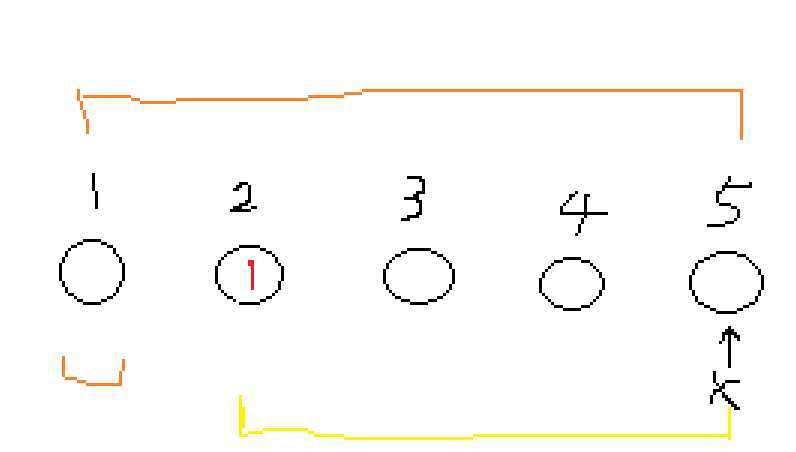
我们在 \(2\) 这个节点加了 \(1\) 这个数值,用另一个数组加了 \(2-1==1\) 这个数值。
接下来假设我们 \(ask(x==5)\)。因为这相当于是一个前缀和:对于 \(c1[]\),记录的就是在 \([1,x]\) 之间有多少个添加的 \(1\)(注意这里也可以改成 \(-1\),这个部分我就不讲了,一通百通)。而对于 \(c2[]\),记录的就是每个位置上被添加的次数 * (位置 - 1)。(注意这里的两个数组已经完成 \(ask\) 中的累加)
那么 \(\sum c1*x-\sum c2\) 对应在图上就是一条长的橙色的线段减去短的橙色的线段,正好就是黄色的线段:这个 \(1\) 到 \(x\) 的距离。
总结一下:这个 \(ask\) 函数返回的值就是 \(x\) 与之前每个位置的距离 * 这个位置被添加 \(1\) 的个数。
好的我们再放一张图,来解释最终的答案。
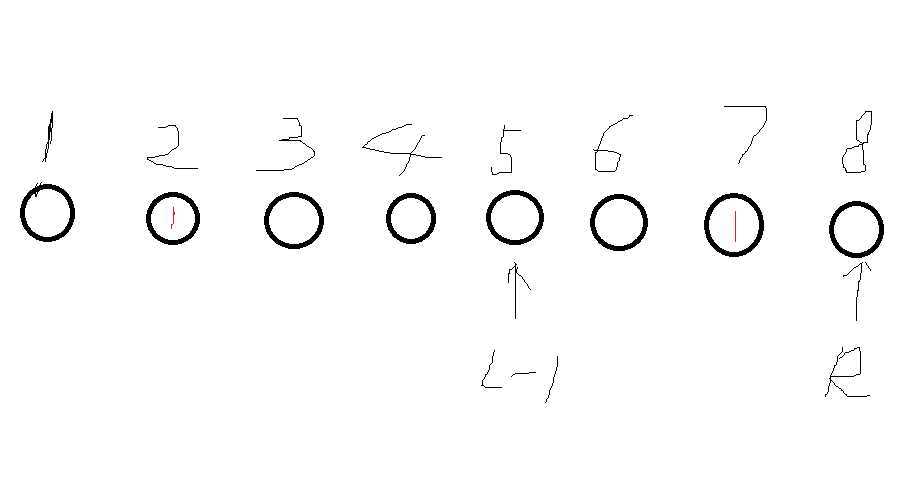
\(ask(L-1)=5-2+1=4\),\(ask(R)=(8-2+1)+(8-7+1)=9\)。
相减即为所求:在 \([L,R]\) 区间内大于 \(mid\) 的数的个数。
我竟然写完了 \(QwQ\)。(希望不要被布布扣转载小声哔哔)
#include <cstdio>
#define int long long
const int N = 5e4 + 5;
int n, m, p[N], ans[N], op[N], l[N], r[N], c1[N], c2[N], c[N], lef[N], rig[N];
int read() {
int x = 0, f = 1; char s;
while((s = getchar()) < ‘0‘ || s > ‘9‘) if(s == ‘-‘) f = -1;
while(s >= ‘0‘ && s <= ‘9‘) {x = (x << 1) + (x << 3) + (s ^ 48); s = getchar();}
return x * f;
}
int lowbit(const int x) {return x & -x;}
void add(const int x, const int k) {
for(int i = x; i <= n; i += lowbit(i))
c1[i] += k, c2[i] += k * (x - 1);
}
int ask(const int x) {
int r = 0;
for(int i = x; i; i -= lowbit(i))
r += c1[i] * x - c2[i];
return r;
}
void cdq(const int L, const int R, const int down, const int up) {
if(L > R || down > up) return;
if(down == up) {for(int i = L; i <= R; ++ i) ans[p[i]] = up; return;}
int mid = up + down >> 1; int lenl = 0, lenr = 0;
for(int i = L; i <= R; ++ i) {
int pos = p[i];
if(op[pos] & 2) {
int num = ask(r[pos]) - ask(l[pos] - 1);
if(num < c[pos]) lef[++ lenl] = pos, c[pos] -= num;
else rig[++ lenr] = pos;
}
else {
if(c[pos] > mid) add(l[pos], 1), add(r[pos] + 1, -1), rig[++ lenr] = pos;
else lef[++ lenl] = pos;
}
}
for(int i = 1; i <= lenl; ++ i) p[L + i - 1] = lef[i];
for(int i = 1; i <= lenr; ++ i) {
p[L + i + lenl - 1] = rig[i];
if(op[p[L + i + lenl - 1]] & 1) add(l[p[L + i + lenl - 1]], -1), add(r[p[L + i + lenl - 1]] + 1, 1);
}
cdq(L, L + lenl - 1, down, mid); cdq(L + lenl, R, mid + 1, up);
}
signed main() {
n = read(), m = read();
for(int i = 1; i <= m; ++ i)
p[i] = i, op[i] = read(), l[i] = read(), r[i] = read(), c[i] = read();
cdq(1, m, -n, n);
for(int i = 1; i <= m; ++ i)
if(op[i] & 2) printf("%lld\n", ans[i]);
return 0;
}
原文:https://www.cnblogs.com/AWhiteWall/p/12836999.html