@(知识点汇总)
Booth算法的原理其实小学初中就学过,比如下面这道题:
简便计算:\(8754 \times 998 = ?\)
随便抓个娃娃来都知道应该这么算:
\(8754 \times 998 = 8754 \times 1000 - 8754 \times 2\)
我们都知道在十进制里,10的倍数的乘法很容易,就是后面加几个0的事情,而上面这种简便计算都有个特点,就是会有999,1001,997,1002这种数,0和9出现的次数很多,这样就可以通过变为化简变为简单的乘法和加减法。
对于二进制数,这种简便计算的情况往往更多。因为计算机中为了计算方便,往往将数据转换为补码的形式,而补码形式在计算时会扩展符号位,比如有符号数补码5‘b10110 = -10,在计算与一个8位数相加时会扩展为8‘b11110110,可以发现,这种数往往会有很多连续的1出现,这跟上面的简便计算的例子非常相似。比如:
这就是booth算法分解乘数的基本原理。
假设A和B是乘数和被乘数,且有:
最后的Val(A)的表达式实际上就是补码A表示的原码。
上面的公式推导了booth乘法对乘数的分解原理,实际上在编码时只需要公式3,可以做如下的编码表:
| \(a_i\) | \(a_{i-1}\) | \(a_{i-1}-a_i\) | 操作 |
|---|---|---|---|
| 0 | 0 | 0 | 无 |
| 1 | 0 | -1 | 减B |
| 1 | 1 | 0 | 无 |
| 0 | 1 | 1 | 加B |
举个栗子:
\(N=7, B = 22 = (0010110)_2,A=-34=-(0100010)_2\)
首先计算-B的补码(算法中要用到):\(\overline{-B} = (1101010)_2\)
以及A的补码:\(\overline{A} = (1011110)_2\)
硬件计算过程如下:
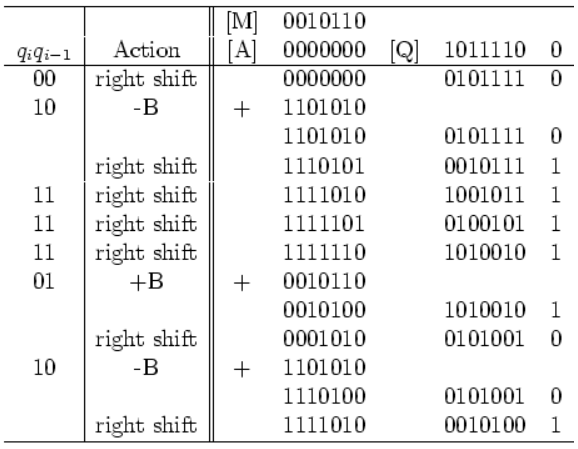
首先初始化p空间:\(p=2N+1\).[A]和[Q]是两个寄存器。其中[Q]是N+1位的。
最后的结果11110100010100就是结果的补码,也就是:
\(B\times A = \overline{11110100010100} = (10001011101100)_原 = -748_{10}\)
算法跟公式的匹配:
实际上,对于公式中的每一项\((a_{i-1}-a_i)\times B\times 2^i\)都对应实际算法中的每一步。\((a_{i-1}-a_i)\)决定了B的系数,右移操作因为作用在[A][Q]寄存器上,所以实际上是相当于将积右移,等价于B左移,所以这一步对应\(\times 2^i\)操作。加减B的操作都作用在[A]寄存器上,保证了\(\times 2^i\)后的B能够作用在正确的位上。
原文:https://www.cnblogs.com/lyc-seu/p/12842399.html