据说著名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决?Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。(这里我们将所有人杀死)
理解起来比较容易,但是代码部分有细节需要考虑(当first指向的结点出列后,具体见下面代码分析)
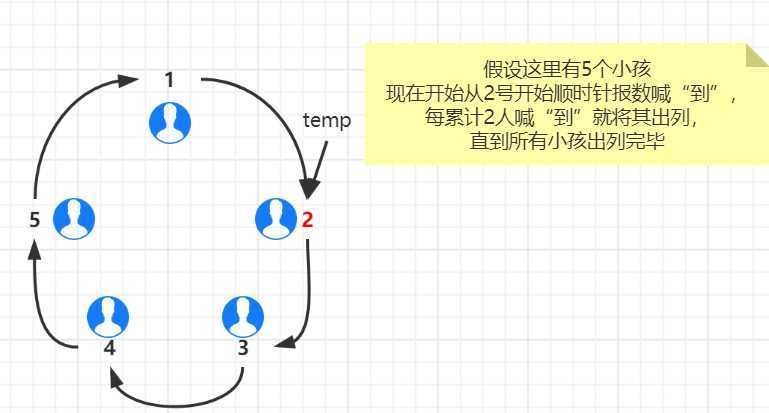
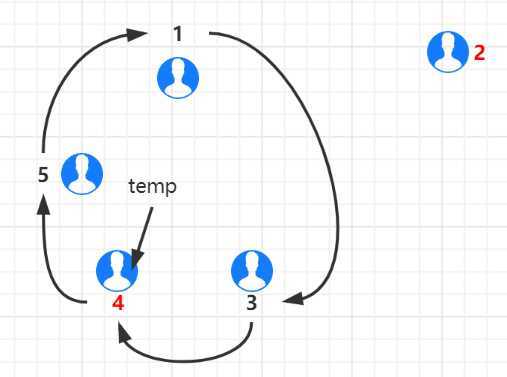
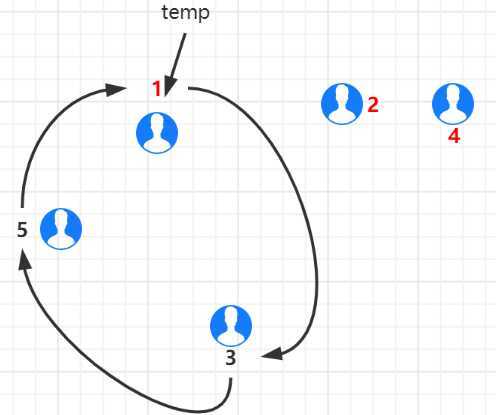
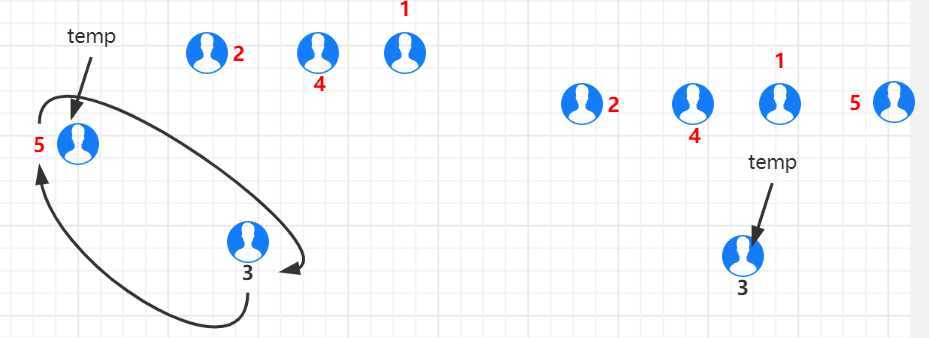
最终得到出列小孩依次为 2、4、1、5、3
首先构建约瑟夫环(即循环单链表)
1 private Boy cur=null;//这个辅助引用,代替头结点来完成循环链表的构建 2 private Boy first=null;//头结点 3 public void addBoy(int nums) {//传入多少人数 4 if (nums < 2) { 5 System.out.println("人数不得小于2人"); 6 return; 7 } 8 for (int i = 1; i <= nums; i++) {//遍历创建小孩结点 9 Boy boy = new Boy(i); 10 if (i == 1) { 11 first = boy;//将第一个结点赋给first 12 first.setNext(first);//形成一个环 13 cur = boy;//代替头结点完成接下来的链表构建 14 } 15 cur.setNext(boy);//连接新结点 16 boy.setNext(first);//形成环 17 cur = cur.getNext();//准备连接下一个结点 18 } 19 cur = cur.getNext();//让cur回到头结点处,以便后序操作 20 }
链表已经构建完成,接下来实现约瑟夫环(思路如下图):
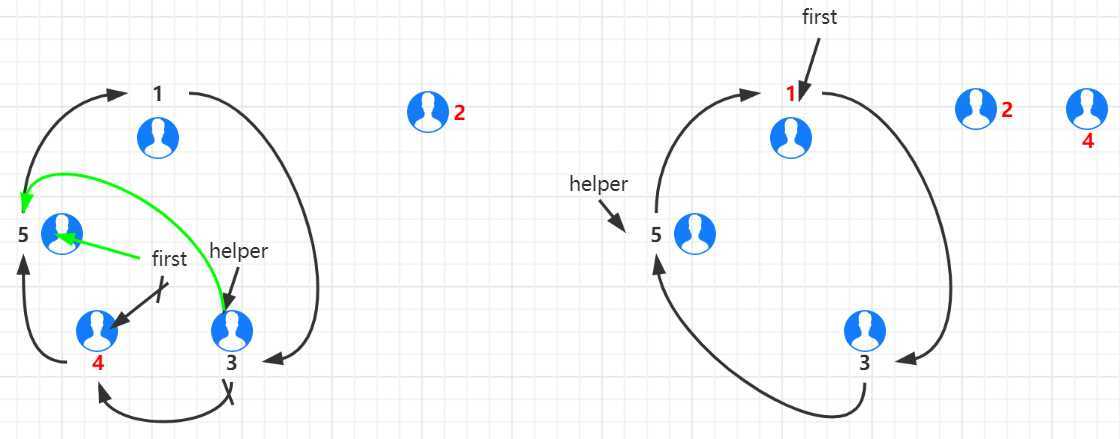
约瑟夫环核心代码:
1 /* 2 * start:从第几个小孩开始报数 3 * m:报数从first为1开始累计m人,则第m人出队,然后继续循环 4 * nums:一共nums个小孩 5 * 6 * 比如有编号为1,2,3,4,5个小孩,start为1,m为2. 则出队顺序为:2,4,1,5,3 7 */ 8 public void countBoy(int start, int m, int nums) { 9 addBoy(nums); 10 11 Boy helper = first; 12 13 while (true) { 14 if (helper.getNext() == first) 15 break; 16 helper = helper.getNext(); 17 } 18 // 从start开始报数 19 for (int i = 1; i < start; i++) {//重置头结点至start处 20 first = first.getNext(); 21 helper = helper.getNext(); 22 } 23 while (true) { 24 if (helper == first) { 25 break; 26 } 27 System.out.println("出队编号为" + first.getNo()); 28 first = first.getNext();//重置头结点为出列结点的下一个结点 29 helper.setNext(first);//之前first的后一个结点helper不再指向出列的结点,指向头结点 30 for (int i = 1; i < m; i++) {//此处要注意上面已经喊过一次“到”,这里少一次即可 31 helper = helper.getNext(); 32 first = first.getNext(); 33 } 34 } 35 System.out.println("出队编号为" + first.getNo()); 36 37 }
原文:https://www.cnblogs.com/taichiman/p/12843744.html