Ridge regression 通过对系数的大小施加惩罚来解决 普通最小二乘法 的一些问题。岭回归系数最小化的是带惩罚项的残差平方和,数学形式如下:
其中,α>= 0是一个控制缩减量(amount of shrinkage)的复杂度参数:α的值越大,缩减量就越大,故而线性模型的系数对共线性(collinearity)就越鲁棒。(L2正则化)换句话说,让各个特征对结果的影响尽可能的小,但也能拟合出不错的模型。
与普通最小二乘法一样,Ridge 会调用 fit 方法来拟合数组 X, y,并且将线性模型的系数 ω存储在其成员变量 coef_,截距存储在intercept_:
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=.5)
ridge.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
print("coef: {}".format(ridge.coef_))
print("intercept: {:.2f}".format(ridge.intercept_))
coef: [0.34545455 0.34545455]
intercept: 0.14
%config InlineBackend.figure_format=‘svg‘ # 矢量图设置
下面用代码实现一个岭回归的案例
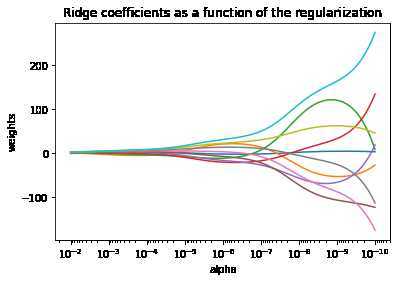
展示共线性(collinearity)对估计器系数的影响
这个例子中用到的模型是岭回归估计器(Ridge)。每种颜色表示系数向量的不同特征,并将其显示为正则化参数的函数。
此示例还显示了将岭回归应用于高度病态(ill-conditioned)矩阵的有效性。对于这样的矩阵,目标变量的微小变化会导致计算出的权重的巨大差异。在这种情况下,设置一定的正则化(alpha)来减少这种变化(噪声)是很有用的。
当alpha很大时,正则化效应将会主导(控制)平方损失函数,线性模型的系数也将趋于零。在路径的末尾,当alpha趋于零时,系数趋于没有设置正则化项的普通最小二乘法的系数,系数会出现很大的震荡(为高度病态矩阵)。
总共有10个系数,10条曲线,一一对应。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
# X 是一个10x10的 希尔伯特矩阵(Hilbert matrix)(高度病态且正定)
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
# 计算路径(Compute paths)
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
ridge = Ridge(alpha=a, fit_intercept=False) # 每个循环都要重新实例化一个estimator对象
ridge.fit(X, y)
coefs.append(ridge.coef_)
# 画图
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale(‘log‘)
ax.set_xlim(ax.get_xlim()[::-1]) # 反转数轴,越靠左边alpha越大,正则化越强
plt.xlabel(‘alpha‘)
plt.ylabel(‘weights‘)
plt.title(‘Ridge coefficients as a function of the regulariization‘)
plt.axis(‘tight‘)
RidgeCV 通过内置的 alpha 参数的交叉验证来实现岭回归。该对象与 GridSearchCV的使用方法相同,只是它默认为Generalized Cross-Validation(广义交叉验证GCV),这是一种有效的留以验证方法(LOO-CV):
from sklearn.linear_model import RidgeCV
ridge_cv = RidgeCV(alphas=[0.1, 1.0, 10.0], cv=3)
ridge_cv.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
print("coef: {}".format(ridge_cv.coef_))
print("alpha: {}".format(ridge_cv.alpha_))
coef: [0.44186047 0.44186047]
alpha: 0.1原文:https://www.cnblogs.com/wsilj/p/12844996.html