PNN点击率预估模型公式推导

1.

$l_{p}^{n}=\boldsymbol{W}_{p}^{n} \odot \boldsymbol{p}=\sum_{i=1}^{N} \sum_{j=1}^{N} \theta_{i}^{n} \theta_{j}^{n}\left\langle\boldsymbol{f}_{i}, \boldsymbol{f}_{j}\right\rangle=\left\langle\sum_{i=1}^{N} \boldsymbol{\delta}_{i}^{n}, \sum_{i=1}^{N} \boldsymbol{\delta}_{i}^{n}\right\rangle$

$\delta_{i}^{n}=\theta_{i}^{n}\boldsymbol{f}_{i}$

所以

$l_{p}^{n}=||\sum_{i=1}^{n}\delta_{i}^{n}||=||\sum_{i=1}^{n}\theta_{i}^{n}\boldsymbol{f}_{i}||$

有两个疑问：

1.WHY？$\sum_{i=1}^{N} \sum_{j=1}^{N} \theta_{i}^{n} \theta_{j}^{n}\left\langle\boldsymbol{f}_{i}, \boldsymbol{f}_{j}\right\rangle=\left\langle\sum_{i=1}^{N} \boldsymbol{\delta}_{i}^{n}, \sum_{i=1}^{N} \boldsymbol{\delta}_{i}^{n}\right\rangle$

2.文中说$\left\langle \sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}},\sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}} \right\rangle = \left\| \sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}} \right\|$

但是计算出来$\left\langle \sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}},\sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}} \right\rangle \ne \left\| \sum\limits_{i=1}^{N}{\mathbf{\delta }_{i}^{n}} \right\|$

PNN点击率预估模型公式推导

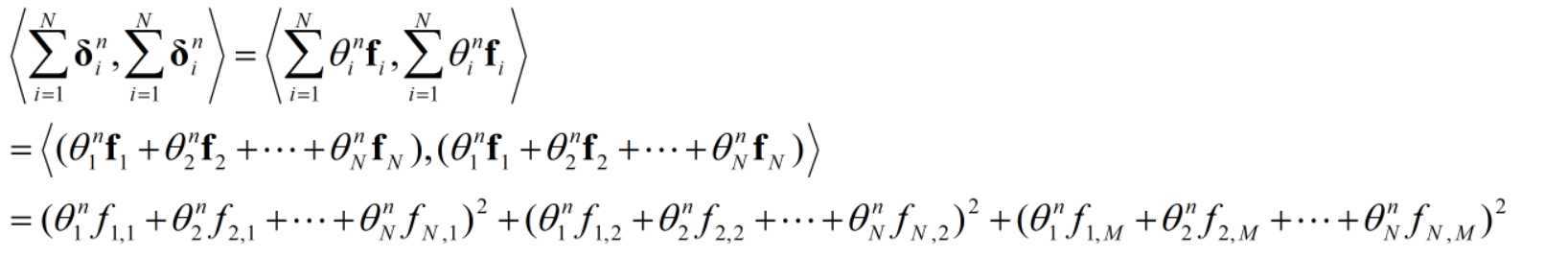
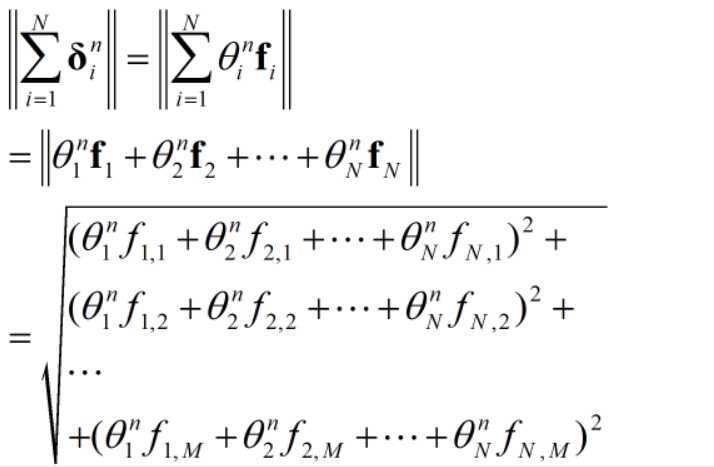
原文：https://www.cnblogs.com/sunupo/p/12847007.html