[TOC]

字典树

概述

树的形态：树根为空值，有26子节点（根据实际情况，可能具体问题不需要真实有。另外不同问题还可以扩展，比如加大小写兼有的需要双倍，但需要做好规定），而每一个子节点另外又包含26个子节点，根据需要递归下去。

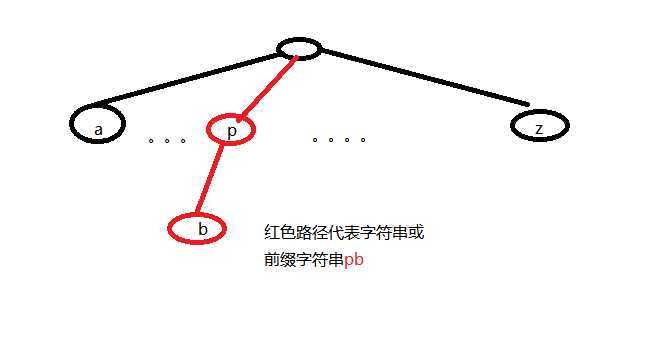
功能：从树根到某一结点的路径可以代表一个具体的字符串。

下面的图片展示了简单的结构。

常见的应用

• 字符串检索。
• 词频统计。
• 字符串排序。
• 前缀匹配

实例

?

题目：很多单词有10个以内的小写单词组成，问这些单词中以某个字符串为前缀的单词有多少个？

思路：简单字典树，前缀匹配问题。

本题可采用数组建树的方式，以节约空间。num数组保存节点信息（即个数），辅助的二维数组tire [ i ] [ j ]保存父节点i的第j个节点在数组中的位置。

插入操作，依次遍历字符串，并寻找到相应的节点在数组中位置使其加一，如果没有该节点则增加节点。

查询操作，遍历字符串，如果发现没有当前对应的结点，则返回0，如此判断到遍历结束，返回整个字符串对应结点的数量。

代码

 #include <iostream>
#include<string>
#include<cstdio>
#include<cstring>
using namespace std;
int pos = 0;
int tire[1010000][26];
int num[1010000];
void insert(char s[] ){
    int tmp = 0;
    for (int i = 0; s[i] ; i++){
        int x = s[i] - 97;
        if (tire[tmp][x] == 0) {
            tire[tmp][x] = ++pos;
        }
        tmp = tire[tmp][x];
        num[tmp]++;
    }
}
int find(char s[]) {
    int tmp = 0;
    for (int i = 0; s[i] ; i++) {
        int x = s[i] - 97;
        if (tire[tmp][x] == 0) return 0;
        tmp = tire[tmp][x];
    }
    return num[tmp];
}
int main()
{
    char s[11];

    while (gets(s) && s[0]) {
        insert(s);
    }
    while (gets(s)) {
        cout << find(s) << endl;
    }

}

数据结构_字符串

原文：https://www.cnblogs.com/508335848vf/p/12849017.html