CodeForces 526G Spiders Evil Plan

https://codeforces.com/contest/526/problem/G

\(n\) 个节点的树,每条边有边权, \(q\) 次询问, 强制在线, 每次询问给出 \((x,y)\) ,需要找到 \(y\) 条路径满足

• 至少一条路径包含 \(x\)
• 所有路径的并集形成一个联通块
• 并集的边权和尽量大

\(1 \le n,q \le 10^5\) , \(1 \le x,y \le n\)

Tutorial

我们要求的实际上是包含 \(x\) 的并集长度最长的 \(y\) 条路径. 设 \(S\) 为这些路径的并集(包含点和边).

首先,对于每个询问 \((x,y)\) ,一定存在一种 \(S\) 为联通块的最优方案,如图

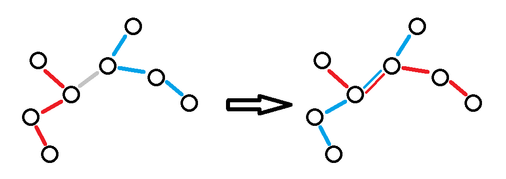
所以我们可以得到下面的定理

• 一个有 \(2k\) 个叶子的树,可以表示为 \(k\) 条路径的并集

证明:

首先随意两个叶子之间连边,如果存在一条边 \(u,v\) 不连通,我们可以将 \(u\) 子树中的路径 \((a,b)\) 和 \(v\) 子树中的路径 \((c,d)\) 变为 \((a,c)\) 和 \((b,d)\)

所以我们可以将 \(x\) 设为树的根,然后每次选择当前贡献最大的叶子,一共进行 \(2y\) 次,即可得到答案.

由于有多组询问,所以需要优化.

考虑对于树上的一条直径 \((a,b)\) ,一定有 \(a \in S\) 或 \(b \in S\)

所以就以 \(a\) 和 \(b\) 为根分别做一次上述操作.对于一个询问,在两颗树中分别查询,以以 \(a\) 为根的树为例:

如果 \(x \in S\) ,那么不需要其他操作.

否则删除某个叶子,使得加入 \(x\) 后答案最大.

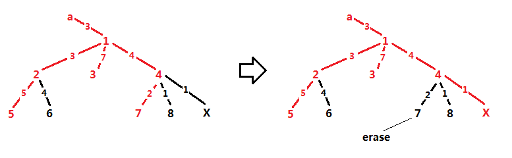
具体做法可以参考https://codeforces.com/contest/526/submission/79270659

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define lson u << 1, l, mid
#define rson u << 1 | 1, mid + 1, r
#define fi first
#define se second
template<class T> inline bool Cmax(T &x, T y) { return x < y ? x = y, 1 : 0; }
typedef pair<int, int> pii;
const int maxn = 1e5 + 50;
int n, q;
int a, b;
int k;
int A[maxn];
int dis[maxn];
int head[maxn];
struct edge
{
    int to, nex, cost;
    edge(int to = 0, int nex = 0, int cost = 0) : to(to), nex(nex), cost(cost) {}
};
vector<edge> G;
inline void addedge(int u, int v, int w)
{
    G.push_back(edge(v, head[u], w)), head[u] = G.size() - 1;
    G.push_back(edge(u, head[v], w)), head[v] = G.size() - 1;
}
namespace seg
{
    const int maxnode = maxn << 2;
    int tag[maxnode];
    pii mx[maxnode];
    inline void change(int u, int d)
    {
        mx[u].fi += d;
        tag[u] += d;
    }
    inline void pushdown(int u)
    {
        if (tag[u])
        {
            change(u << 1, tag[u]);
            change(u << 1 | 1, tag[u]);
            tag[u] = 0;
        }
    }
    inline void pushup(int u)
    {
        mx[u] = max(mx[u << 1], mx[u << 1 | 1]);
    }
    void build(int u, int l,int r)
    {
        tag[u] = 0;
        if (l == r)
        {
            mx[u] = make_pair(A[l], l);
            return;
        }
        int mid = (l + r) >> 1;
        build(lson);
        build(rson);
        pushup(u);
    }
    void update(int u, int l,int r,int ql,int qr,int qv)
    {
        if (l == ql && r == qr)
        {
            change(u, qv);
            return;
        }
        pushdown(u);
        int mid = (l + r) >> 1;
        if (qr <= mid) update(lson, ql, qr, qv);
        else if (ql > mid) update(rson, ql, qr, qv);
        else
        {
            update(lson, ql, mid, qv);
            update(rson, mid + 1, qr, qv);
        }
        pushup(u);
    }
}
struct Tree
{
    int dfc;
    int st[maxn], ed[maxn];
    int mx[maxn];
    int dis[maxn];
    int res[maxn];
    int rnk[maxn];
    int val[maxn];
    int vis[maxn];
    int parent[maxn][20];
    void dfs(int u)
    {
        st[u] = ++dfc, rnk[dfc] = u;
        mx[u] = dis[u];
        for (int i = 1; i < 20; ++i)
            parent[u][i] = parent[parent[u][i - 1]][i - 1];
        for (int i = head[u]; ~i; i = G[i].nex)
        {
            int v = G[i].to; 
            int w = G[i].cost;
            if (v == parent[u][0]) continue;
            dis[v] = dis[u] + w;
            val[v] = w;
            parent[v][0] = u;
            dfs(v);
            Cmax(mx[u], mx[v]);
        }
        ed[u] = dfc;
    }
    void init(int root)
    {
        dfs(root);
        for (int i = 1; i <= n; ++i)
            A[i] = dis[rnk[i]];
        seg :: build(1, 1, n);
        for (int y = 1; y <= n; ++y)
        {
            pii t = seg :: mx[1];
            res[y] = res[y - 1] + t.fi;
            debug("%d %d\n", y, res[y]);
            for (int u = rnk[t.se]; !vis[u]; u = parent[u][0])
            {
                vis[u] = y;
                seg :: update(1, 1, n, st[u], ed[u], -val[u]);
                if(u == root) break;
            }
        }
        // debug("---\n");
        // for (int i = 1; i <= n; ++i)
        //     debug("%d %d\n", i, vis[i]);
    }
    int jump(int u,int k)
    {
        for (int i = 19; ~i; --i)
            if(vis[parent[u][i]] > k)
                u = parent[u][i];
        return parent[u][0];
    }
    int sol(int x, int y)
    {
        if (vis[x] <= y)
            return res[y];
        int u = jump(x, y - 1);
        int an = res[y - 1] + mx[x] - dis[u];
        // debug("%d %d %d %d\n", x, y, u, an);
        u = jump(x, y);
        // debug("%d %d %d %d\n", x, y, u, res[y] - mx[u] + mx[x]);
        return max(an, res[y] - mx[u] + mx[x]);
    }
} Ta, Tb;
void dfs(int u, int fa)
{
    if(k == -1 || dis[u] > dis[k]) k = u;
    for (int i = head[u]; ~i; i = G[i].nex)
    {
        int v = G[i].to;
        int w = G[i].cost;
        if (v == fa) continue;
        dis[v] = dis[u] + w;
        dfs(v, u);
    }
}
void find_d()
{
    k = -1;
    dfs(1, -1);
    a = k;
    k = -1;
    dis[a] = 0;
    dfs(a, -1);
    b = k;
    // debug("%d %d\n", a, b);
}
void sol()
{
    find_d();
    Ta.init(a);
    Tb.init(b);
    int lastans = 0;
    for(int i = 1; i <= q; ++i)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        x = (x + lastans - 1) % n + 1;
        y = (y + lastans - 1) % n + 1;
        y = min(n, (y << 1) - 1);
        // debug("%d %d\n", x, y);
        printf("%d\n", lastans = max(Ta.sol(x, y), Tb.sol(x, y)));
    }
}
int main()
{
    scanf("%d%d", &n, &q);
    memset(head, -1, sizeof(head));
    for (int i = 1; i < n; ++i)
    {
        int u, v, l;
        scanf("%d%d%d", &u, &v, &l);
        addedge(u, v, l);
    }
    sol();
    return 0;
}

CodeForces 526G Spiders Evil Plan

原文：https://www.cnblogs.com/ljzalc1022/p/12853659.html