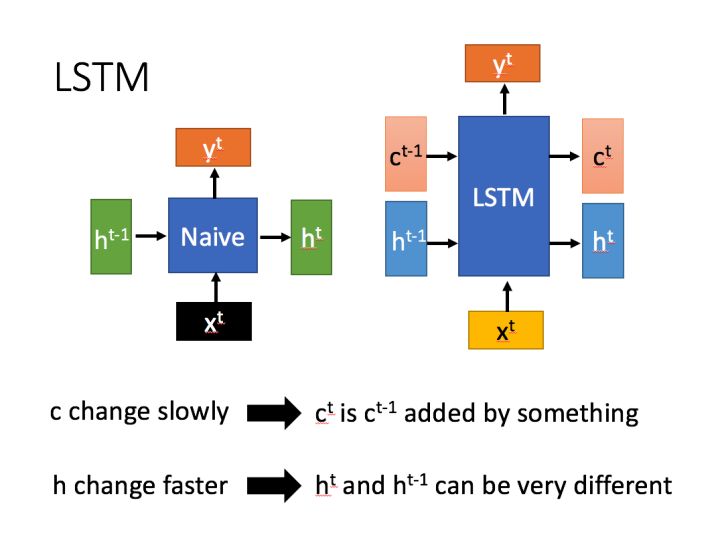
LSTM有两个传输状态,一个 \(c^t\)(cell state),和一个 \(h^t\)(hidden state)
\(c^t\)保存模型的长期记忆,在训练过程中改变的速度较慢, 而\(h^t\)在训练过程中变化的速度则比较快。
首先使用LSTM的当前输入\(x_t\)和上一个状态传递下来的\(h_{t-1}\)拼接计算得到四个中间变量:
\(z = tanh(W\cdot[h_{t-1},x_t] + b)\)
\(z^i = \sigma(W_i\cdot[h_{t-1},x_t] + b_i)\)
\(z^f = \sigma(W_f\cdot[h_{t-1},x_t] + b_f)\)
\(z^o = \sigma(W_o\cdot[h_{t-1},x_t] + b_o)\)
这里的\(i,f,o\)分别代表input gate, foget gate, output gate。运算符\([a,b]\)表示把a和b拼接成一个大的矩阵。
接下来:
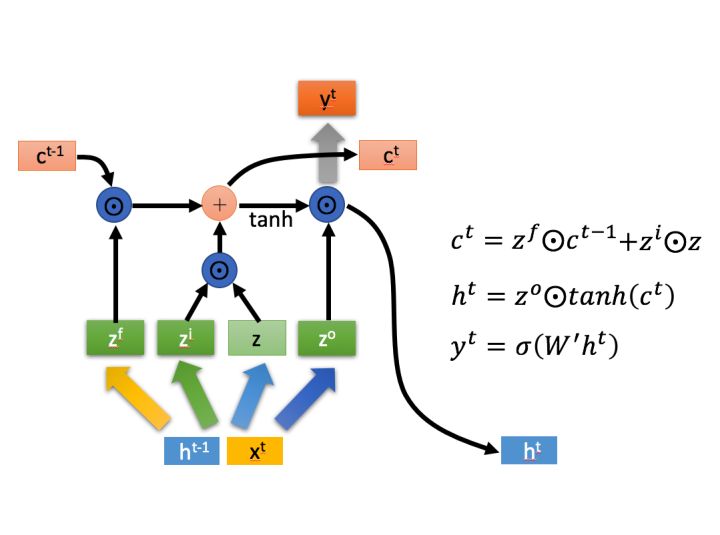
上图中 \(\bigodot\) 代表Hadamard Product,也就是操作矩阵中对应的元素相乘。 运算符 \(+\) 表示矩阵加法。
首先,\(z^f\)作为遗忘门控,筛选上一个\(c^{t-1}\)中哪些内容需要遗忘。
接着,\(z^i\)作为输入门控,对模型输入\(z\) 中的内容进行筛选,然后把筛选后的结果合并到\(c^t\)中。
最后,使用 \(tanh()\) 对\(c^t\)进行放缩,然后经输出门控\(z^o\)过滤,再通过一个全链接layer,得到模型输出。
在原本\([h_{t-1},x_t]\)拼接的基础上,再拼上cell state,即:
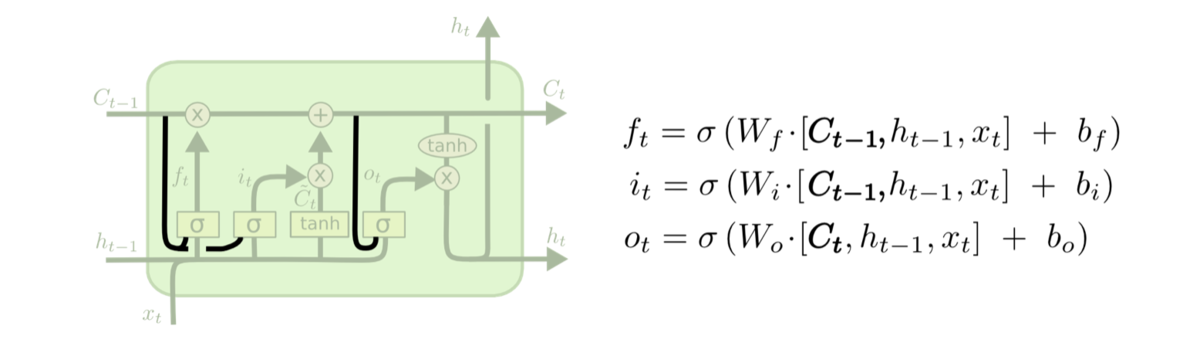
这样使得各个门结构可以看到cell state中的信息,在某些场景下提高了模型训练效果
由于LSTM的参数过多,所以其训练难度相对较大。因此,我们往往会使用效果和LSTM相当但参数更少的GRU来构建大训练量的模型。
论文:Bidirectional recurrent neural networks
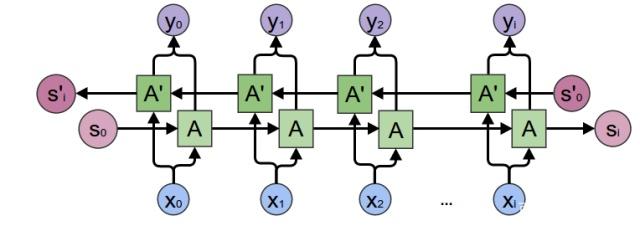
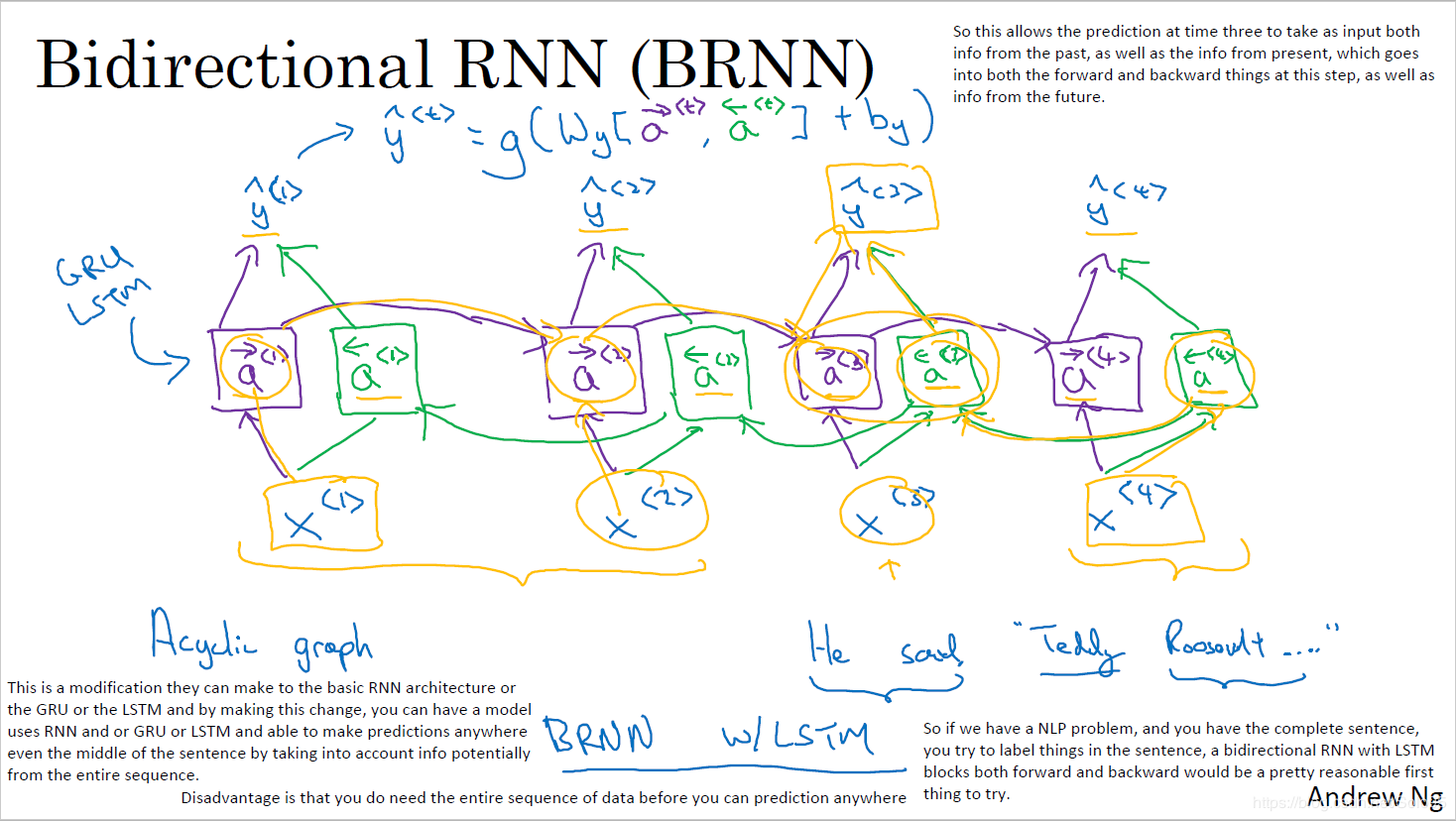
由于模型在理解句子时,常常需要完整的句子信息(既包含输入词前面的内容,也包含输入词后面的内容),因此双向RNN诞生了。
双向RNN有两种类型的连接,一种是向前的,这有助于我们从之前的表示中进行学习,另一种是向后的,这有助于我们从未来的表示中进行学习。
正向传播分三步完成:
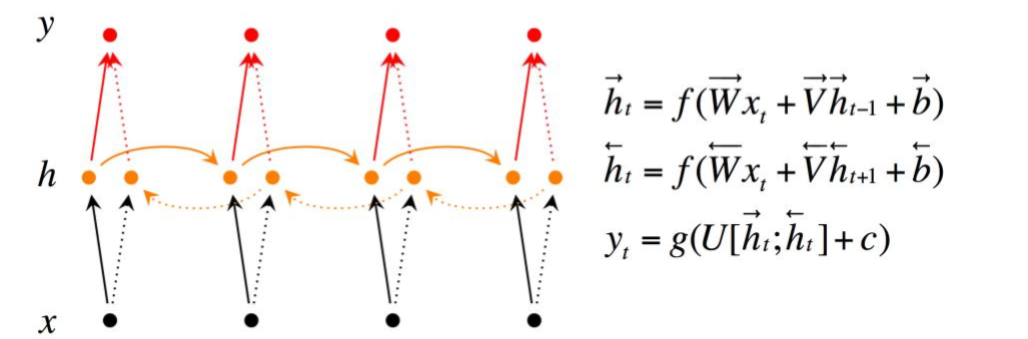
这里的分号代表把两个向量连接在一起
CS224n 从机器翻译到Attention 这个从45:28开始看
基于RNN的机器翻译模型存在一个问题,就是模型在翻译时依赖于输入序列最后传递的隐藏层参数(如下图中的\(h_4\)),如果前面输入的句子是个长句,则模型在翻译时很容易遗忘前面输入的句子。
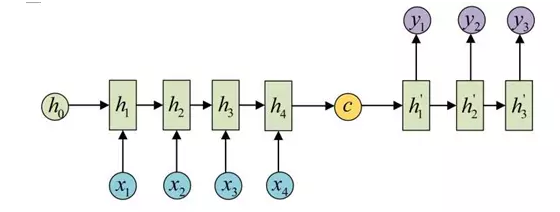
Attention机制让模型在翻译时可以读到输入序列的所有隐藏层状态(\(h_1,h_2,h_3,h_4\))并且自由地选择哪些是它需要关注的东西,因此在一定程度上解决了上述问题。
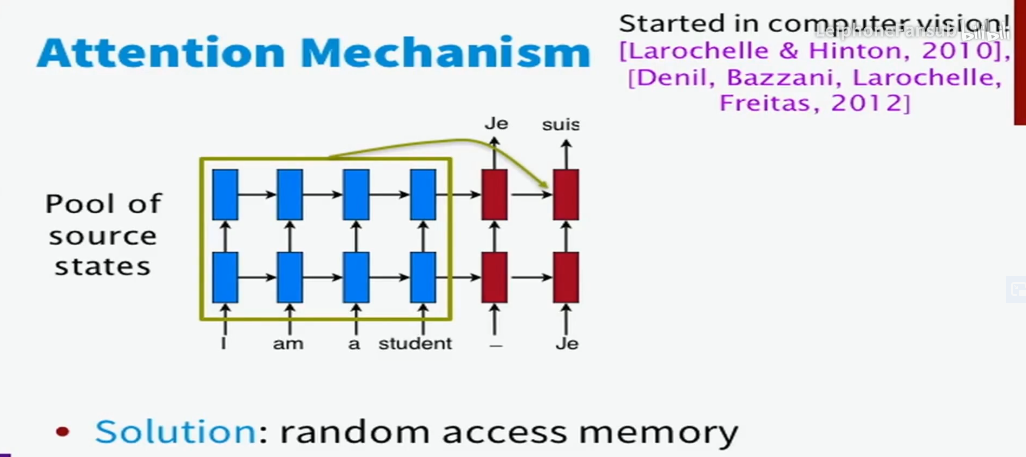
因此,我们可以说,attention机制使得翻译系统可以利用更多的上下文信息(数据也证明了这一点,因为带有attention的模型在长句的翻译上表现得更加出色)

self-attention机制可以理解为一个新的layer,它和RNN一样,输入一个sequence,输出一个sequence:
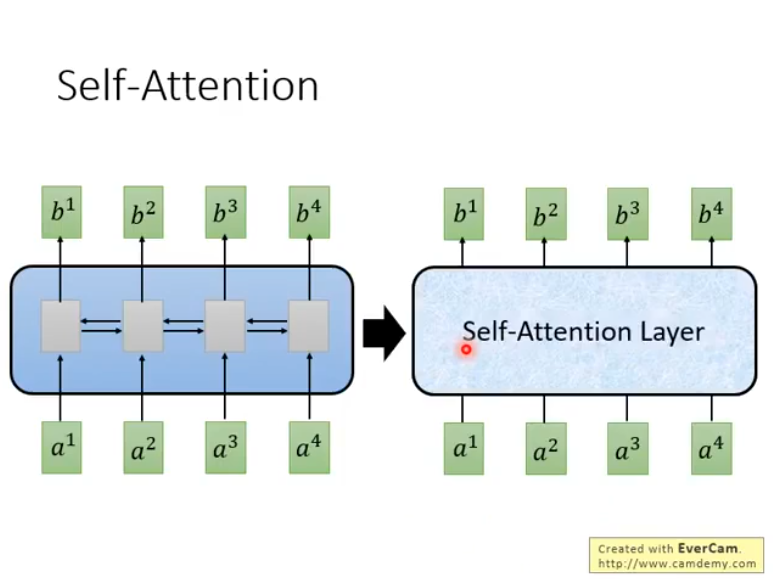
它出自谷歌2017年发布的paper:Attention Is All You Need
那么它具体是怎么工作的呢?
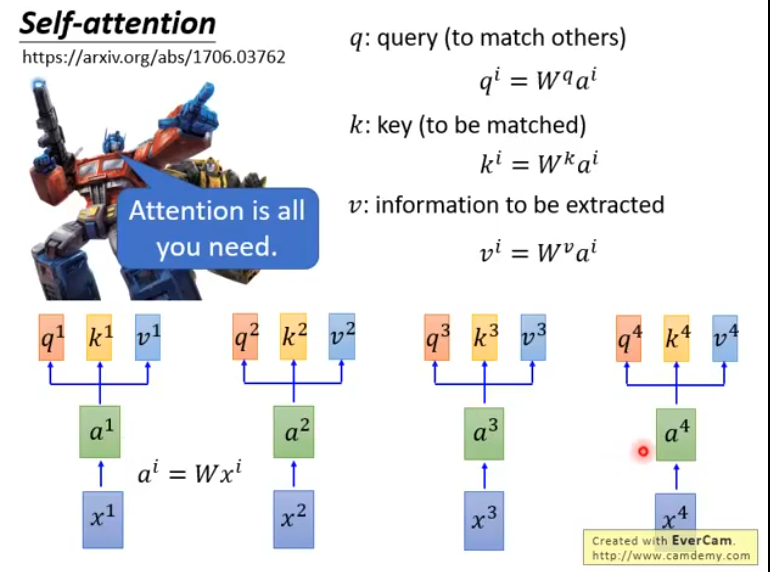
首先,\([x^1, x^2, ..., x^n]\)是一串输入序列,对于每一个\(x^i\),我们让它通过一个全链接层得到embedding:\(a^i\),也就是\(a^i = Wx^i\), 接下来,让\(a^i\)分别乘以三个不同的矩阵\(W^q\), \(W^k\), \(W^v\)得到\(q^i\), \(k^i\), \(v^i\)三个不同的向量,它们分别代表query, key和information to be extracted
接下来,拿每一个\(q\)对每一个\(v\)做attention,以\(q^1\)为例:
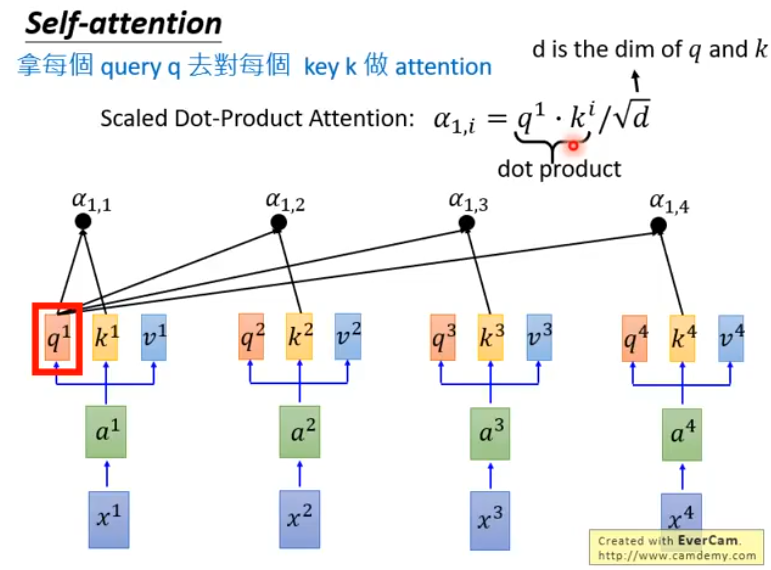
这里展示的\(a_{1,i}=q^1\cdot k^i/\sqrt{d}\)只是一种attention的做法(Scaled Dot-Product Attention),除此之外,还有很多种计算Attention的方法,包括:
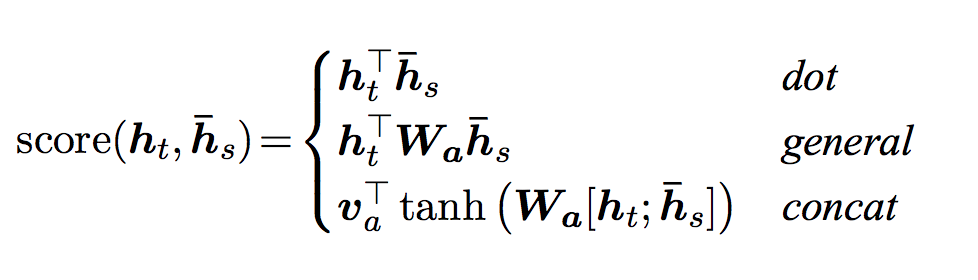
它们有一个共同的特征:都是吃两个向量,然后输出一个值,代表由这两个向量计算出的得分
接下来,让得到的\([a_{1,1},...,a_{1,n}]\)通过一个softmax layer,得到\([\hat{a}_{1,1},...,\hat{a}_{1,n}]\):
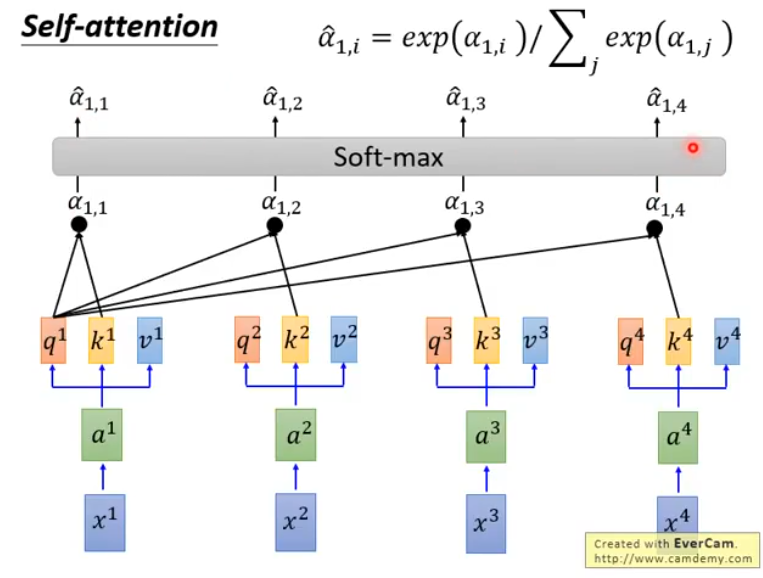
然后,我们把\(\hat{a}_{1,i}\)和每一个\(v^i\)相乘,并把结果累加起来,得到\(b^1 = \sum_i a_{1,i}v^i\):
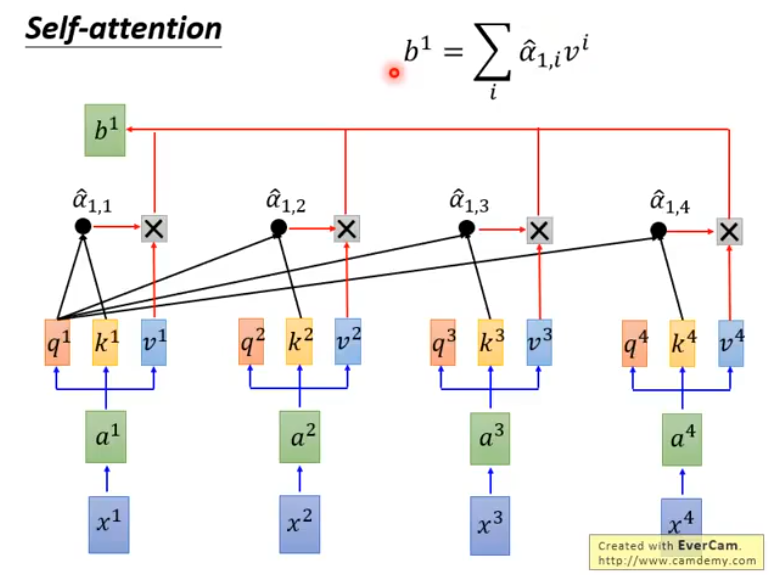
以此类推,得到的\([b^1, b^2,..,b^n]\)就是self-attention的输出序列了。与一般的RNN不同的是,模型输出的每一个\(b^i\)都考虑了从输入序列\([x^1, x^2,...,x^n]\)中获取的全部信息。
让我们用矩阵乘法总结一下整个过程:
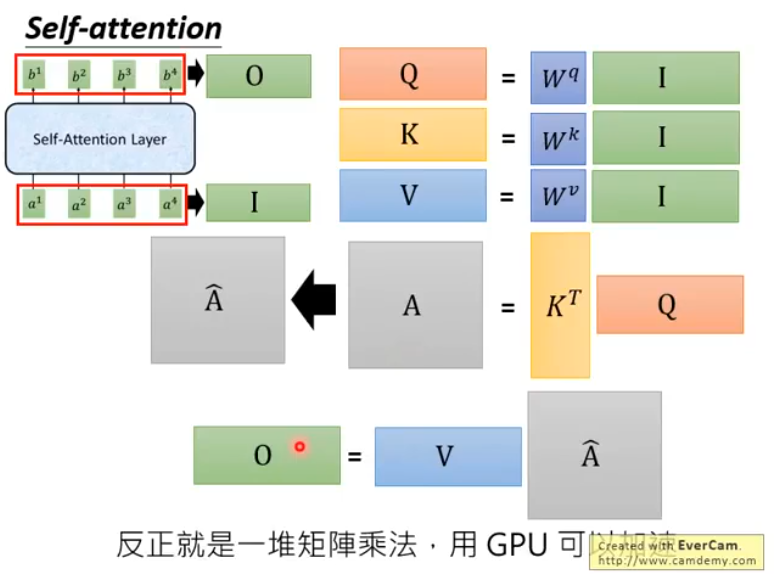
首先,输入序列通过一个全链接层转换成embedding I, 然后分别乘上三个不同的矩阵\(W^q,W^k,W^v\)得到矩阵\(Q, K, V\),接着对矩阵\(K\)和\(Q\)进行运算得到Attention,并对Attention中的每一列进行softmax得到\(\hat{A}\),最后,用\(V\)与\(\hat{A}\)相乘,得到输出序列\(O\)
attenion有一个变体叫Multi-head,它与原版本主要的差异就是针对每一个q,k,v,算法会让它们再乘上n个不同的矩阵得到\([q_1,q_2,...,q_n]\),\([k_1,k_2,...,k_n]\),\([v_1,v_2,...,v_n]\),它们分别进行attention运算,得到\([b_1,b_2,...,b_n]\),最后我们可以对\([b_1,b_2,...,b_n]\)进行降维(比如再加一个全链接层),得到输出序列\(B\):

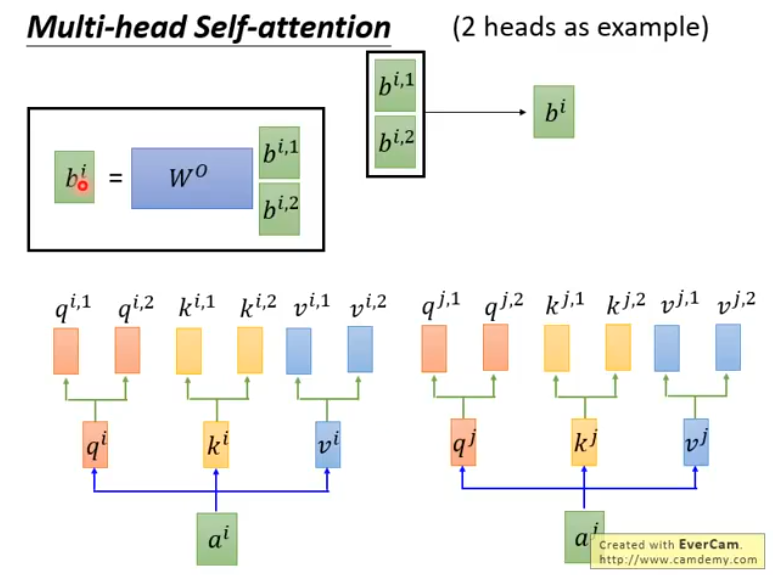
Multi-head的好处:
关于Transformer,这篇文章(https://www.cnblogs.com/ylHe/p/10193166.html)讲的非常好
Transformer就是引入attention机制的seq2seq模型:
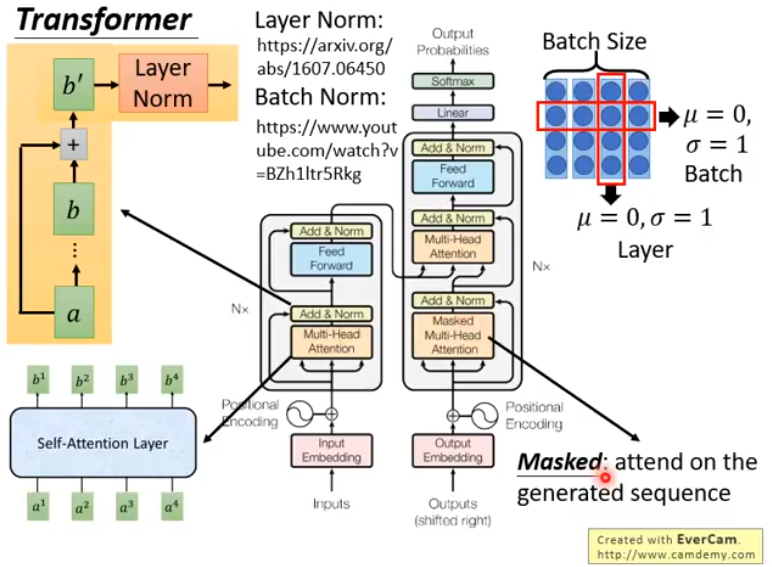
在Encoder中,我们先把输入序列转化成embedding,然后加上positional encoding(关于这个向量的具体意义,可参考李宏毅-Transformer[27:59-33:47]中的介绍)
接着,执行Multi-Head Attention,接着把Attention Layer的输入\(a\)和输出\(b\)相加,得到\({b}‘\),再对\({b}‘\)做一个Layey Norm,然后再通过Feed Forward然后再做Add&Norm,把这整个过程重复N次,最终得到Encoder的输出结果
在Decoder中,我们使用了Masked Multi-Head Attention,这里的解释是:
训练的时候我们知道全部真实label,但是预测时是不知道的。可以首先设置一个开始符s,然后把其他label的位置设为pad,然后对这个序列y做masked attention,因为其他位置设为了pad,所以attention只会用到第一个开始符s,然后用masked attention的第一个输出做为query和编码层的输出做普通attention,得到第一个预测的label y,然后把预测出的label加入到初始序列y中的相应位置,然后再做masked attention,这时第二个位置就不再是pad,那么attention层就会用到第二个位置的信息,依此循环,最后得到所有的预测label y。其实这样做也是为了模拟传统attention的解码层(当前位置只能用到前面位置的信息)。
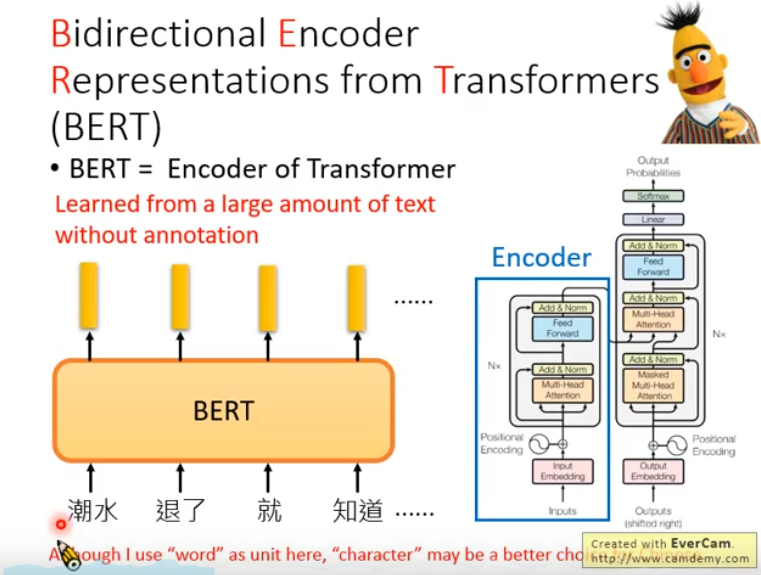
Bert的模型架构就是Transformers,它抽取的embedding就是Encoder的输出。
Bert通过两个任务进行训练:1. Masked LM,2. Next Sentence Prediction
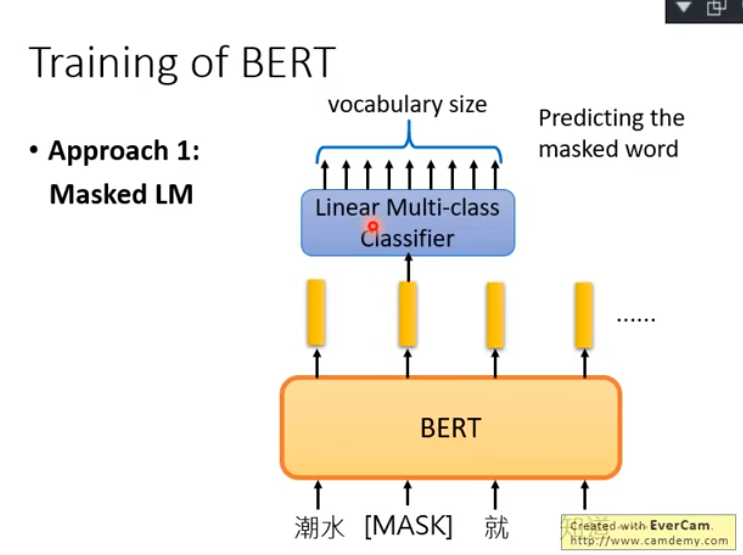
Masked LM是指:在句子中随机挑选15%的词汇,然后把Encoder对这些词得到的embedding输给一个线性分类器,判断这个分类器的预测准确率。这意味着,只有当bert抽取出的embedding足够好时,线性分类器才能有较高的分类准确率:
Next Sentence Prediction是指:预测两个句子是否是前后相邻的。在这个任务中需要引入两个特殊符号,一个是:[SEP],它代表两个句子的分界;另一个是[CLS],它代表之后的两个句子需要进行Next Sentence Prediction预测:
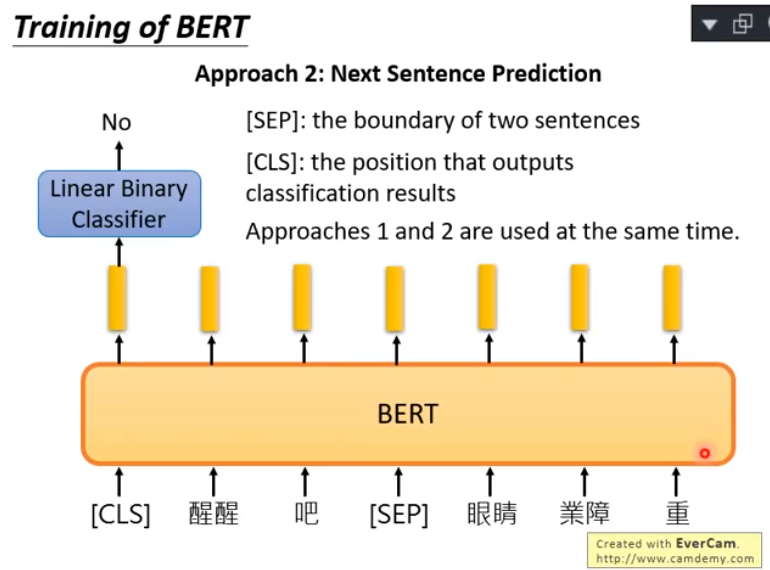
这两个任务将同时进行训练
参考:
LSTM / GRU / Attention / Transform / Bert
原文:https://www.cnblogs.com/lokvahkoor/p/12857937.html