[0001]合法序列

//想强迫自己每天写一篇题解哈哈哈

//解法中不加粗的部分是一些自己思维approach的过程

题目大意：

　　给定n,m，求有多少个长度为2*(n+m)的由A B构成的序列，可以拆成n个"AB"子序列和m个"BA"序列。eg. 序列ABAABB，可以将它拆成3个子序列AB（第1个和第6个字符）,BA（第2个和第3个字符）,AB（第4个和第5个字符）。对1e9+7取模。

　　多测。T<=1e5, 1<=n,m<=1e5。

题目解法：

　　首先我们需要知道一个序列合法需要满足的条件。

　　感性理解的话我们可以想到如果一个前缀有太多的A那么会导致后面有太多的B无法被用来组成“BA”。反之如果有太多的B则会导致"AB"的失配。

　　那么我们现在应该找到一个判断前缀合法的式子P 若一个序列的所有前缀均满足P 则合法。那么现在我们就要找到这个P。

　　考虑一个前缀，我们用cntA cntB分别代表该前缀中A和B的数量

　　1° cntA>cntB 此时BA可能失配

　　　该情况下我们最多可以组成的BA数量为cntB+(n+m)-cntA。因此若cntA-cntB>n，包含该前缀的序列一定不合法。

　　2° cntB>cntA 此时AB可能适配

　　　该情况下我们最多可以组成的AB数量为cntA+(n+m)-cntB。因此若cntA-cntB<-m，包含该前缀的序列一定不合法。

　　因此我们可以得到一个结论：

　　合法序列等价于对于任意一个前缀-m<=cntA-cntB<=n

　　接着我们可以想到dp状态及转移方程：f(cntA,cntB)=f(cntA-1,cntB)+f(cntA,cntB-1), (-m<=cntA-cntB<=n)

　　从数据范围猜测组合数乱搞。再结合这个转移方程的特征，将其转化为如下问题：

　　从(0,0)走到(n+m,n+m)，如下点不能走：

　　　　1. x-y>n

　　　　2. x-y<-m

　　显然这两种情况不重合，可以从总方案数中减去

　　考虑第一种情况，我们需要寻找经过特定右下角的路径条数（显然这个等腰直角三角形的边长为m）

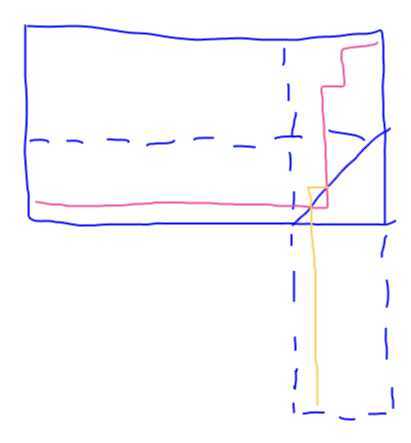
　　通过如上翻折转化我们将本来的问题转化为了从一个(2n+2+m)*m的方格左下角走到右上角的方案数。

　　显然这种关系是一一对应的。

　　第二种情况同理。

　　因此对于任意n,m，有答案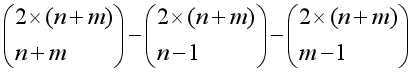

[0001]合法序列

原文：https://www.cnblogs.com/myrcella/p/12857986.html