1.理解分类与监督学习、聚类与无监督学习。
简述分类与聚类的联系与区别。
简述什么是监督学习与无监督学习。
2.朴素贝叶斯分类算法 实例
利用关于心脏病患者的临床历史数据集,建立朴素贝叶斯心脏病分类模型。
有六个分类变量(分类因子):性别,年龄、KILLP评分、饮酒、吸烟、住院天数
目标分类变量疾病:
–心梗
–不稳定性心绞痛
新的实例:–(性别=‘男’,年龄<70, KILLP=‘I‘,饮酒=‘是’,吸烟≈‘是”,住院天数<7)
最可能是哪个疾病?
上传手工演算过程。
|
|
性别 |
年龄 |
KILLP |
饮酒 |
吸烟 |
住院天数 |
疾病 |
|
1 |
男 |
>80 |
1 |
是 |
是 |
7-14 |
心梗 |
|
2 |
女 |
70-80 |
2 |
否 |
是 |
<7 |
心梗 |
|
3 |
女 |
70-81 |
1 |
否 |
否 |
<7 |
不稳定性心绞痛 |
|
4 |
女 |
<70 |
1 |
否 |
是 |
>14 |
心梗 |
|
5 |
男 |
70-80 |
2 |
是 |
是 |
7-14 |
心梗 |
|
6 |
女 |
>80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
7 |
男 |
70-80 |
1 |
否 |
否 |
7-14 |
心梗 |
|
8 |
女 |
70-80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
9 |
女 |
70-80 |
1 |
否 |
否 |
<7 |
心梗 |
|
10 |
男 |
<70 |
1 |
否 |
否 |
7-14 |
心梗 |
|
11 |
女 |
>80 |
3 |
否 |
是 |
<7 |
心梗 |
|
12 |
女 |
70-80 |
1 |
否 |
是 |
7-14 |
心梗 |
|
13 |
女 |
>80 |
3 |
否 |
是 |
7-14 |
不稳定性心绞痛 |
|
14 |
男 |
70-80 |
3 |
是 |
是 |
>14 |
不稳定性心绞痛 |
|
15 |
女 |
<70 |
3 |
否 |
否 |
<7 |
心梗 |
|
16 |
男 |
70-80 |
1 |
否 |
否 |
>14 |
心梗 |
|
17 |
男 |
<70 |
1 |
是 |
是 |
7-14 |
心梗 |
|
18 |
女 |
70-80 |
1 |
否 |
否 |
>14 |
心梗 |
|
19 |
男 |
70-80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
20 |
女 |
<70 |
3 |
否 |
否 |
<7 |
不稳定性心绞痛 |
3.使用朴素贝叶斯模型对iris数据集进行花分类。
尝试使用3种不同类型的朴素贝叶斯:
并使用sklearn.model_selection.cross_val_score(),对各模型进行交叉验证。
第一题
联系:
分类和聚类都是把每一条记录归应到对应的类别,对于想用分析的目标点,都会在数据集钟寻找离它最近的点,即二者都用到了NN算法。
区别:
分类是一种无监督学习,目的是确定点的类别,常用算法为KNN算法;
聚类是一种无监督学习,目的是将点的分类,常用算法是K-Means算法。
第二题
|
P(心梗)=16/20 |
P(不稳定性心绞痛)=4/20 |
|
P(性别=’男’|心梗)=7/16 |
P(性别=’男’|不稳定性心绞痛)=4/16 |
|
P(年龄<70|心梗)=4/16 |
P(年龄<70|不稳定性心绞痛)=4/16 |
|
P(KILLP=1|心梗)=9/16 |
P(KILLP=1|不稳定性心绞痛)=4/16 |
|
P(饮酒=’是’|心梗)=3/16 |
P(饮酒=’是’|不稳定性心绞痛)=4/16 |
|
P(吸烟=’是’|心梗)=7/16 |
P(吸烟=’是’|不稳定性心绞痛)=8/16 |
|
P(住院天数<7|心梗)=4/16 |
P(住院天数<7|不稳定性心绞痛)=8/16 |
P(心脏病)=(8/20)*(5/20)*(10/20)*(4/20)*(9/20)*(6/20)
比较P(心梗|心脏病)与P(不稳定性心绞痛|心脏病),即比较:
16*7*4*9*3*7*4与4*4*4*4*4*8*8,即比较:
3*7*7*9与2*4*4*8,易得左边大于右边,即:
该患者为心梗病的概率更高。
第三题
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB, MultinomialNB, BernoulliNB #高斯贝叶斯,多项式型高斯贝叶斯,伯努利型高斯贝叶斯
from sklearn.model_selection import cross_val_score #交叉验证分数
iris = load_iris()
data = iris[‘data‘]
target = iris[‘target‘]
# 高斯
Gnb_model = GaussianNB()
Gnb_model.fit(data, target)
Gnb_pre = Gnb_model.predict(data)
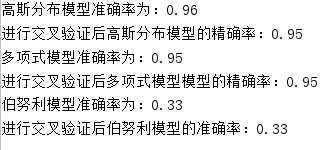
print("高斯分布模型准确率为:%.2F" % (sum(Gnb_pre == target) / len(data)))
print(‘进行交叉验证后高斯分布模型的精确率:%.2F‘ % cross_val_score(Gnb_model, data, target, cv=10).mean())
# 多项式
Mnb_model = MultinomialNB()
Mnb_model.fit(data, target)
Mnb_pre = Mnb_model.predict(data)
print("多项式模型准确率为:%.2F" % (sum(Mnb_pre == target) / len(data)))
print(‘进行交叉验证后多项式模型模型的精确率:%.2F‘ % cross_val_score(Mnb_model, data, target, cv=10).mean())
# 伯努利型
Bnb_model = BernoulliNB()
Bnb_model.fit(data, target)
Bnb_pre = Bnb_model.predict(data)
print("伯努利模型准确率为:%.2F" % (sum(Bnb_pre == target) / len(data)))
print(‘进行交叉验证后伯努利模型的准确率:%.2F‘ % cross_val_score(Bnb_model, data, target, cv=10).mean())
原文:https://www.cnblogs.com/seele233/p/12861111.html