剑指offer：数组中的逆序对

题意描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述

题目保证输入的数组中没有的相同的数字数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

解题思路

一、思路一

利用归并排序的思想

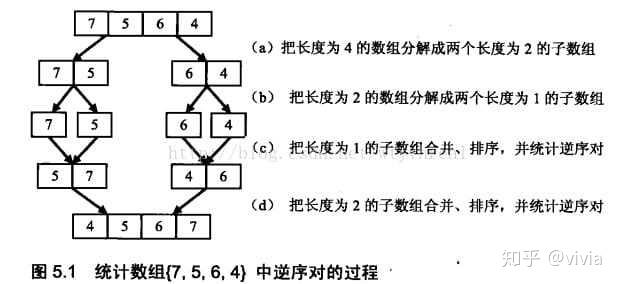
例如7,5,4,6可以划分为两段7,5和4,6两个子数组

1. 在7,5中求出逆序对，因为7大于5所以有1对
2. 在6,4中求出逆序对，因为6大于4所以逆序对再加1，为2
3. 对7,5和6,4进行排序，结果为5,7,和4,6
4. 设置两个指针分别指向两个子数组中的最大值，p1指向7，p2指向6
5. 比较p1和p2指向的值，如果大于p2，因为p2指向的是最大值，所以第二个子数组中有几个元素就有几对逆序对(当前有两个元素，逆序对加2,2+2=4)，7>6,比较完之后将p1指向的值放入辅助数组里，辅助数组里现在有一个数字7，然后将p1向前移动一位指向5
6. 再次判断p1和p2指向的值，p1小于p2，因为p1指向的是第一个子数组中最大值，所以子数组中没有能和当前p2指向的6构成逆序对的数，将p2指向的值放入辅助数组，并向前移动一位指向4，此时辅助数组内为6,7
7. 继续判断p1(指向5)和p2(指向4)，5>4,第二个子数组中只有一个数字，逆序对加1，4+1=5，为5对，然后将5放入辅助数组，第一个子数组遍历完毕，只剩下第二个子数组，当前只有一个4，将4也放入辅助数组，函数结束。辅助数组此时为4,5,6,7.逆序对为5.

public int InversePairs(int [] array) {
        int len = array.length;
        if(array== null || len <= 0){
            return 0;
        }
        return merge(array, 0, len-1);
    }
    private int merge(int[] array,int start,int end){
        if(start == end) return 0;
        int mid = (start + end) >> 1;	//中间值
        int left = merge(array,start,mid);
        int right = merge(array,mid+1,end);
        int i = mid,j = end;   //i指向左边最大的值，j指向右边最大的值
        int[] copy = new int[end-start+1];  //辅助数组
        int index = end - start; //辅助数组长度
        int count = 0;	//逆序对数
        while((i>=start) && (j>mid)){
            //分解为一个长度为1的子数组
            //进行合并
            if(array[i] > array[j]){  //左边最大的值 》 右边最大的值
                copy[index--] = array[i--]; //从大到小将i添加到copy，移动i指针
                count += j-mid; //对于i而言，有（j-mid）个值《 i
                if(count >1000000007){  //数值过大，取余
                    count %= 1000000007;
                }
            }else { //左边最大的值 《 右边最大的值
                copy[index--] = array[j--]; //将j添加大copy，移动指针
            }
        }
        while(i >= start){  //左边剩余的添加入辅助数组
            copy[index--] = array[i--];
        }
        while(j > mid){ //右边剩余的添加入辅助数组
            copy[index--] = array[j--];
        }
        i=0;
        while(start <= end){
            array[start++] = copy[i++]; //排序完成，放回原数组
        }
        return (left+right+count)%1000000007;
    }

剑指offer：数组中的逆序对

原文：https://www.cnblogs.com/le-le/p/12865714.html