用三角变换给出,
解析:函数\(f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1\)
\(=2sin(2x+\cfrac{\pi}{3})+1\)
若\(x\in [-\cfrac{\pi}{3},\cfrac{\pi}{4}]\),则可得
\(-\cfrac{2\pi}{3}\leq 2x\leq \cfrac{\pi}{2}\),则\(-\cfrac{\pi}{3}\leq 2x+\cfrac{\pi}{3}\leq \cfrac{5\pi}{6}\),
故当\(2x+\cfrac{\pi}{3}=-\cfrac{\pi}{3}\),即\(x=-\cfrac{\pi}{3}\)时,\(f(x)_{min}=f(-\cfrac{\pi}{3})=2\times (-\cfrac{\sqrt{3}}{2})+1=-\sqrt{3}+1\);
故当\(2x+\cfrac{\pi}{3}=\cfrac{\pi}{2}\),即\(x=\cfrac{\pi}{12}\)时,\(f(x)_{max}=f(\cfrac{\pi}{12})=2\times 1+1=3\);
用实际问题给出
分析:由\(\cfrac{b}{a}=\cfrac{sinB}{sinA}=\cfrac{1-cosB}{cosA}\),
得到\(sinBcosA+cosBsinA=sinA\),即\(sin(A+B)=sinA\)
则\(sinC=sinA\),即\(A=C\),
故\(a=b=c\),为等边三角形。
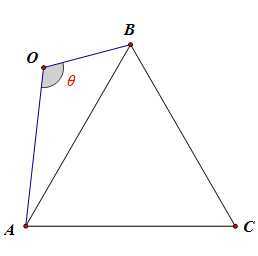
在\(\Delta AOB\)中,\(AB^2=2^2+1^2-2\cdot 2\cdot 1\cdot cos\theta=5-4cos\theta\),
故\(S_{OACB}=S_{\Delta AOB}+S_{\Delta ABC}\)
\(=\cfrac{1}{2}\cdot 2\cdot 1\cdot sin\theta+\cfrac{\sqrt{3}}{4}\cdot AB^2\)
\(=sin\theta+\cfrac{\sqrt{3}}{4}(5-4cos\theta)=2sin(\theta-\cfrac{\pi}{3})+\cfrac{5\sqrt{3}}{4}\)
当\(\theta-\cfrac{\pi}{3}=\cfrac{\pi}{2}\)时,即\(\theta=\cfrac{5\pi}{6}\in (0,\pi)\)时,四边形的面积有最大值,
且\(S_{max}=2+\cfrac{5\sqrt{3}}{4}=\cfrac{8+5\sqrt{3}}{4}\),故选\(B\)。
用向量运算给出,如向量的内积或平行或垂直关系给出;
\(f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1\)
\(f(x)=sin2x+\sqrt{3}(2cos^2x-1)+1\)
\(=sin2x+\sqrt{3}cos2x+1\)
\(=2sin(2x+\cfrac{\pi}{3})+1\)
用图像变换给出
(1)写出直线\(l\)的普通方程与曲线\(C\)的直角坐标方程;
(2)设曲线\(C\)经过伸缩变换\(\begin{cases}x‘=x\\y‘=\cfrac{1}{2}y\end{cases}\)得到曲线\(C‘\),设\(M(x,y)\)为曲线\(C‘\)上任意一点,求\(x^2-\sqrt{3}xy+2y^2\)的最小值,并求相应的点\(M\)的坐标。
分析:(1)消去参数\(t\),得到直线\(l\)的普通方程为\(\sqrt{3}x-y-\sqrt{3}+2=0\)
由\(\rho=2\),得到曲线\(C\)的直角坐标方程为\(x^2+y^2=4\);
(2)曲线\(C:x^2+y^2=4\)经过伸缩变换\(\begin{cases}x‘=x\\y‘=\cfrac{1}{2}y\end{cases}\)得到曲线\(C‘\),
即将\(x=x‘,y=2y‘\)代入\(C:x^2+y^2=4\)得到,\(x‘^2+4y‘^2=4\),
整理得到曲线\(C‘:\cfrac{x^2}{4}+y^2=1\)。
由曲线\(C‘\)的参数方程得到点\(M(2cos\theta,sin\theta)\),
即\(x=2cos\theta,y=sin\theta\),代入得到
\(x^2-\sqrt{3}xy+2y^2=(2cos\theta)^2-\sqrt{3}\cdot 2cos\theta\cdot sin\theta+2sin^2\theta\)
\(=4cos^2\theta+2sin^2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=2+2cos^2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=2+1+cos2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=3-2sin(2\theta-\cfrac{\pi}{6})\)
当\(2\theta-\cfrac{\pi}{6}=2k\pi+\cfrac{\pi}{2}(k\in Z)\),
即\(\theta=k\pi+\cfrac{\pi}{3}(k\in Z)\)时,
即点\(M(1,\cfrac{\sqrt{3}}{2})\)或\(M(-1,-\cfrac{\sqrt{3}}{2})\)时,
\(x^2-\sqrt{3}xy+2y^2\)的最小值为1.
用表格给出
用图像给出
分析:由图像可知,函数的最大值\(M=4\),最小值\(m=0\),故\(A=\cfrac{4-0}{2}=2\),\(b=\cfrac{4+0}{2}=2\),
又由于\(\cfrac{T}{4}=\cfrac{5\pi}{12}-\cfrac{\pi}{6}=\cfrac{\pi}{4}\),故\(T=\pi\),故\(\omega=\cfrac{2\pi}{\pi}=2\),
又\(2\times \cfrac{\pi}{6}+\phi=\cfrac{\pi}{2}\),解得\(\phi=\cfrac{\pi}{6}\in (-\cfrac{\pi}{2},\cfrac{\pi}{2})\),
故所求解析式为\(f(x)=2sin(2x+\cfrac{\pi}{6})+2\),故选\(D\)。
分析:由于函数\(y=sin(ωx+φ)\)的最小正周期为\(π\),故\(\omega=2\),又图象关于点\((-\cfrac{3\pi}{8},0)\)对称,
则\(2\times (-\cfrac{3\pi}{8})+\phi=k\pi\),故\(\phi=k\pi+\cfrac{3\pi}{4}\),\(k\in Z\) ,
当\(k=0\)时,\(\phi=\cfrac{3\pi}{4}\in (0,\pi)\),故解析式为\(y=sin(2x+\cfrac{3\pi}{4})\).
分析:这类题目一般需要先将\(f(x)\)转化为正弦型或者余弦型,
再利用给定的条件分别求\(\omega\)和\(\phi\),由\(f(x)=2Acos^2(\omega x+\phi)=A[cos2(\omega x+\phi)+1]-A=Acos(2\omega x+2\phi)\),
故其周期为\(T=\cfrac{2\pi}{2\omega}=\cfrac{\pi}{\omega}\),
又由题目可知\(\cfrac{T}{4}=\cfrac{\pi}{3}-\cfrac{\pi}{12}=\cfrac{\pi}{4}\),则\(T=\pi=\cfrac{\pi}{\omega}\),
故\(\omega=1\),则函数简化为\(f(x)=Acos(2x+2\phi)\),再利用直线\(x=\cfrac{\pi}{3}\)是函数\(f(x)\)图象上的一条对称轴,
故\(2\times \cfrac{\pi}{3}+2\phi=k\pi,(k\in Z)\),解得\(\phi=\cfrac{k\pi}{2}-\cfrac{\pi}{3}\),
令\(k=1\),则\(\phi=\cfrac{\pi}{6}\in (0,\cfrac{\pi}{2})\),满足题意,故\(f(x)=Acos(2x+2\phi)=Acos(2x+\cfrac{\pi}{3})\).
令\(2k\pi-\pi\leq 2x+\cfrac{\pi}{3}\leq 2k\pi(k\in Z)\),解得\(k\pi-\cfrac{2\pi}{3}\leq x \leq k\pi-\cfrac{\pi}{6}\),即单调递增区间为\(A.[k\pi-\cfrac{2\pi}{3} ,k\pi-\cfrac{\pi}{6}](k\in Z)\);
原文:https://www.cnblogs.com/wanghai0666/p/12868448.html