逻辑回归也属于有监督机器学习，逻辑回归就是用回归的办法来做分类的
输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题。
判别函数我们用线性的y = ,逻辑回归的函数呢,我们目前就用sigmod函数,函数如下:
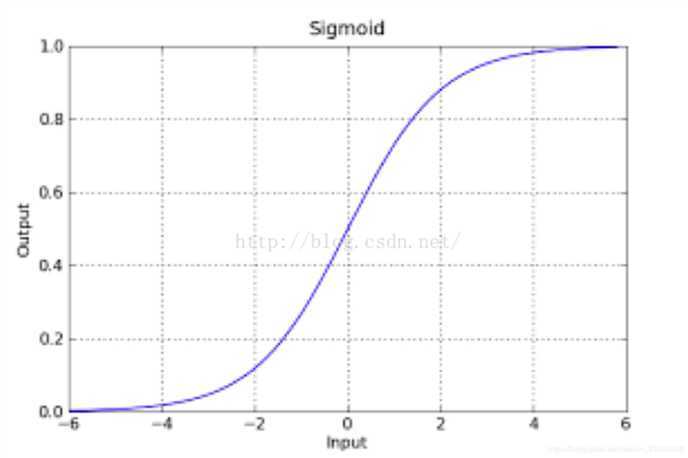
该函数具有很强的鲁棒性(鲁棒是Robust的音译，也就是健壮和强壮的意思),并且将函数的输入范围(∞,-∞)映射到了输出的(0,1)之间且具有概率意义.
g(z) = . 同时,因为g(z)函数的特性,它输出的结果也不再是预测结果,而是一个值预测为正例的概率,预测为负例的概率就是1-g(z).
函数形式表达:
P(y=0|w,x) = 1 – g(z)
P(y=1|w,x) = g(z)
P(正确) =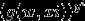
* 
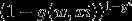yi为某一条样本的预测值,取值范围为0或者1.
如何找到一组可以让全都预测正确的概率最大的W.
逻辑回归(logistics regression)的损失函数,我们叫它交叉熵损失函数.
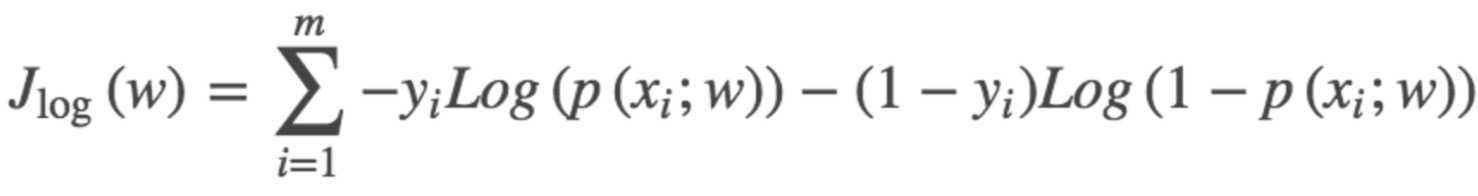
总结：使用逻辑回归分类的两个问题：1.如何降低离群值（异常值）的影响；
2.在正负例数据比例相差悬殊时预测效果不好：
使用最大似然估计来推导损失函数,那无疑,我们得到的结果就是所有样本被预测正确的最大概率.注意重点是我们得到的结果是预测正确率最大的结果,100个样本预测正确90个和预测正确91个的两组w,我们会选正确91个的这一组.那么,当我们的业务场景是来预测垃圾邮件,预测黄色图片时,我们数据中99%的都是负例(不是垃圾邮件不是黄色图片),如果有两组w,第一组为所有的负例都预测正确,而正利预测错误,正确率为99%,第二组是正利预测正确了,但是负例只预测出了97个,正确率为98%.此时我们算法会认为第一组w是比较好的.但实际我们业务需要的是第二组,因为正例检测结果才是业务的根本.
此时我们需要对数据进行欠采样/重采样来让正负例保持一个差不多的平衡,或者使用树型算法来做分类.一般树型分类的算法对数据倾斜并不是很敏感,但我们在使用的时候还是要对数据进行欠采样/重采样来观察结果是不是有变好.
逻辑回归和线性回归
如果乘法式子（最优化的目标函数和约束条件）中，自变量x被两个以上的参数影响，那么此模型是非线性的！
逻辑回归比线性回归要好。
两者都属于广义线性模型。
线性回归优化目标函数用的最小二乘法，而逻辑回归用的是最大似然估计。
逻辑回归只是在线性回归的基础上，将加权和通过sigmoid函数，映射到0-1范围内空间。
线性回归在整个实数范围内进行预测，敏感度一致，而分类范围，需要在[0,1]。而逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型。逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为(0,1)。逻辑回归的鲁棒性比线性回归要好。
原文链接：https://blog.csdn.net/weixin_39445556/java/article/details/83930186
原文：https://www.cnblogs.com/A-lam/p/12871163.html