滑动窗口
题面:
https://www.luogu.com.cn/problem/P1886
简单的单调队列题目,具体做法就不讲了
滑动窗口第K大
一说到第k大,很多dalao就会想到主席树
主席树确实可以,不过如果不想打主席树,可以用双堆实现滑动窗口第K大,既然是堆,那么就不用自己写,可以直接套用STL里的priority_queue (STL大法好!!)
建立一个大根堆,一个小根堆,共同维护区间信息
设窗口长度为m
m个元素当中最大的k个在小根堆里,其余的m-k个在大根堆
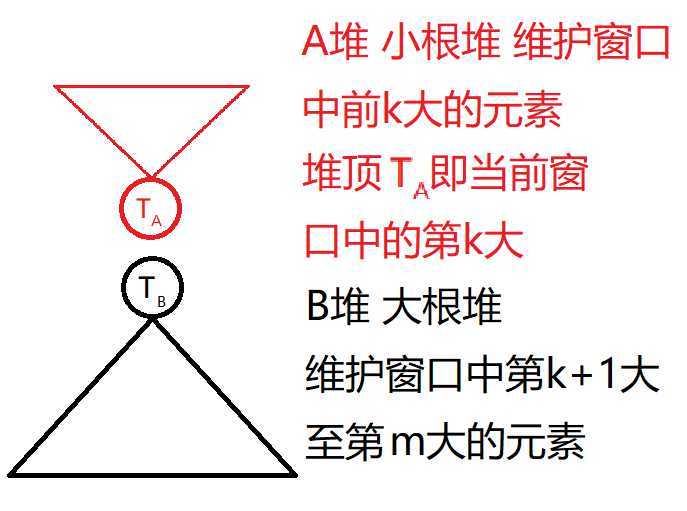
插入新元素或 删除旧元素时维护这一性质,具体如下:
每次窗口滑动,先删除滑出窗口的元素,然后比较新滑入窗口的数v与TA
如果v>=TA则将v放入A堆,否则放入B堆
接下来检查A堆的大小
如果A堆的大小=k+1,则将A堆的堆顶转移至B堆
如果A堆的大小=k-1,则将B堆的堆顶转移到A堆
这时TA即当前窗口的第k大
但是还有一个问题,如果使用STL的堆,那么就无法删除指定元素,也就是说在窗口滑动的时候,无法从堆中删除滑出窗口的元素
难道我们必须手动实现堆了吗?
当然不用,记不记得线段树的lazy标记?当某操作当前不方便完成,但暂时不影响运行结果时,可以打一个标记,当必须进行操作时,再进行操作
因为整个序列长度有限,那么我们就可以开一个数组记录每个元素是否在堆里,当需要删除滑出窗口的元素时,就在这个数组中把这个元素标记为不在堆内(但实际上堆里依然有这个元素)
就类似于一个人失踪超过一段时间就可以在法律上宣告这个人已经死亡
但和宣告死亡不同的是,当在堆顶发现已经“宣告死亡”的元素时,就把它pop掉,然后装作啥也没看见
就相当于发现一个已经宣告死亡的人,告诉他“你现在已经死了”然后当场枪毙
这样一来,就避免了手打任何数据结构
貌似这个算法加上莫队就可以实现离线查询区间第k大?具体实现有待探索
下面是我的代码
#include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #include <queue> const int N=100005; int n,l,k; int v[N]; struct nodeG { int val,pos; nodeG() {} nodeG(int x,int y) { val=x;pos=y; } bool operator <(const nodeG& x) const { return val<x.val; } }; struct nodeS { int val,pos; nodeS() {} nodeS(int x,int y) { val=x;pos=y; } bool operator <(const nodeS& x) const { return val>x.val; } }; template<typename node> class Heap { private: std::priority_queue<node> q; int size; bool in[N]; public: Heap() { memset(in,0,sizeof(in)); size=0; } void Push(int val,int pos) { if (!in[pos]) { q.push(node(val,pos)); in[pos]=true; size++; } } node Top() { node res; while (in[(res=q.top()).pos]==false) q.pop(); return res; } node Pop() { node res; while (in[(res=q.top()).pos]==false) q.pop(); q.pop(); size--; in[res.pos]=false; return res; } void Del(int x) { if (in[x]) size--; in[x]=false; } int Size() { return size; } bool Exist(int x) { return in[x]; } }; Heap<nodeS> rh; Heap<nodeG> bh; int main() { scanf("%d%d%d",&n,&l,&k); for (int i=1;i<=n;i++) scanf("%d",&v[i]); for (int i=1;i<=l;i++) { rh.Push(v[i],i); if (rh.Size()>k) { nodeS pp=rh.Pop(); bh.Push(pp.val,pp.pos); } } printf("%d ",rh.Top().val); for (int i=l+1;i<=n;i++) { int pout=i-l; if (rh.Exist(pout)) { rh.Del(pout); if (bh.Size()==0 || v[i]>bh.Top().val) rh.Push(v[i],i); else { bh.Push(v[i],i); nodeG pp=bh.Pop(); rh.Push(pp.val,pp.pos); } } else { bh.Del(pout); if (v[i]<rh.Top().val) bh.Push(v[i],i); else { rh.Push(v[i],i); nodeS pp=rh.Pop(); bh.Push(pp.val,pp.pos); } } printf("%d ",rh.Top().val); } return 0; }
原文:https://www.cnblogs.com/LMXZ/p/12234741.html