public class Traversing {

    public void print1(int n) {

        System.out.println("按斜对角线从中间向右上打印矩阵");
        for (int j = n; j > 0; j--) {
            for (int i = 0; i < j; i++) {
                System.out.print("(" + i + "," + (n - j + i) + ") ");
            }
            System.out.println();
        }
    }

    public void print2(int n){
        System.out.println("按列递增的自底向上打印");
        for (int j = 0; j < n; j++) {
            for (int i = j; i > -1; i--) {
                System.out.print("(" + i + "," + j + ") ");
            }
            System.out.println();
        }
    }

    public void print3(int n){
        System.out.println("按行递减从左到右打印");
        for (int i = n-1; i >= 0; i--) {
            for (int j = i; j < n; j++) {
                System.out.print("(" + i + "," + j + ") ");

            }
            System.out.println();
        }
    }

    public static void main(String[] args) {

        Traversing traversing = new Traversing();
        System.out.println("都可以处理dp[i][j]由{dp[i+1][j-1](左下),dp[i][j-1](左),dp[i+1][j](下)}三个方向决定");
        traversing.print1(5);
        traversing.print2(5);
        traversing.print3(5);

    }

}

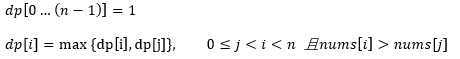
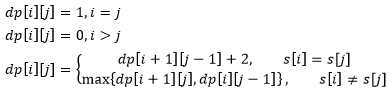
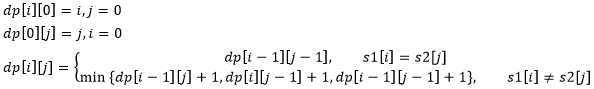
int minDistance(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    int[][] dp = new int[m + 1][n + 1];
    // base case
    for (int i = 1; i <= m; i++)
        dp[i][0] = i;
    for (int j = 1; j <= n; j++)
        dp[0][j] = j;
    // ?底向上求解
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            if (s1.charAt(i-1) == s2.charAt(j-1))
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] = min(
                        dp[i - 1][j] + 1,
                        dp[i][j - 1] + 1,
                        dp[i-1][j-1] + 1
                );
    // 储存着整个 s1 和 s2 的最?编辑距离
    return dp[m][n];
} 
int min(int a, int b, int c) {
    return Math.min(a, Math.min(b, c));
}