前言
没有想到前缀和也被单独拿出来作为一节来讲,不过也好,还可以顺便讲讲前面又碰到了一次的多维前缀和以及差分。
子目录列表
2.7 前缀和与差分
1、前缀和
前缀和:对于数列 a,其第 1, 2, ..., i 项之和,即 a[1] + a[2] + ... + a[i],称为数列 a 第 i 项的前缀和。
学过高中数学的数列章节就知道,“前缀和”和“前 n 项和 Sn”的概念是等价的。
前缀和有啥用?最简单的,如果我们要求数列某一个区间 [l, r] 之和,如果预处理了前缀和 sum,则直接 sum[r] - sum[l - 1] 就得到了区间和。

2、差分
和前缀和相对的一个概念。
差分:对于数列 a,其第 i 个元素和第 i - 1 个元素的差称为数列 a 第 i 项的差分。
令差分数组为 b,则存在:b[i] = a[i] - a[i - 1]
有意思的是,对差分数组求前缀和就又可以得到原数列 a 了。
sumb[i] = b[1] + b[2] + ... b[i] = a[1] + a[2] - a[1] + ... + a[i] - a[i - 1] = a[i]
那么我们拿着这个差分数组有什么用捏?
【例题】给定一个数列 a,进行 m 次操作,每次给定三个值 l, r, p,操作类型如下:
① 1 l r p,表示对 a[l..r] 的每一个元素加上 p;
② 2 l r,表示查询 a[l..r] 的元素和。
确保所有操作 ① 执行完后才会有操作 ②。
最简单的做法就是对于修改操作逐一加上 p,对于查询操作可以用前面的前缀和来求。但注意到题目最后这个限定:所有修改操作会在任意查询操作之前执行,这样其实我们可以拿差分数组做文章,每次只修改差分数组的两个端点即可,见下面的图解举例:
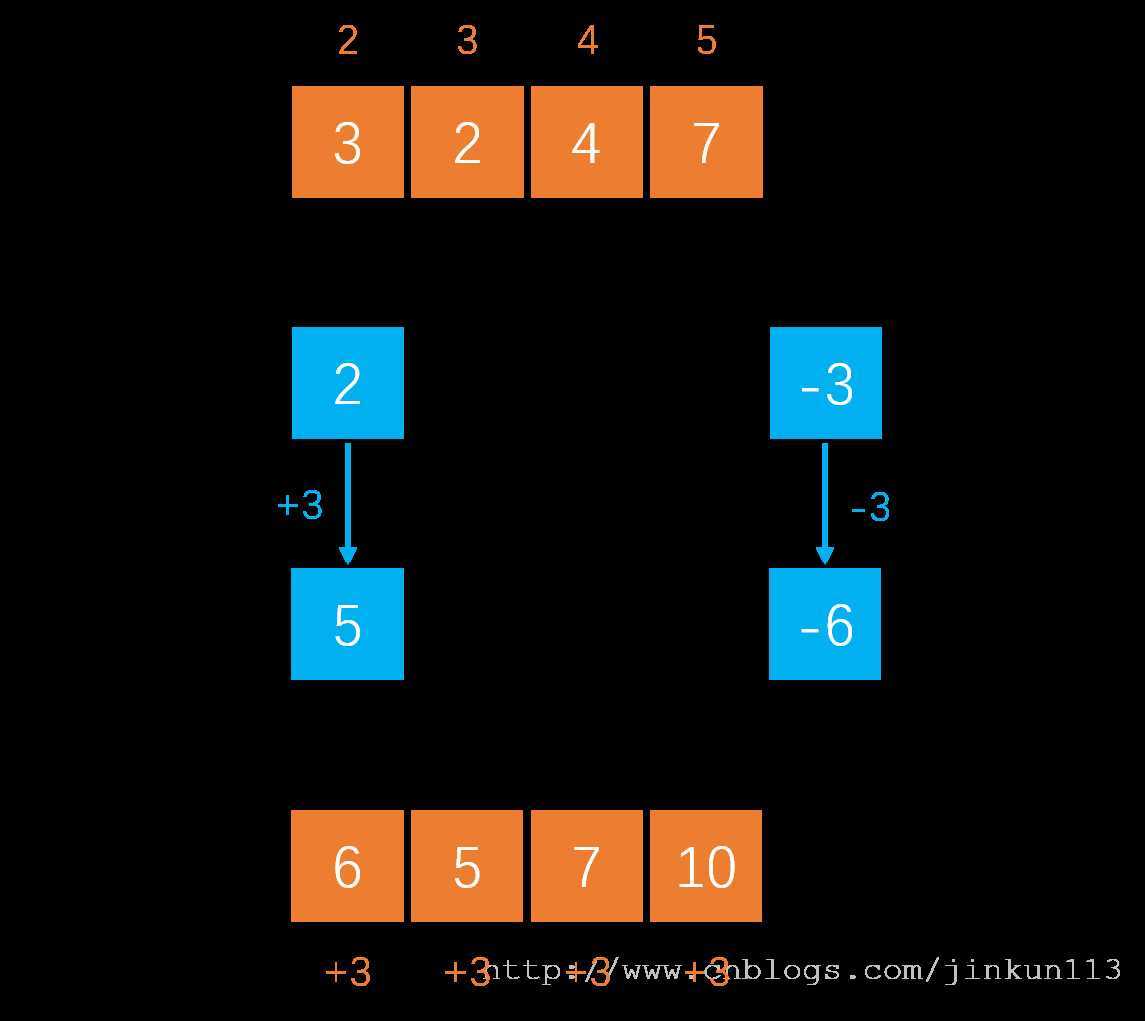
是不是很神奇呢?修改的方式很简单,如果修改区间为 [l, r],则对 b[l] += p, b[r + 1] -=p,具体就不解释原因了。
不过限定条件也体现出了这种方式的不足:差分数组相当于提供了一个临时的方舱医院,需要时间搭建,但一旦搭建好了就能很快收容大量病人,而等疫情结束后再拆除;普通医院是现成的,但床位不够效率不高,然而适用于平常的各种疑难杂症,可以随时收治(好像也不是很恰当、)。
所以如果遇到修改操作和查询操作交替出现的情况,差分数组的便捷则完全体现不出,需要反反复复地在原数组和差分数组之间转化,那和直接枚举的效率不相上下。但同时出现两种操作显然是更符合现实情况的,而要解决这种问题,树状数组和线段树(请参见:)都是很棒的方法,它们适用范围更广于差分数组,但是搭建起来,尤其是线段树,则较为麻烦。
3、多维前缀和
原文:https://www.cnblogs.com/jinkun113/p/12879719.html