线性代数的本质(4)——矩阵乘法与复合变换

4.1 复合变换

在矩阵与线性变换这一节内容中，我们知道了矩阵与线性变换中的对应关系，试想一下，矩阵求逆，其实也是一种变换，就是将变换后的基向量还原为初始态。

ok，做了一次变换之后仍然想做变换，如先将整个平面逆时针旋转90度再做剪切变换，会发生什么？这样从头到尾的总体作用效果就是进行另外一个线性变换。我们将这个新的变换称为两个独立变换的“复合变换”。

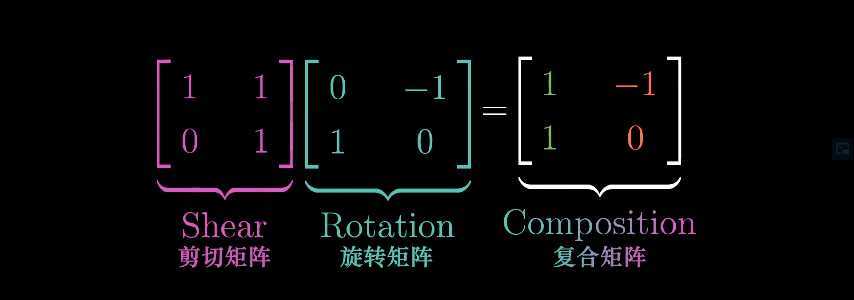
此时这个矩阵捕捉到了逆时针旋转+剪切的总体效应，该矩阵就是一个单独的作用，而不是两个顺序作用的合成。 无论选择什么向量，采用先旋转后剪切变换&对应的符合变换后的作用效果是一致的，我们用数值的方式进行表达如下：

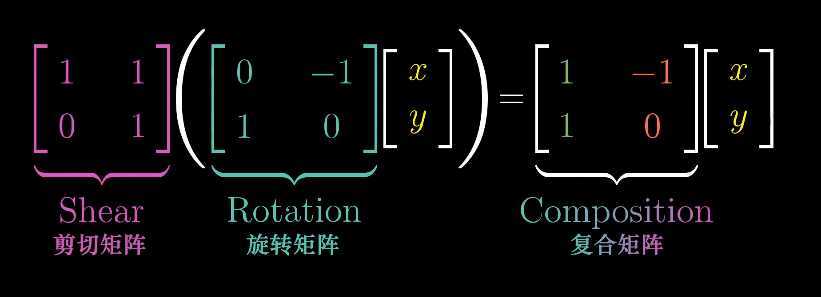
可以得出：两个矩阵相乘，可以表示就是两个线性变换相继作用，需要注意的是，线性变换的作用顺序是从右向左

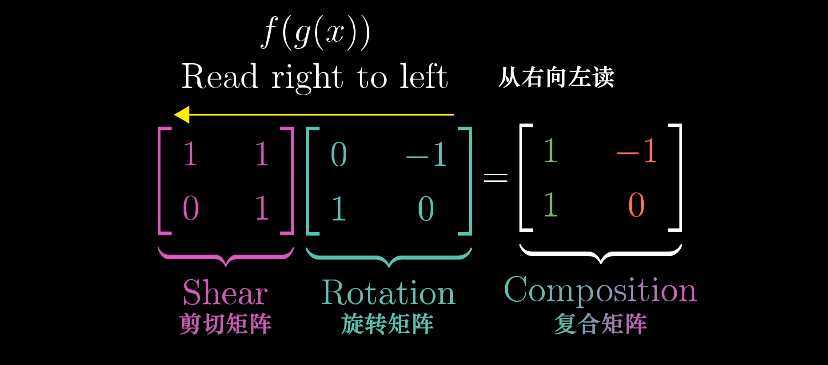
这样类似复合函数 ,也是从里向外读。

4.2 计算复合矩阵

（一）特例

我们同样可以采用追踪基向量的落脚点来描述及计算这个“复合变换”。

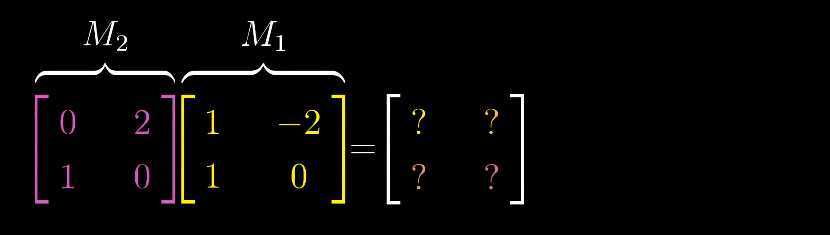
就需要我们计算出基向量 变换后的位置是什么？首先M1表示基向量经过变换后的位置。

• 基向量 ,然后经过 的变换后落在了什么位置？ 

   

• 基向量 ,然后经过 的变换后落在了什么位置？

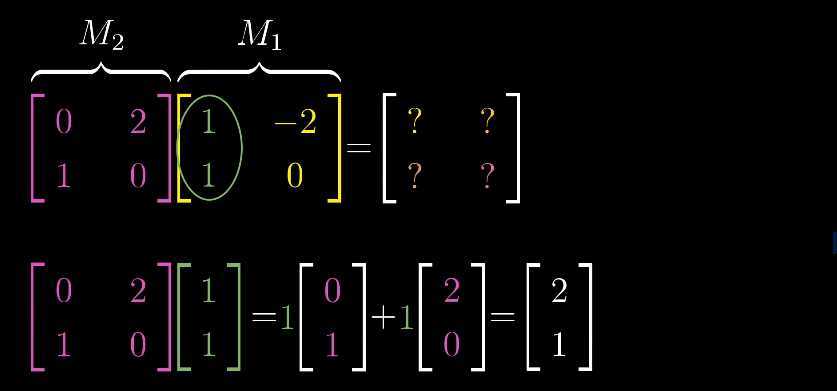
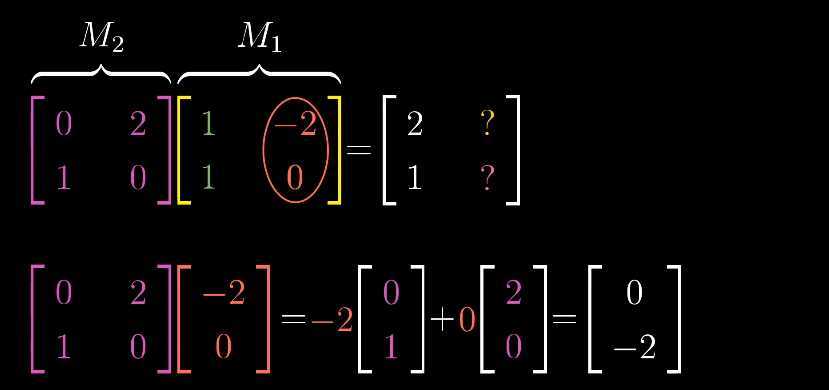
因此：

这个方法具有普适性

（二）一般化计算复合矩阵

4.3复合运算的运算规律

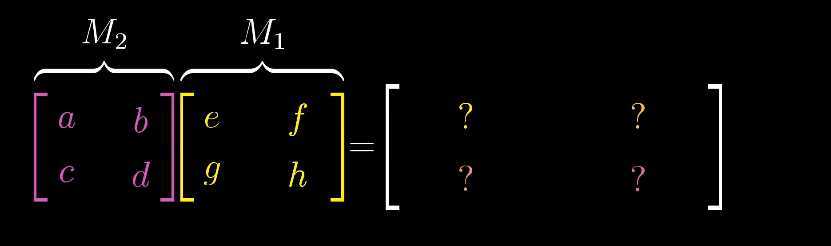
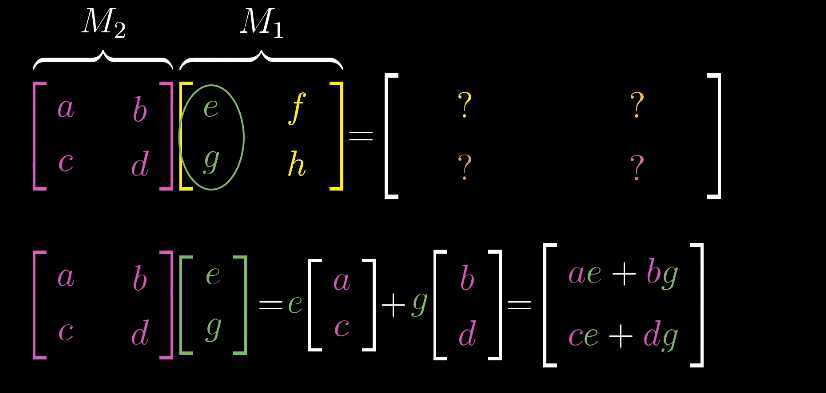
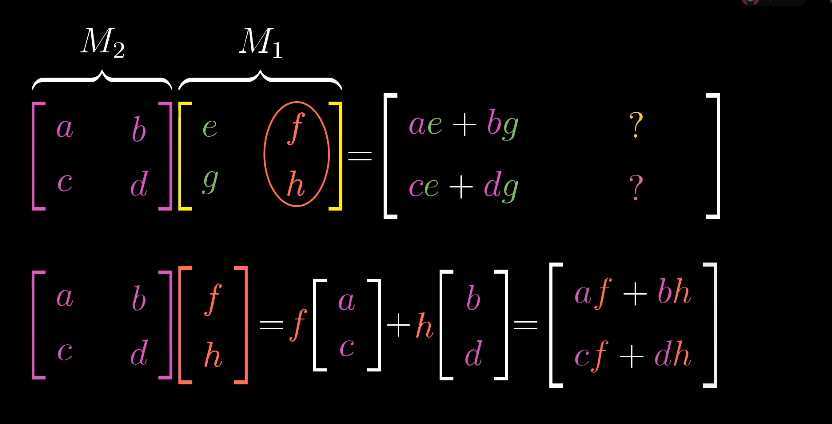
（一）复合运算不满足交换律，一般地，

eg:

（二）复合运算满足结合率，

一般地，

从数值角度证明非常麻烦，如果我们从变换的角度来证明则变得非常显然：

,变换的作用顺序：首先应用C变换和B变换，然后应用A变换

,变换的作用顺序：先应用C变换，然后应用B变换和A变换

4.4 三维空间中的复合变换

同样我们只需要追踪基向量变换后的位置即可。同样地，三维空间中的变换由基向量 的落脚点完全决定,仅仅用9个数字就可以完全描述这个线性变换。 对于任意向量做线性变换，仍然体现的是向量的“缩放”思想及向量相加。

类似这样的变换

，在计算机图像处理、机器人学中有这非常重要的作用。

4.5 总结

1）两个矩阵相乘，可以表示就是两个线性变换相继作用

2）矩阵相乘，对应的线性变换作用顺序是从右向左

3) 三维空间中的变换与二维空间中的变换类似。而三维变换在计算机图像处理、机器人学中有着重要的作用.

线性代数的本质(4)——矩阵乘法与复合变换

原文：https://www.cnblogs.com/wkfvawl/p/12883898.html