图总结

一、思维导图

二、概念笔记

1、深度优先遍历

深度优先遍历的过程是从图中的某个初始点v出发,首先访问初始点v,然后选择一个与顶点v相邻且没被访问过的顶点w,以w为初始顶点,再从它出发进行深度优先遍历,直到图中与顶点V邻接的所有顶点都被访问过为止。

2、广度优先遍历

广度优先遍历的过程是首先访问初始点U,接着访问顶点V的所有未被访问过的邻接点v0,v1,...,vt然后再按照v0,v1,...,vt的次序访问每一个顶点的所有未被访问过的邻接点依此类推，直到图中所有和初始点V有路径相通的顶点都被访问过为止。

3、最小生成树

图的所有生成树中具有边上的权值之和最小的树称为图的最小生成树。按照生成树的定义，n个顶点的连通图的生成树有n个顶点、（n-1）条边。

4、Prim算法求最小生成树

假设G=(V,E)是一个具有n个顶点的带权连通图.T=(U,TE)是G的最小生成树，其中U是T的顶点集,TE是T的边集,则由G构造从起始点U出发的最小生成树T的步骤如下:
(1)初始化U=(v},以V到其他顶点的所有边为候选边。
(2)重复以下步骤(n- 1)次,使得其他(n 1)个顶点被加入到U中。
①从候选边中挑选权值最小的边加人TE,设该边在V-U中的顶点是k,将k加入U中;
②考查当前V-U中的所有顶点j，修改候选边,若(k,j)的权值小于原来和顶点j关联的候选边，则用(k,j)取代后者作为候选边。

5、Kruskal算法求最小生成树

假设G=(V,E)是一个具有n个顶点的带权连通无向图,T=(U,TE)是G的最小生成树，则构造最小生成树的步骤如下:
(1)置U的初值为V(即包含有G中的全部顶点),TE的初值为空集(即图T中的每一个顶点都构成一个分量)。
(2)将图G中的边按权值从小到大的顺序依次选取,若选取的边未使生成树T形成回路，则加入TE,否则舍弃,直到TE中包含(n- 1)条边为止。

6、dijkstra算法求最短路径

基本思想是，设G=(V,E)是一个带权有向图，把图中的顶点集合V分成两组。
第1组为已求出最短路径的顶点集合(用S表示，初始时S中只有一个源点，以后每求得一- 条最短路径v...u,就将顶点u加入到集合S中,直到全部顶点都加入到S中,算法就结束了)；
第2组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第2组的顶点加人S中。

7、AOE网与拓扑排序

在AOE网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列，由AOE网构造拓扑序列的过程叫做拓扑排序。AOE网的拓扑序列不是唯一的，满足上述定义的任一线性序列都称作它的拓扑序列。

三、疑难问题

1、问题：

在学习完普里姆算法和克鲁斯卡尔算法后，总是分不清两个算法的区别，以至于在很多问题中，我用两个算法得到的最小生成树是一摸一样的。　　

2、解决：

在看了很多博客和视频后我得到了两个算法的区别：在于Prim算法是挨个找，而Kruskal是先排序再找。
Prim算法最小生成树查找过程：

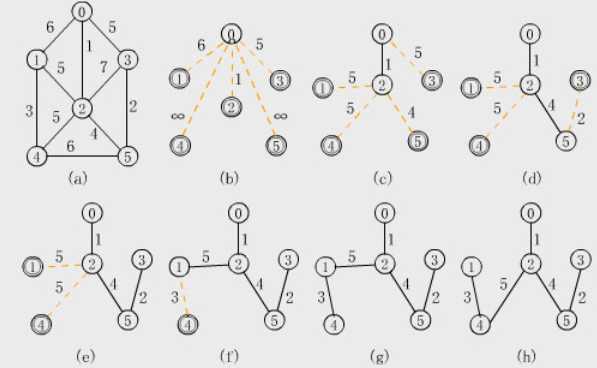
Kruskal算法与Prim算法的不同之处在于，Kruskal在找最小生成树结点之前，需要对所有权重边做从小到大排序。将排序好的权重边依次加入到最小生成树中，如果加入时产生回路就跳过这条边，加入下一条边。当所有结点都加入到最小生成树中之后，就找出了最小生成树。

图总结

原文：https://www.cnblogs.com/zx224569/p/12883885.html