该系列为DR_CAN自动控制原理视频笔记，详见https://space.bilibili.com/230105574
由于笔者水平有限，文中难免存在一些不足和错误之处，诚请各位批评指正。

1 换一种模式的体重模型

与上一个模型不同，这里我们的输入由 \(E_i-E_a - ac\) 变为 \(E_i-E_a\) ，并引入系统扰动这一概念，我们令系统扰动（disturbance） \(d = -ac\) 。通过调整系统输入我们得到了一个新的传递函数：

2 应用比例控制器

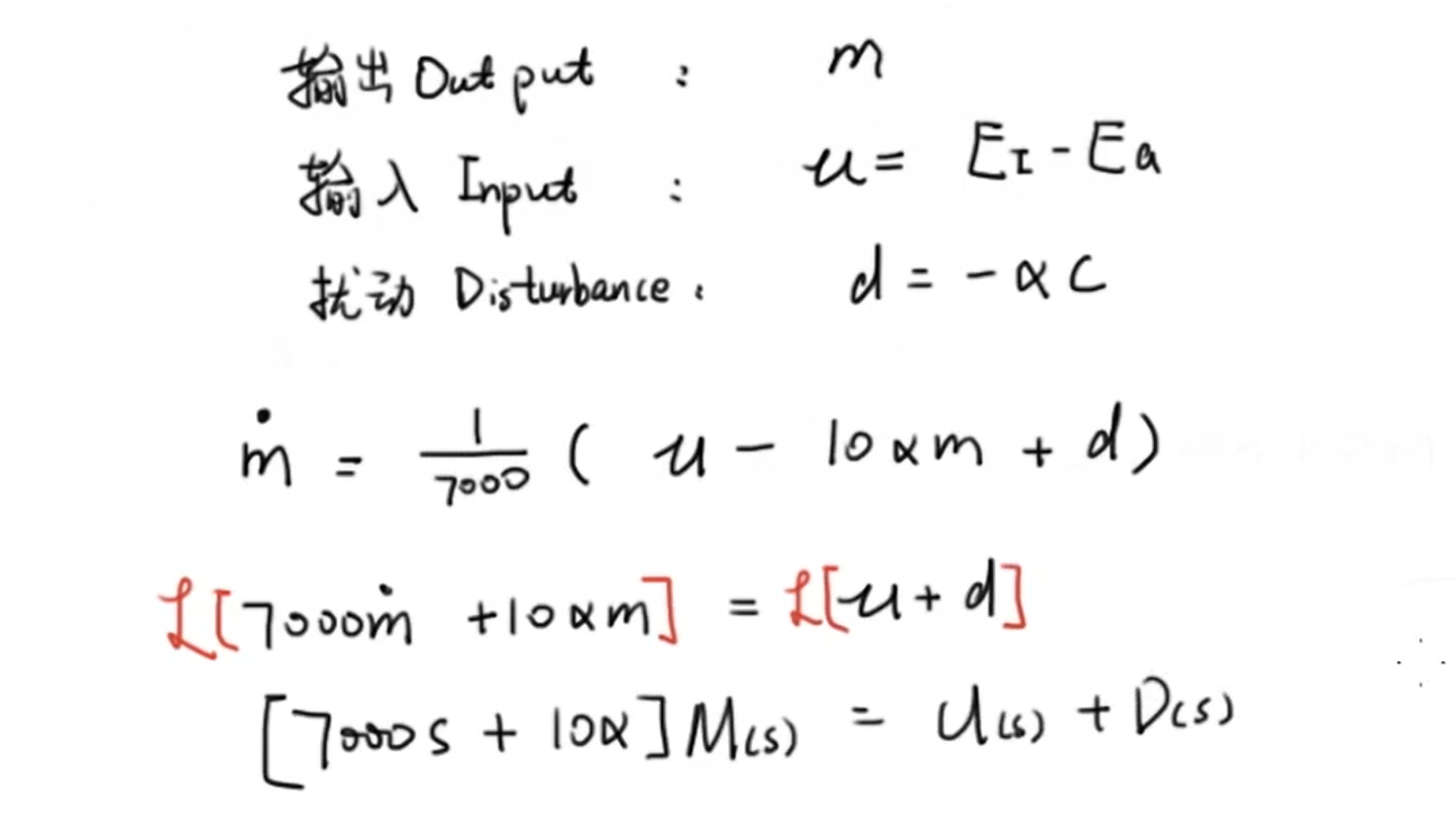
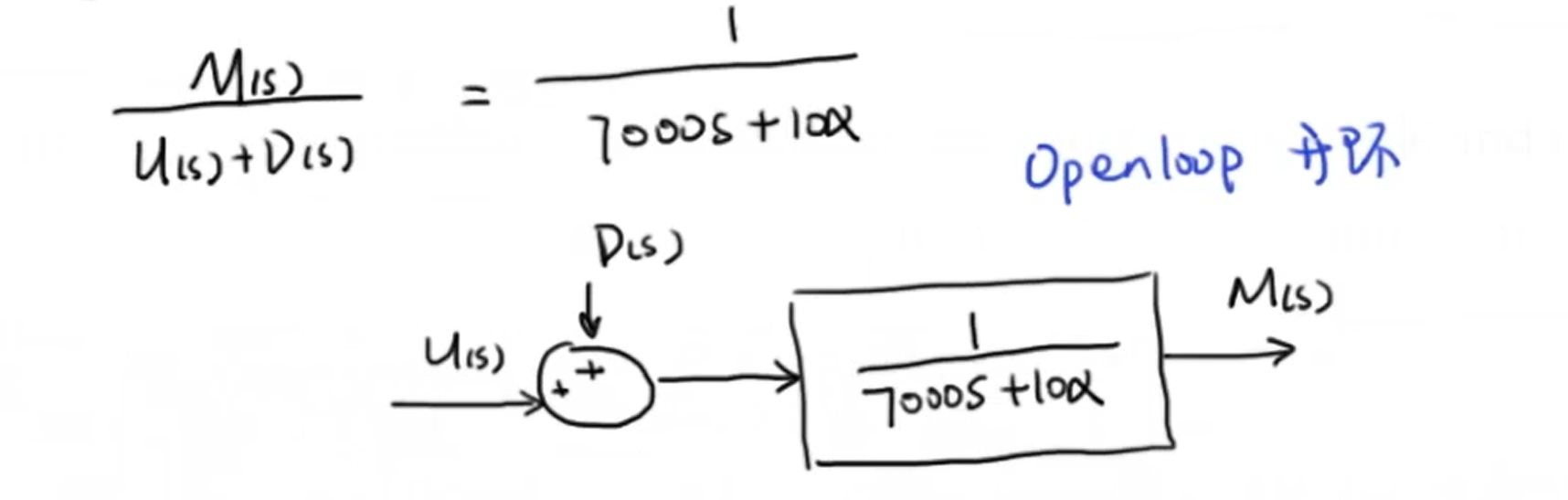
应用比例控制器这个东西都知道就不多说了：

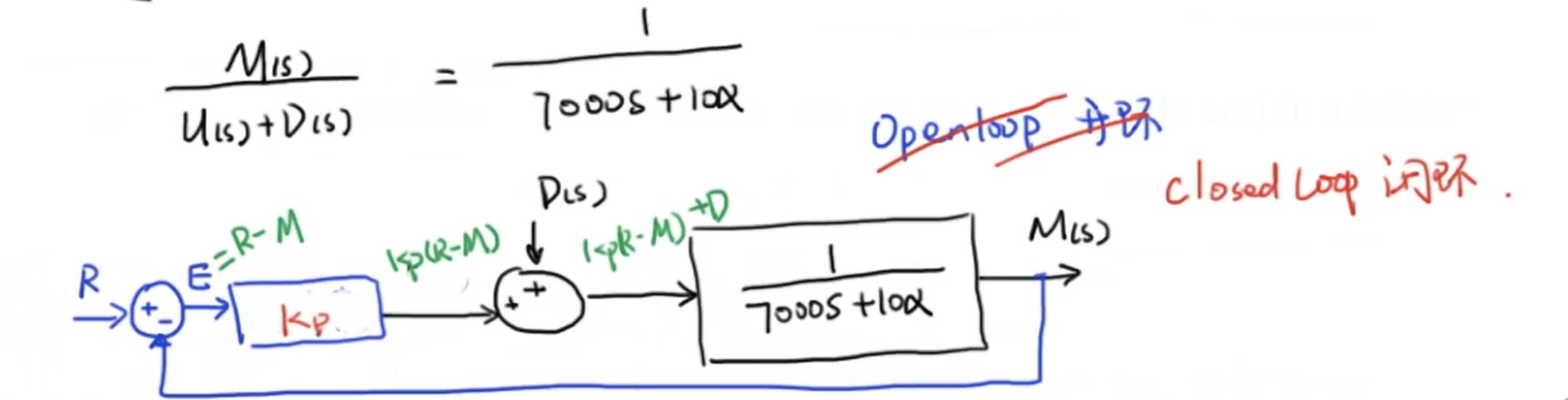
有了比例控制的环节，我们写出现在的闭环系统响应：

经过移项，把M都放到等式的一边：

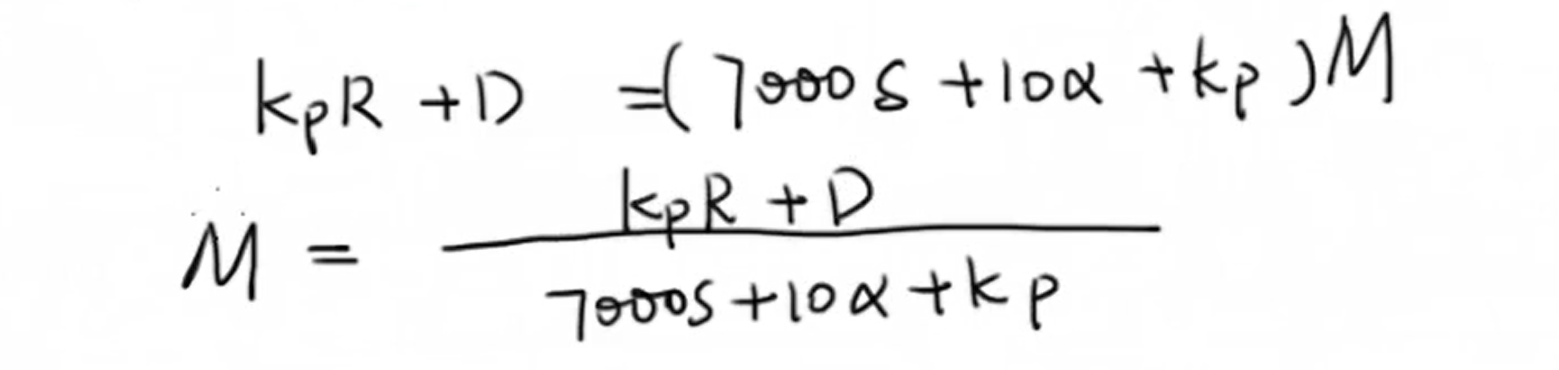
通过分析这个表达式的极点，我们就可以得到这个闭环系统的稳定性。有一个结论，就是如果R和D是稳定的，他们就不会对M的稳定性产生影响，通过将这个等式中的D和R进行拉普拉斯变换，可以得到：

其实比例控制器给闭环系统输出响应带来了一个极点 \(s = 0\) ，这个极点时域情况下为一个常数，并不影响变化趋势也就是稳定性。我们关注另一个极点，不难发现，当 \(K_p > -10\alpha\) 时极点位于虚轴左侧。

3 在Simulink中搭建与分析

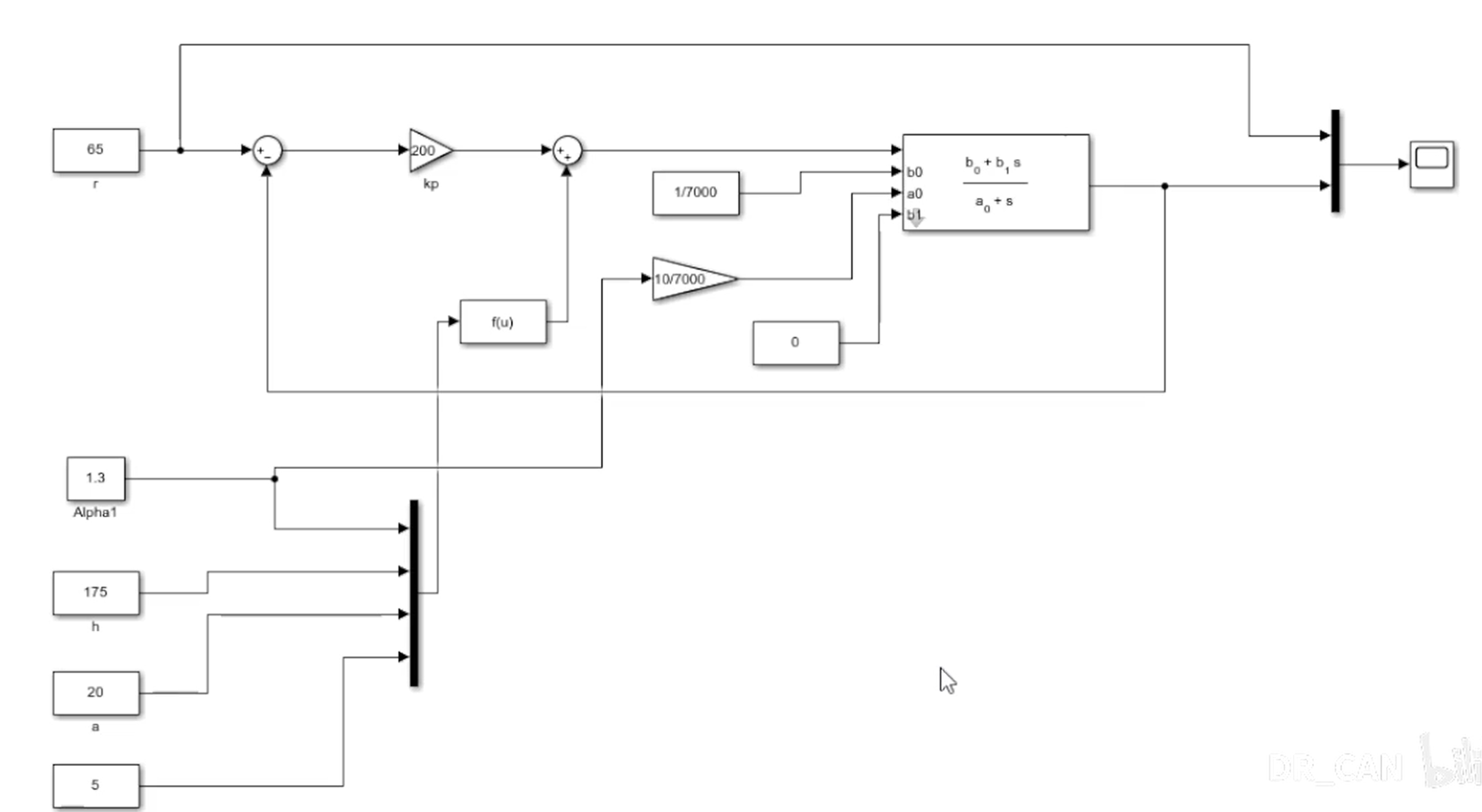
经过运行我们发现Kp在200的情况下系统可以收敛，但却很难收敛到期望值，期望值和收敛值之间会存在稳态误差（Steady State Error）：

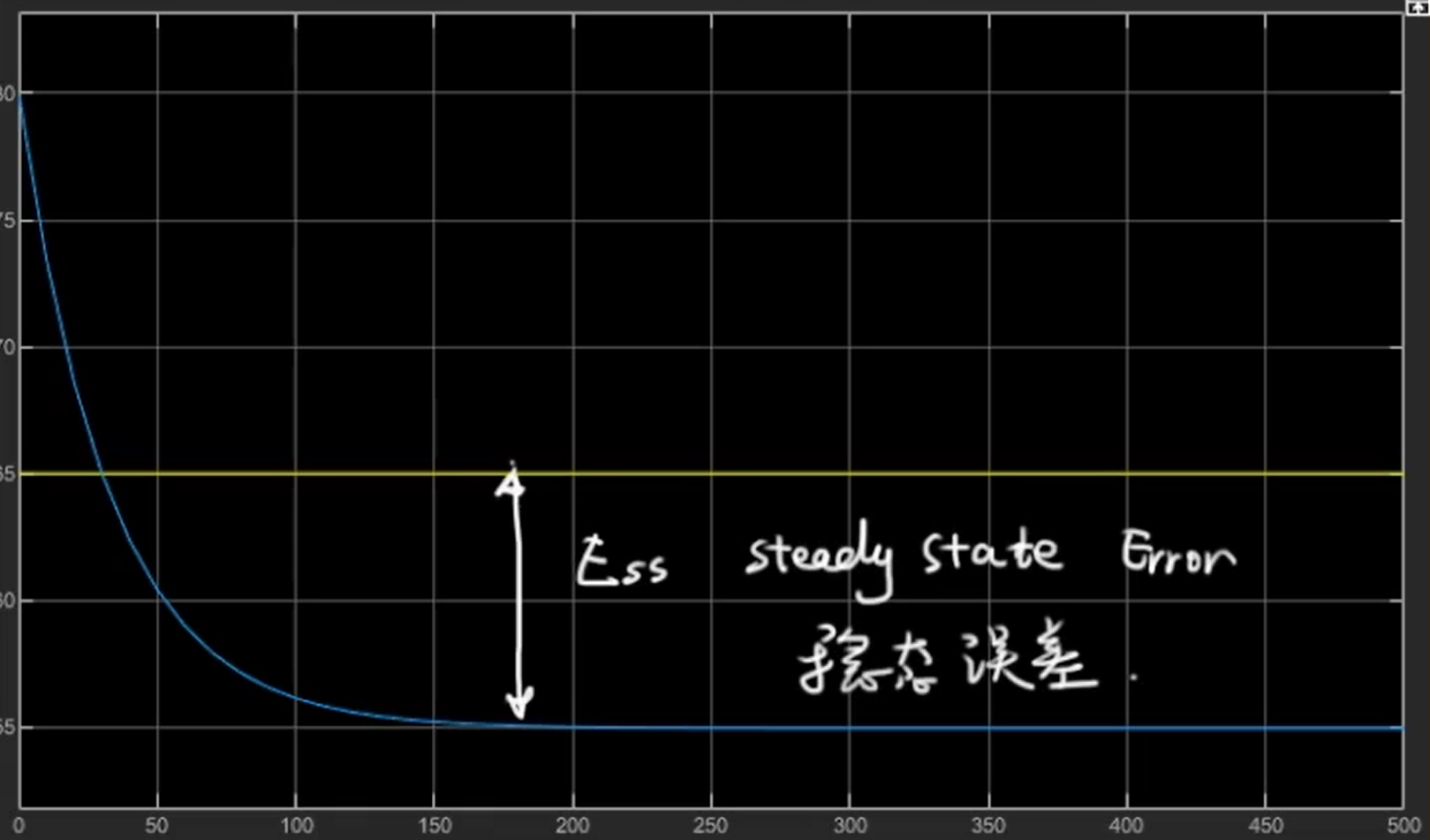
这个稳态误差是由系统的特性引起的，在下一篇中会详细分析稳态误差的产生以及消除方法。

（三）系统分析实例② 比例控制

原文：https://www.cnblogs.com/HongxiWong/p/12885410.html