蒙特卡洛模拟

2020年5月13日，沈阳航空航天大学电子信息学院研究生入学考试复试口试题目

题目描述：

A 是 0 到 0.2 之间的数，B 是 0 到 0.8 之间的数。求 B 比 A 大的概率是多少？

解析解

题目没有说明，但是可以分析可知，A 和 B 都应该属于均匀分布（uniform），也即

因为

易知

凭借直觉容易得出 \(P(B > A | B \leq 0.2) = 0.5\) 的结论，但是如何证明呢？设 \(B‘ \sim uniform(0, 0.2)\)，则问题转化为求 P(B‘ > A)。因为 A 和 B‘ 服从同一均匀分布，所以B‘大于A的概率应为0.5

所以

近似解

使用蒙特卡洛模拟法可以得到该题目的近似解，按照均匀分布来生成 A 和 B，然后比较大小得到频率。模拟 100 万次的效果如下图所示。

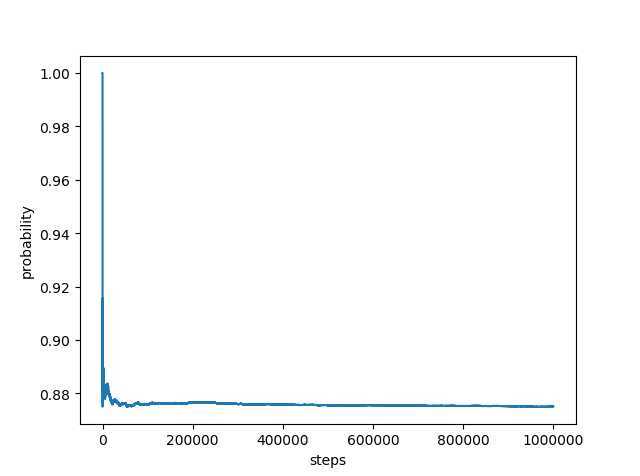
程序得出的频率为 0.875122，误差在万分之一上下。

附录

蒙特卡洛模拟的程序如下：

# coding=utf-8

import numpy as np
from matplotlib import pyplot as plt


def generate(beg, end):
    return np.random.uniform(beg, end)


if __name__ == ‘__main__‘:
    iteration = 1000000 # 100w 次模拟

    step = 1
    counter = 0
    x, y = list(), list()

    plt.xlabel("steps")
    plt.ylabel("probability")

    for i in range(iteration):
        sample1 = generate(0, 0.2)
        sample2 = generate(0, 0.8)

        if sample1 < sample2:
            counter = counter + 1

        if i % step == 0:
            x.append(i)
            p = counter / (i+1)
            y.append(p)
            print(p)

    plt.plot(x, y)
    plt.show()

蒙特卡洛模拟

原文：https://www.cnblogs.com/fengyubo/p/12885383.html