打破认知观的一节,之前学习行列式都是从逆序数开始学起,学习行列式的性质,做大量计算练习,这里直接告诉我们行列式的值代表面积/体积,建立了与矩阵、线性变换的联系,真的是一语惊醒梦中人!
(1)行列式的意义
线性变换会对空间进行挤压或者拉伸,我们通过追踪空间基向量的变换,来查看单位面积(二维)/单位体积(三维)的面积或者体积缩放比例,而这个缩放比例,对应的就是行列式的值。
(2)我们就建立了线性变换、矩阵、行列式之间的关系。
(3)行列式值为0 表示将空间压缩到更低的维度
(4) 矩阵的列向量线性相关行列式的值0
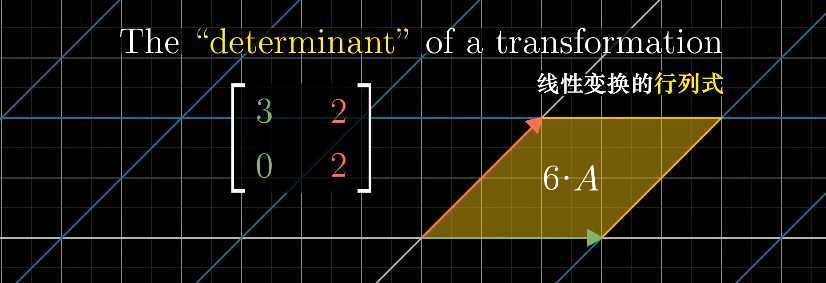
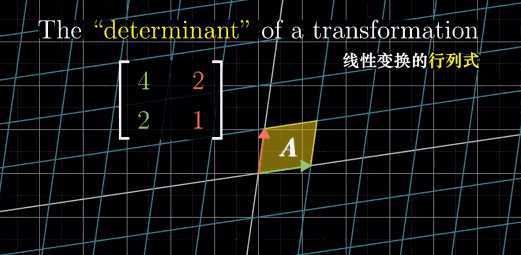
在线性变换的时候,有的线性变换起到空间挤压的作用,有的线性变换起到了空间拉伸的作用,那么测量变换到底对空间拉伸或者挤压了多少。 我们可以追踪变换后基向量的面积大小。从这个层面上,建立了 “矩阵与行列式之间的关系”。

行列式的意义--面积的缩放发小
首先我们看一下剪切变换带来的面积变化?经过计算可得,剪切变换不仅带来了空间的挤压,而且保持面积不变。(如下图)
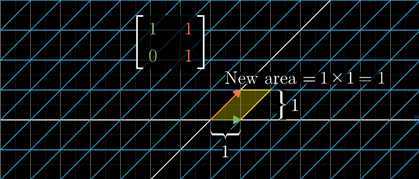
剪切变换面积保持不变
我们只要追踪基向量构成的单位面积的变化,因为其他区域面积变化的比例大小与单位面积变化的比例保持一致,这样就可以知道空间中任意区域面积变化的比例,这是因为线性变换保持“网格线平行且等距变换”。
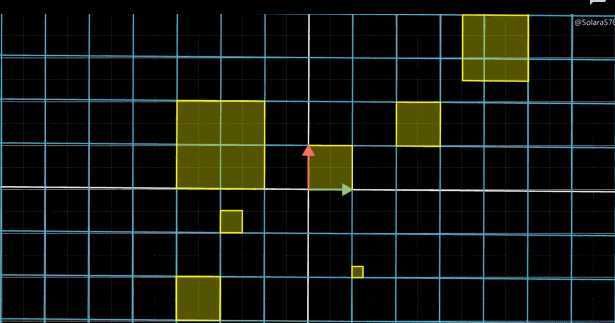
任意平行区域的面积缩放比例--线性变换的性质相关
对于空间中任意区域的面积,借助微积分的思想,我们可以采用足够小方格来逼近区域的面积。
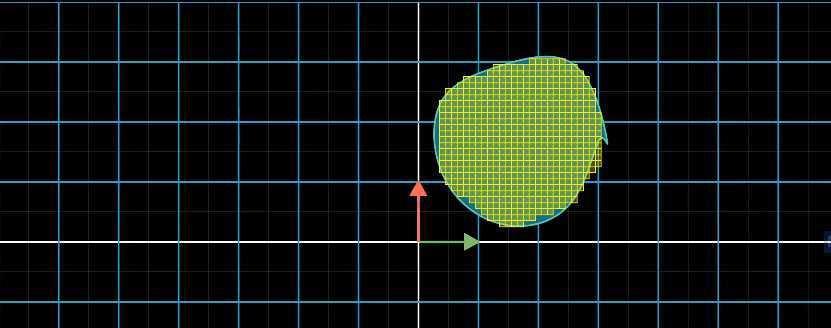
不规则区域面积求解
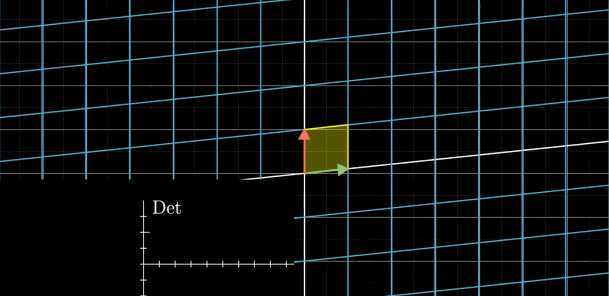
只要检验行列式的值是否为0,就能够判断线性变换是否将空间挤压到更小的维度。
挤压为一条直线

挤压为一个点
我们采用基向量来描述:
这样的结果就是空间取向发生了变换,即将整个空间翻转了一遍。(如下图)

为什么负值与空间取向有关?
以二维空间为例,基向量保持不变,基向量
逆时针逐渐靠近
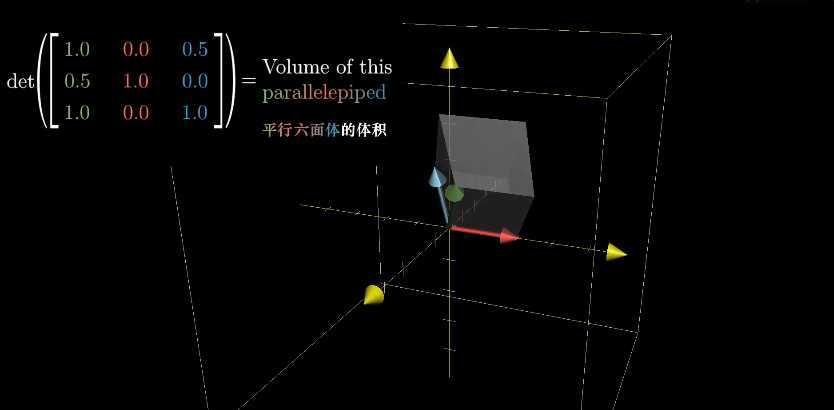
三维空间中行列式的值代表着体积的缩放比例,我们关注的是单位立方体进行线性变换后的体积变化,对应行列式的值表示对应平行六面体的体积。
行列式为0,意味着空间被压缩为一个平面、一条直线、甚至是一个点。
矩阵线性相关 行列式的值0 ;
三维空间坐标系我们默认采用右手法则,(食指表示 ,中指表示
,拇指表示
)

右手法则
当空间变换后,仍然采用(食指表示,中指表示
,拇指表示
),这时候就只能用左手法则表示,这就意味着空间取向发生了翻转,行列式的值为负。
这个公式直观的理解就是:
,表示底为
,高为
的平行四边形的面积
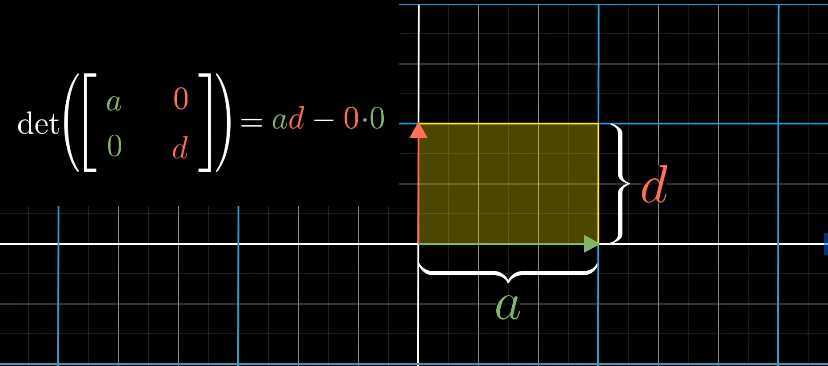
,仍然表示底为
,高为
的平行四边形的面积
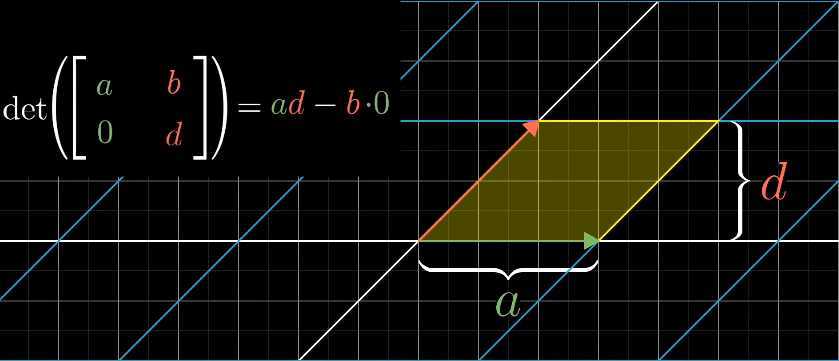
当行列式斜对角线的元素及
均不为0时,bc项就会告诉平行四变形在对角方向拉伸或者压缩了多少,bc项代表的含义如下图:
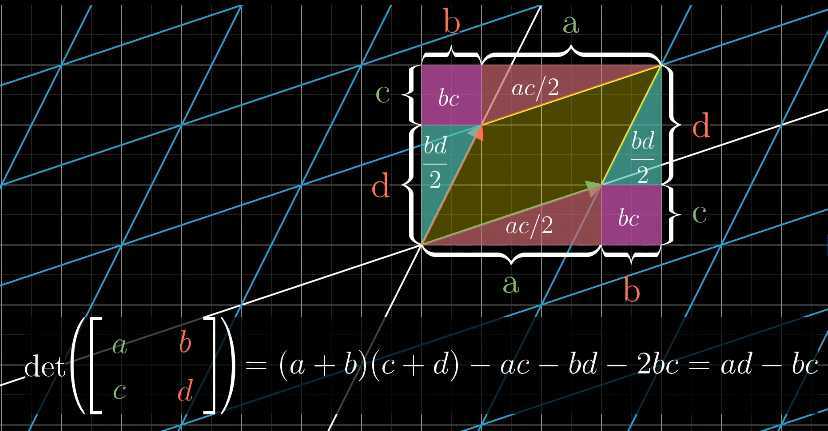
可以看出,行列式的值与面积有着紧密的联系。
用计算行列式的值来解释等式为什么成立会比较繁琐,我们采用行列式的几何意义来解释将会比较简单:
显然两者变换的方式是等价的,带来的面积缩放比例也是一致的,因此等式左右两边成立。
(1)行列式的意义
线性变换会对空间进行挤压或者拉伸,我们通过追踪空间基向量的变换,来查看单位面积(二维)/单位体积(三维)的面积或者体积缩放比例,而这个缩放比例,对应的就是行列式的值。
(2)我们就建立了线性变换、矩阵、行列式之间的关系。
(3)行列式值为0 表示将空间压缩到更低的维度
(4) 矩阵的列向量线性相关行列式的值0
原文:https://www.cnblogs.com/wkfvawl/p/12886446.html