所谓的线性表是由n个类型相同数据结构的有限序列(见下图)
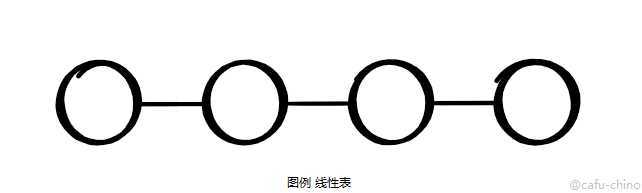
线性表的特点
- 同一性
- 有穷性
- 有序性
typedef struct
{
ElemType elem[MAXSIZE]; //线性表的占用的存储空间
int last;//记录表中最后一个元素所在的位置
}Seqlist;
这个比较简单,不做过多的解释直接上代码
#include <bits/stdc++.h>
using namespace std;
const int MAXSIZE = 100;
typedef struct
{
int elem[MAXSIZE];//ElemType
int last;
}Seqlist;
/*初始化线性表*/
bool InitList(Seqlist *l){
memset(l->elem,0,sizeof(l->elem));
l->last=-1;
return true;
}
/*删除指定位置i开始的k个元素*/
bool DelList(Seqlist *l,int i,int k){
if(i < 1 || i > l->last+1){
cout << "非法删除位置" << endl;
return false;
}
else if(k <= l->last+1-i){
for(int j=i-1; j < k+i-1; j++)
l->elem[j]=0;
for(int j=i-1; j < l->last-k+1; j++)
l->elem[j]=l->elem[j+k];
l->last-=k;
return true;
}
else{
for(int j=i-1; j <= l->last; j++)
l->elem[j]=0;
l->last=i-2;
return true;
}
}
/*输出线性表中所有元素*/
void PrintList(Seqlist *l){
for(int i=0; i <= l->last; i++)
cout << l->elem[i] << " ";
}
/*查找线性表中元素所在位置*/
int Locate(Seqlist L,int e){
int i=0;
while (i < L.last && L.elem[i] != e)
i++;
if(i < L.last)
return i+1;
else
return -1;
}
int main(){
Seqlist *l;
Seqlist _list;
l=&_list;
if(InitList(l)){
int i,k,book=0;
cin >> i >> k;
while(cin >> l->elem[book]){
book++;
}
l->last=book-1;
if(DelList(l,i,k)){
cout << "delete success" << endl;
PrintList(l);
}
else{
cout << "删除失败" << endl;
PrintList(l);
}
}
else
cout << "初始化失败" << endl;
system("pause");
return 0;
}
我们来讲讲这种存储结构的优缺点
优点
- 方便读取某个位置上元素
缺点
- 线性表长度需在确定,空间有限
- 插入删除某个元素效率低
即每个结点中只存储数据和下一个结点地址(见下图),故只能从头开始依次访问链表中的节点
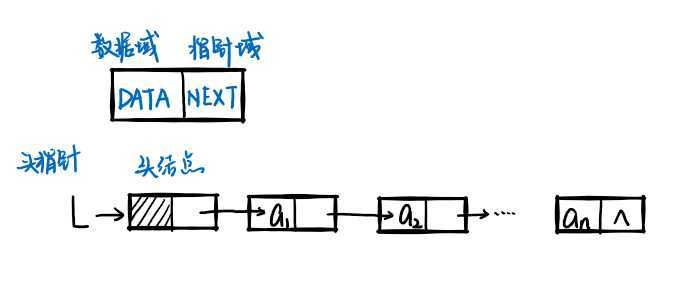
访问第一个存放数据的结点方法p=L->next
struct Node{
ElemType data;
struct Node *next;
}Node,*Linklist;
#include <bits/stdc++.h>
using namespace std;
struct Node{
int data;//ElemType
struct Node *next;
}Node,*Linklist;
/*初始化链表*/
void InitList(Linklist *L){
*L=(Linklist)malloc(sizeof(Node));
*L->next = NULL;
}
/*头插法建立链表*/
void CreatFromHead(Linklist L){
Node *s;
int num;//每个节点的数据,可以是其他数据类型
while (cin >> num)
{
s=(Node *)malloc(sizeof(Node));
s->data=num;
s->next=L->next;
L->next=s;
}
}
/*尾插法建立链表*/
void CreatFromTail(Linklist L){
Node *s,*r;
r=L;
int num;//每个节点的数据,可以是其他数据类型
while (cin >> num)
{
s=(Node *)malloc(sizeof(Node));
s->data=num;
r->next=s;
r=s;
}
}
/*求链表的长度*/
int ListLength(Linklist L)
{
Node* p=L->next;
int i=0;
while(p != NULL){
i++;
p=p->next;
}
return i; //返回链表长度
}
/*查询第i个节点*/
Linklist Query(Linklist L,int pos){
if(pos <= 0 && pos > ListLength(L))
return NULL;
Node* p=L;
int j=0;
while((p->next != NULL) && (j != pos)){
p=p->next;
j++;
}
return p;
}
int main(){
Node *L;
InitList(&L);
return 0;
}
即单链表每个节点中增加了存储前继指针域(用于存放前继结点的所在地址)(见下图),解决了单链表不能任意结点访问所有表中的元素的问题
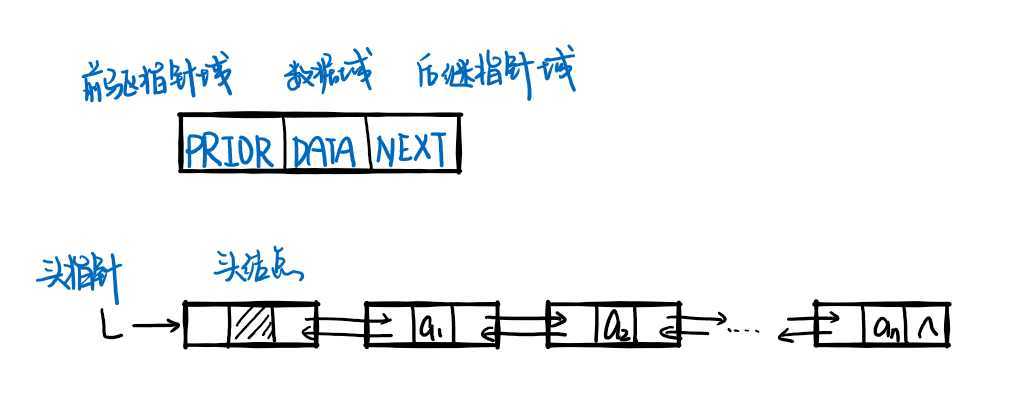
struct Node{
ElemType data;
struct Node *next ,*prior;
}Node,*Linklist;
这里直接展示代码了,我们来讲一个应用——利用循环表(或者链表)输出杨辉三角形(过程见下图)
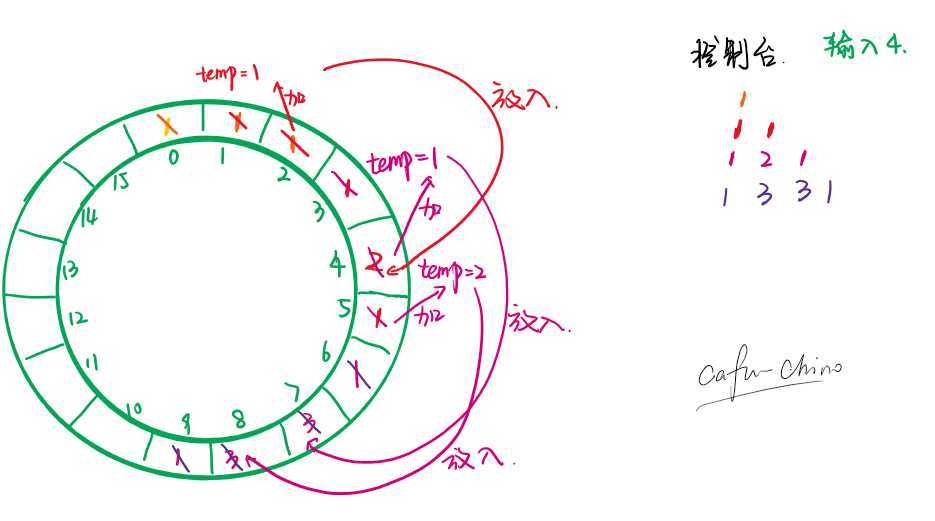
我们假设需要输出4行
#include <bits/stdc++.h>
using namespace std;
const int MAXSIZE=50;//设定顺序表最大的顺序表,输出的杨辉三角的每层元素不能超过该最大长度-1
typedef struct{
int element[MAXSIZE];
int front;//队头
int rear;//队尾
}SeqQueue;
void InitQueue(SeqQueue *Q){
Q->front=Q->rear=0;
}
bool IsEmpty(SeqQueue *Q){
if(Q->front == Q->rear)
return true;
return false;
}
void GetHead(SeqQueue *Q, int *x)//取对头元素
{
if (Q->front == Q->rear)
return ;
*x = Q->element[Q->front];
return ;
}
void EnterQueue(SeqQueue *Q,int x){
if((Q->rear+1)%MAXSIZE == Q->front)
return ;
Q->element[Q->rear] = x;
Q->rear = (Q->rear + 1) % MAXSIZE;
return ;
}
void DeleteQueue(SeqQueue *Q,int *x){
if (Q->front == Q->rear)
return ;
*x = Q->element[Q->front];
Q->front = (Q->front + 1) % MAXSIZE;
return ;
}
void YangHuiTriangle(int N)
{
int n, i, x, temp;
SeqQueue Q;
InitQueue(&Q);
EnterQueue(&Q, 1); /* 第一行元素入队*/
for (n = 2; n <= N; n++) /* 产生第 n 行元素并入队,同时打印第 n-1 行的元素*/
{
EnterQueue(&Q, 1); /* 第 n 行的第一个元素入队*/
for (i = 1; i <= n - 2; i++) /* 利用队中第 n-1 行元素产生第 n 行的中间 n-2 个元素并入队*/
{
DeleteQueue(&Q, &temp);
printf("%d", temp); /* 打印第 n-1 行的元素*/
GetHead(&Q, &x);
temp = temp + x; /*利用队中第 n-1 行元素产生第 n 行元素*/
EnterQueue(&Q, temp);
}
DeleteQueue(&Q, &x);
printf("%d\n", x); /* 打印第 n-1 行的最后一个元素 */
EnterQueue(&Q, 1); /* 第 n 行的最后一个元素入队 */
}
while (!IsEmpty(&Q)) /* 打印最后一行元素 */
{
DeleteQueue(&Q, &x);
printf("%d", x);
}
}
int main()
{
int num;
cin >> num;
YangHuiTriangle(num);
system("pause");
return 0;
}
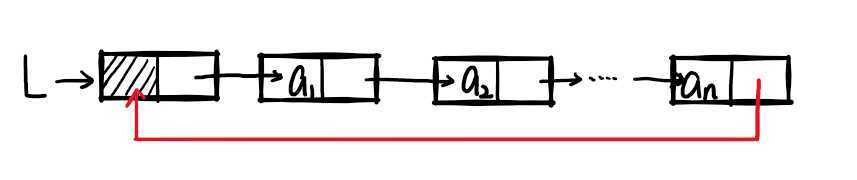
即在单链表的基础上,在其尾结点的指针域指向头结点(形成一个环状的结构)
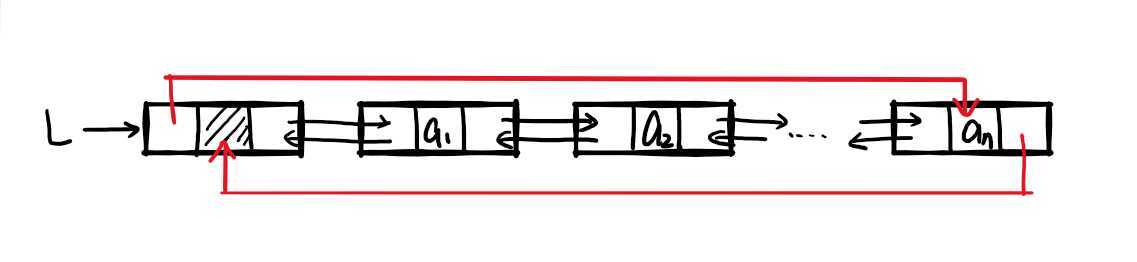
即在双向链表的基础上,在其头结点前继指针域以及尾结点后即指针域分别指向尾结点和头结点(同样形成一个环状结构)
原文:https://www.cnblogs.com/cafu-chino/p/12887210.html