该系列为DR_CAN自动控制原理视频笔记，详见https://space.bilibili.com/230105574
由于笔者水平有限，文中难免存在一些不足和错误之处，诚请各位批评指正。

1 比例控制器的不足

之前提到过，比例控制不能很好的消除系统的稳态误差，因此需要引入积分控制来消除稳态误差。以下是比例控制闭环系统输出的稳态误差推导，之前有详细说过这里不再赘述：

2 设计新的控制器

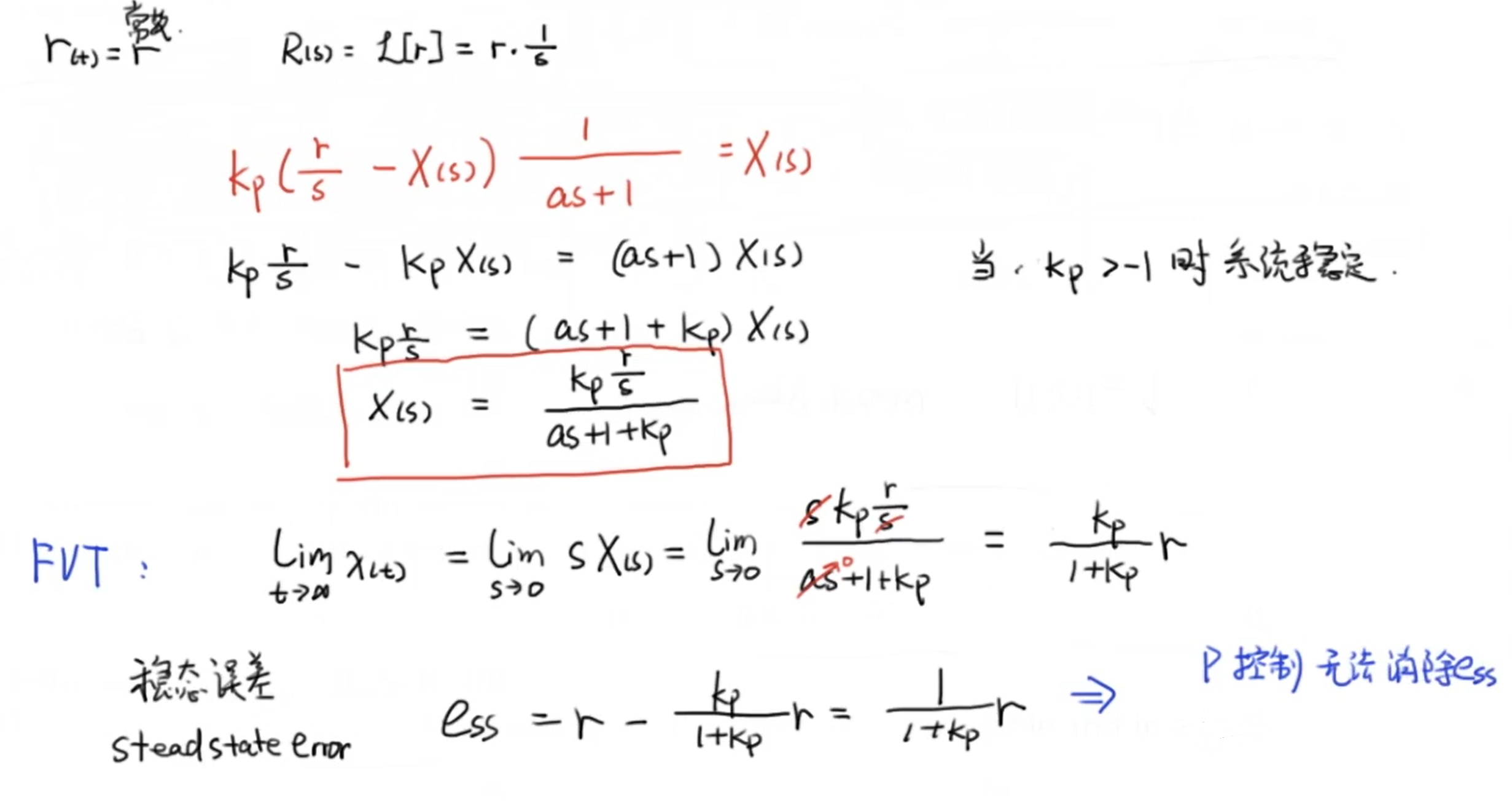
经过推导我们发现仅用比例控制器无法消除稳态误差，因此我们需要设计新的控制器。假设新控制器的传递函数为 \(C(s)\) ，这样我们可以计算出新的稳态误差表达式。并且我们希望新的控制器可以消除稳态误差，也就是令 \(\lim _{t \rightarrow \infty} x_{(t)}=r\) ，其中 \(r\) 为目标值，经过计算我们得到了以下结果：

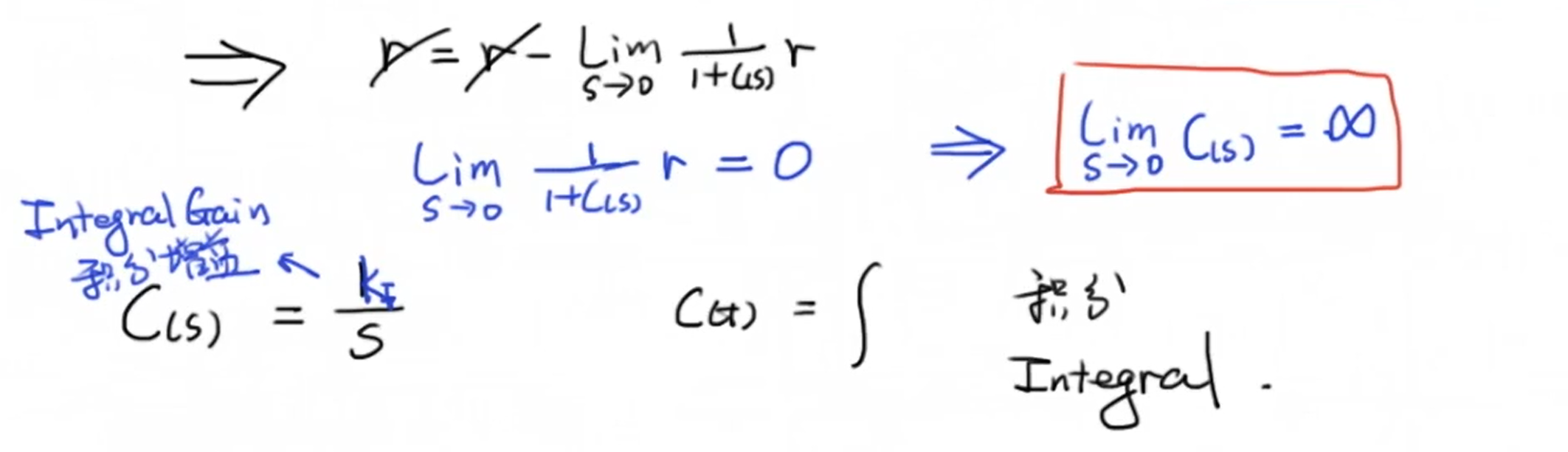
我们发现要想新的控制器可以消除稳态误差，我们需要一个积分过程，为了调节积分控制器的表现，我们在前面乘一个积分增益 \(K_i\) 。接下来我们把 \(C(s)\) 代入上面的系统输出表达式中：

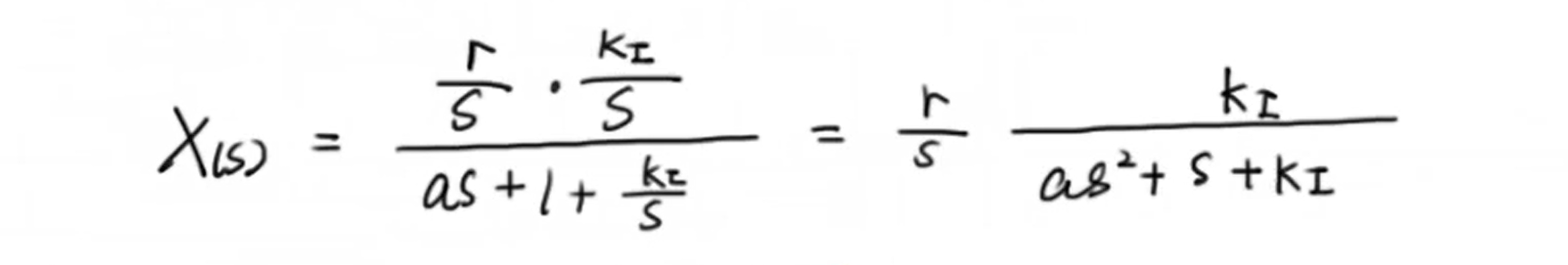
接下来我们把分母乘过去，然后进行拉普拉斯逆变换得到一个微分方程。这时候可以发现这个微分方程变成了一个二阶系统的阶跃响应：

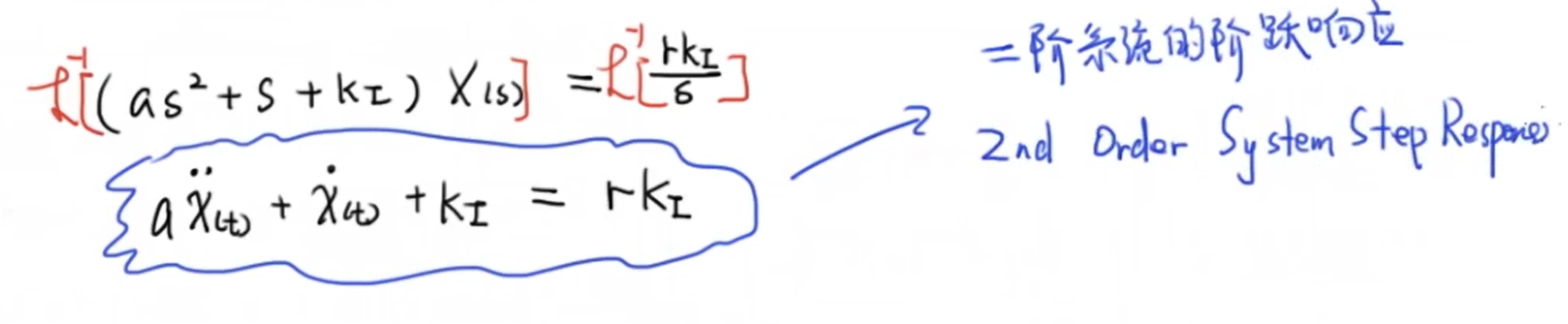
这样，结合二阶系统阶跃响应的有关内容，我们可以很直观的感受到积分增益 \(K_i\) 的变化给系统带来的影响。

3 在Simulink中测试

首先我们分别搭建比例闭环控制和积分闭环控制：

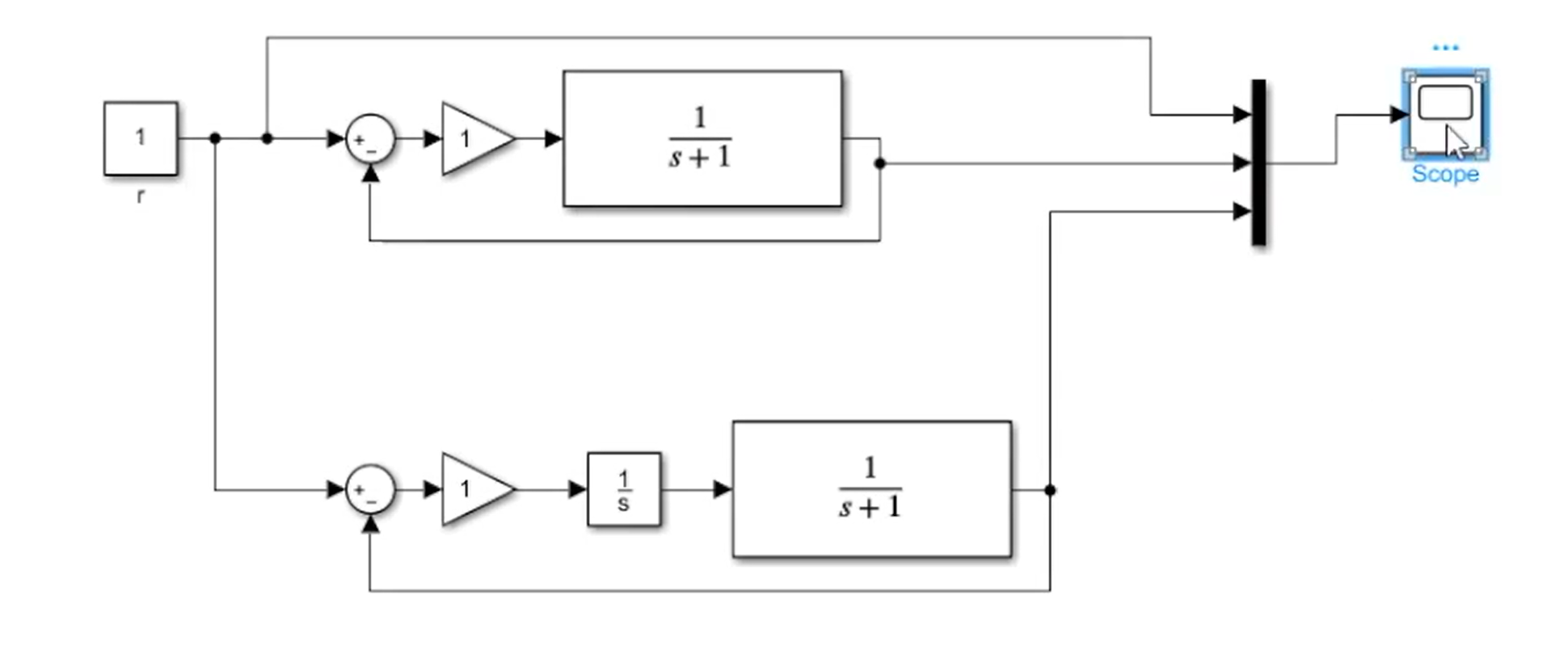
阶跃响应结果如下：

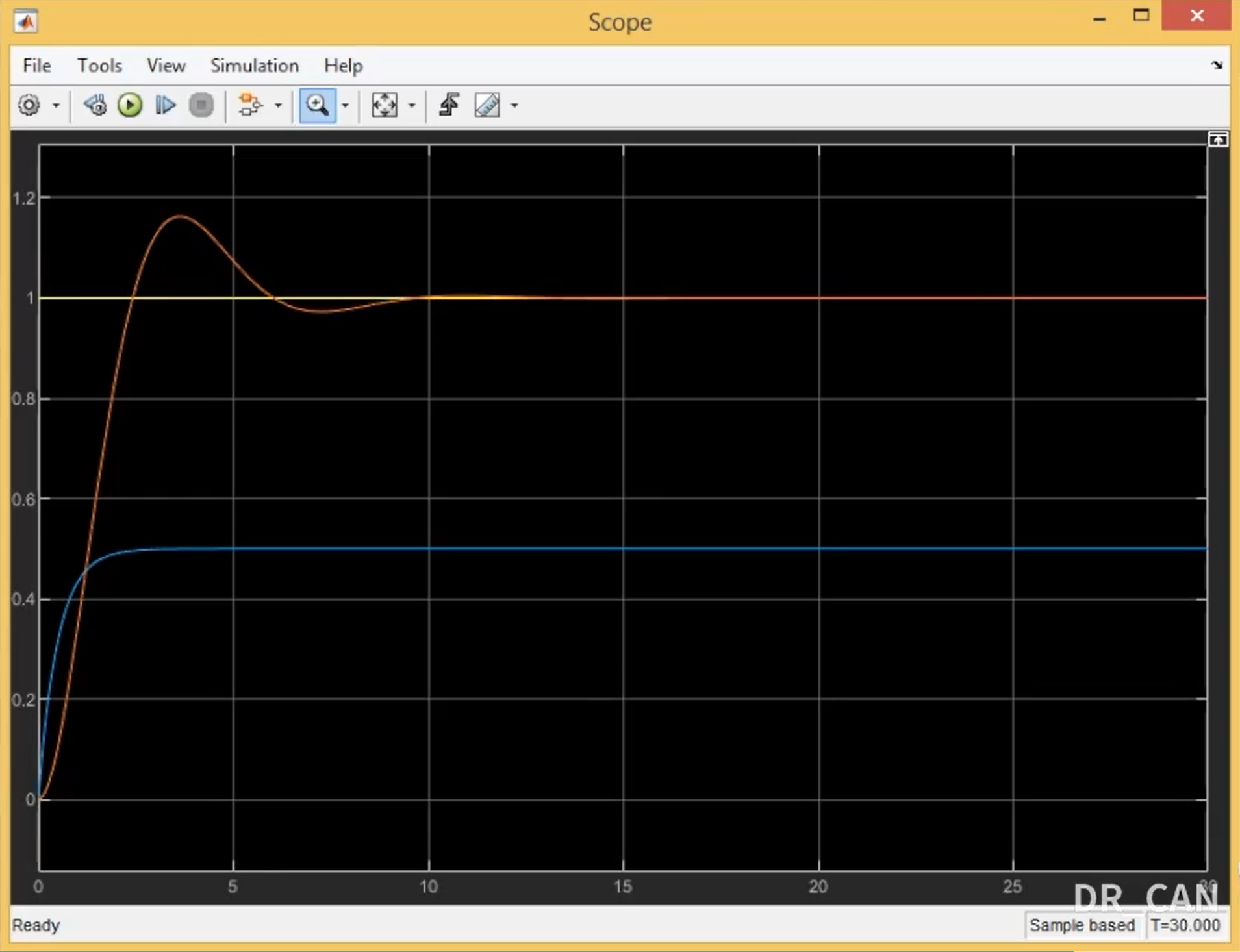
可以看到，蓝色的比例控制收敛较快，但存在较大的稳态误差，根据终值定理我们知道这个稳态误差是目标值的50%。而橙色的积分控制可以很好的消除稳态误差，但存在一定的超调和振荡，这是因为加入比例控制后给一阶系统进入了一个新的极点，具有二阶系统的阶跃响应特性。另外的，积分控制的收敛速度相对较慢，这是因为积分的过程需要一定的时间，在一开始积分较小并不能很好的驱动系统。那么我们可以通过将比例控制与积分控制结合在一起来：

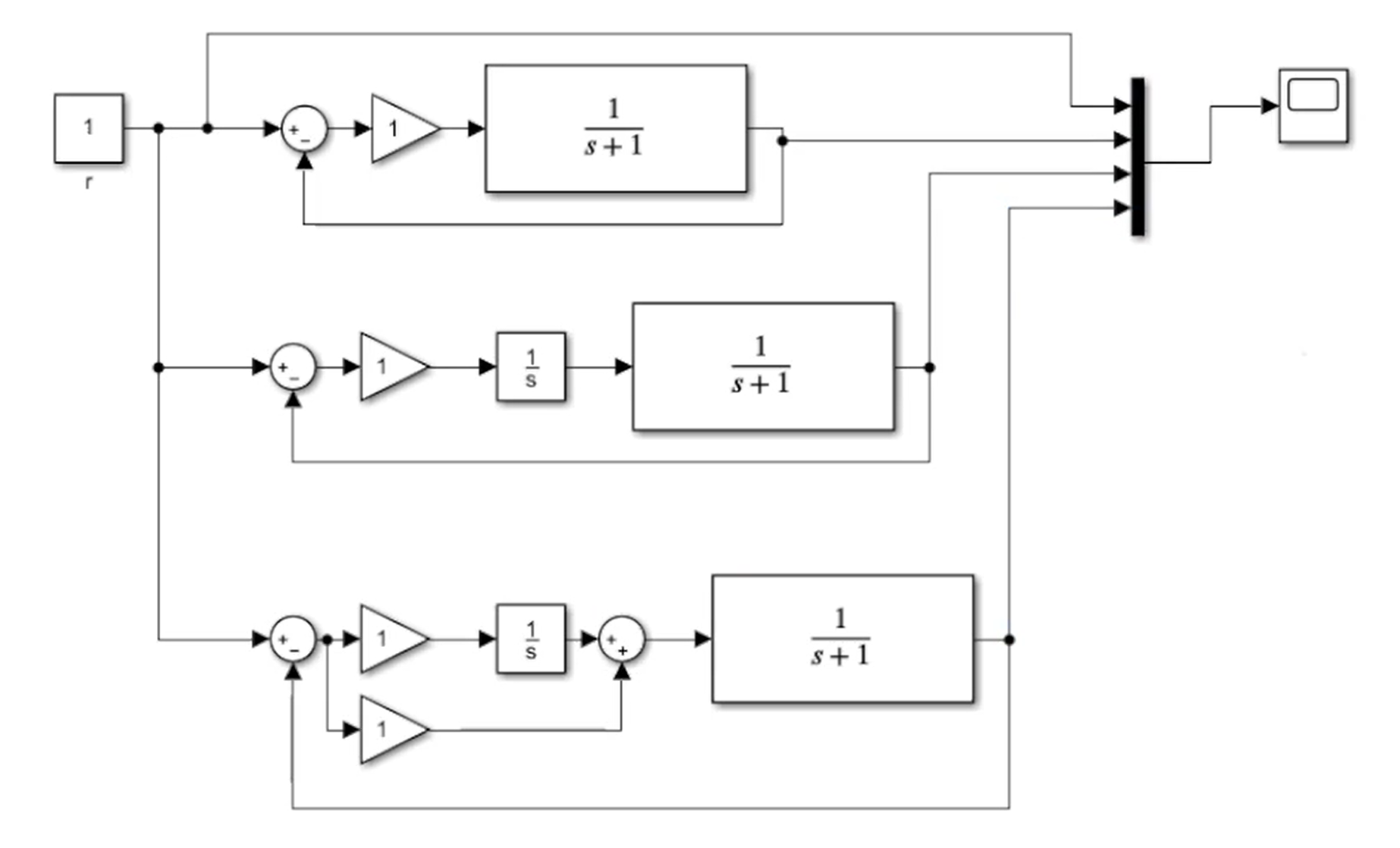
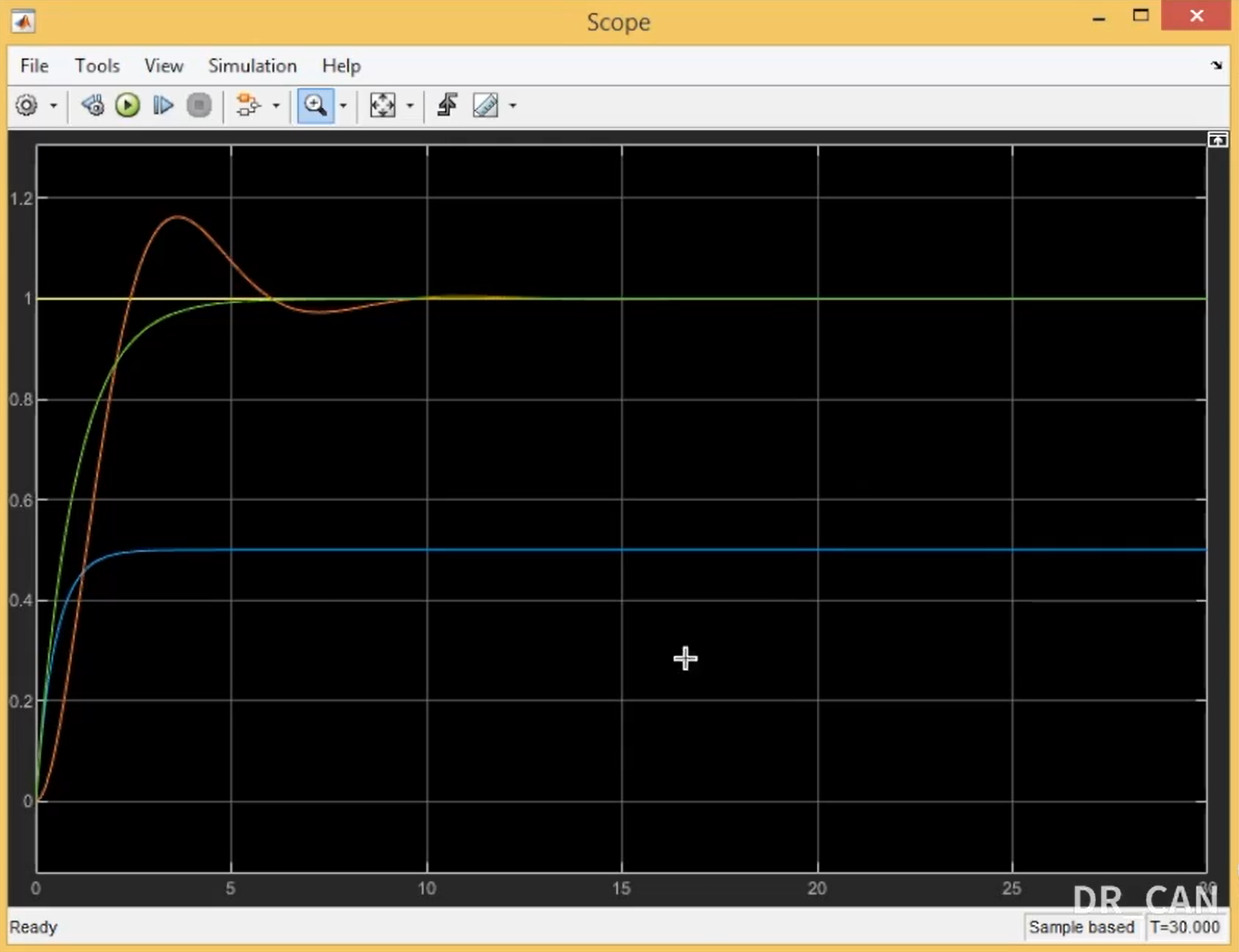
可以看到，我们新设计的比例积分控制器可以兼顾两种控制器的优点，达到收敛迅速同时可以消除稳态误差的目的。

（五）比例积分控制器

原文：https://www.cnblogs.com/HongxiWong/p/12891190.html