题目大意:
一个01串 给定每位为1的概率p 一个字符串的权值是所有连续的1的数量的平方和(e.g.110011101有3段连续的1,长度分别为2,3,1,权值2^2+3^2+1^2=14)
n<=2e5
题目解法:
很容易发现在某一位放1的贡献是 前面连续1的个数*2+1。
自己在做的时候想的是很朴素的做法。取f[i][j]表示前i位以j个1结尾(以0结尾是j=0)的概率。答案即为所有f[i][j]*(2j-1)的和。然后观察式子和转移方程我们可以把第二维消掉,直接做成前缀和。写起来很容易但是想起来真的很麻烦因为这不是一个好的方法。
正解是这样的。我们考虑按位算期望值相加。根据我们前面发现的规律,我们需要知道每位前面连续的1的个数的期望值。用dp[i]表示。显然dp[i]=(dp[i-1]+1)*p[i]。答案为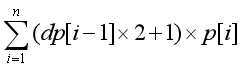
*一些思考:概率dp的转移要注意dp[i]=dp[j1]*p1+...+dp[jn]*pn, 一定要保证p1+...+pn=1。自己做的时候一开始直接将f[i][j]作为前i为以j个1结尾的期望答案,从前往后转移结果发现不对。但做完以后觉得如果从后往前转移就有可能是对的(但这样意义就不太对了边界就不会处理了……)?因为,如果我们考虑概率*贡献的朴素求和,显然一个贡献前面乘的概率是由它前面的部分得来的,与其后面的所有概率无关。所以显然应该从后往前算。就如同我们算一个dag从起点到终点的期望路径长度最后的答案是dp[s]。
*一些疑问:一开始很困惑答案为什么不是(dp[i]*2-1)*p[i](因为第i位为1的贡献也可以看作i和i前面的1的个数*2-1)。需要注意再考虑每个点的贡献是我们应该想的是如果该位放1,它的贡献是左边连续的1*2+1;如果该为为0,不做贡献。所以我们要用的是dp[i-1]。因为放0不做贡献我们显然只考虑第i为放1的情况后再乘上概率。在这种情况下第i位在连续的1中的期望序号显然是dp[i-1]+1,而非考虑到第i位放0的可能后算出来的dp[i]。
原文:https://www.cnblogs.com/myrcella/p/12892259.html