数据结构随笔——二叉树基础

一、基本概念

二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点之后，每个顶点定义了唯一的父结点，和最多2个子结点。

• 树的结点（node）：包含一个数据元素及若干指向子树的分支；
• 孩子结点（child node）：结点的子树的根称为该结点的孩子；
• 双亲结点：B 结点是A 结点的孩子，则A结点是B 结点的双亲；
• 兄弟结点：同一双亲的孩子结点； 堂兄结点：同一层上结点；
• 祖先结点: 从根到该结点的所经分支上的所有结点
• 子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙
• 结点层：根结点的层定义为1；根的孩子为第二层结点，依此类推；

性质：
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i≥1)。
性质2:深度为k的二叉树至多有2^k-1个结点(k≥1)。
性质3:对任何一棵二叉树T,如果其终端结点数为n1，度为2的结点数为n2，n1=n2+1。
性质4:具有n个结点的完全二叉树的深度为[log2n]+1 ([x]表示不大于x的最大整数)。

二、二叉树的结构和操作

存储结构：

typedef int datatype;
typedef struct BiTNode 
{
	datatype data;
	struct BiTNode *lchild, *rchild;//左右孩子指针
}node,*tree;

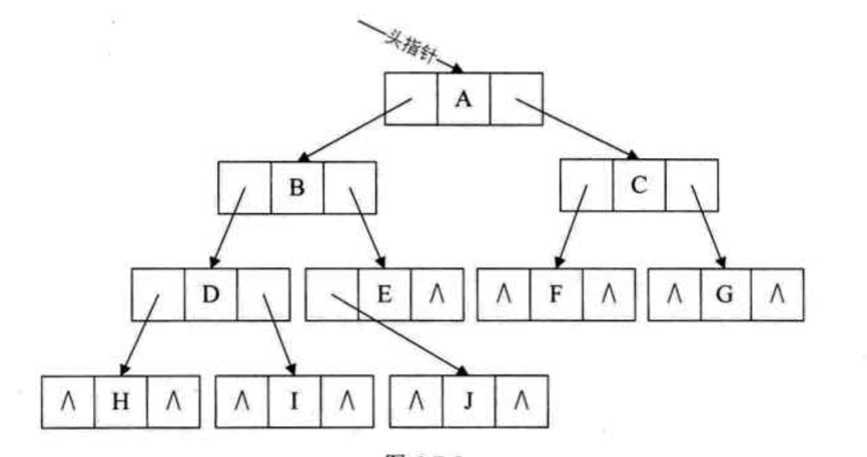
遍历二叉树

• 前序遍历

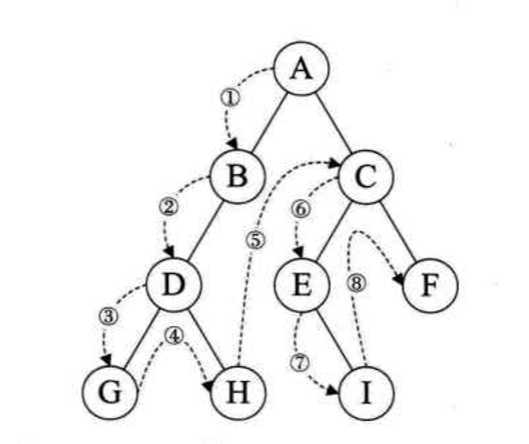
规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

void preordertraverse(tree t) //前序遍历算法
{
	if (t == NULL)
		return;
    cout << t->data <<endl; //可以插入其他操作
	preordertraverse(t->lchild);
	preordertraverse(t->rchild);
}

• 中序遍历

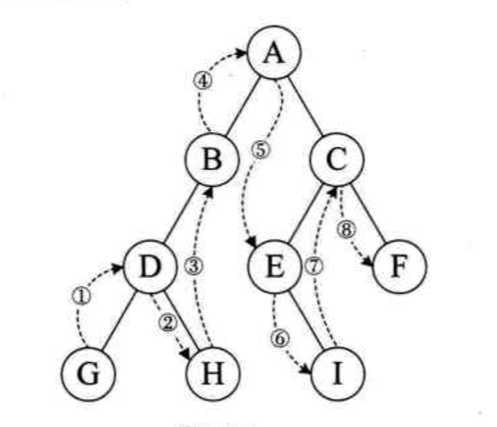
规则是若树为空，则空操作返回，否则从根结点开始(注意并不是先访问根结点)，中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

void inordertraverse(tree t)
{
	if (t == NULL)
		return;
	inordertraverse(t->lchild); //中序遍历左子树
	 cout << t->data <<  endl;
	inordertraverse(t->rchild);//中序遍历右子树
}

• 后续遍历

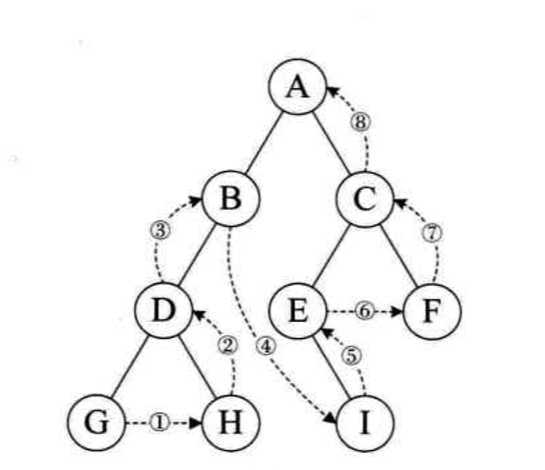
规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。

void postordertraverse(tree t)
{
	if (t == NULL)
		return;
	postordertraverse(t->lchild); //后序遍历左子树
	postordertraverse(t->rchild);//后序遍历右子树
	 cout << t->data << endl;
}

层序遍历

就是按照二叉树的层次来输出

int print_at_level(tree t, int level)
{
	if (!t || level < 0)
		return 0;
	if (level == 0) {
		cout << t->data;
		return 1;
	}
	return print_at_level(t->lchild, level - 1) + print_at_level(t->rchild, level - 1);
}

int main() {
	tree t_;
	t_ = NULL;
	createbitree(&t_);//前序创建二叉树
	for (int i = 0;; i++)
	{
		if (!print_at_level(t_, i))
			break;
	}
}

在这里经常会遇到考试问题，已知二叉树的前/后序遍历和中序遍历，如何得到二叉树？

1. 对于前序遍历，第一个肯定是根节点；
2. 对于后序遍历，最后一个肯定是根节点；
3. 利用前序或后序遍历，确定根节点，在中序遍历中，根节点的两边就可以分出左子树和右子树；
4. 对左子树和右子树分别做前面3点的分析和拆分，相当于做递归，我们就可以重建出完整的二叉树；

利用前序遍历创建

void createbitree(tree *t)//利用前序来创建一个树,t为二级指针变量
{
	datatype a;
	cin >> a;
	if (a == ‘#‘)
		*t = NULL;
	else
	{
		*t= (tree)malloc(sizeof(node));
		if (!*t)
			return;
		(*t)->data = a;
		createbitree(&(*t)->lchild);//构造左树
		createbitree(&(*t)->rchild);//构造右树
	}
}

中序，后续遍历生成二叉树只需改变递归顺序即可。

三、线索二叉树（简单了解即可）

考虑到二叉链表中的2n个指针域中有n+1个空指针域,为充分利用空间，可以用这些空指针域来保存前驱和后继指针信息。指向该线性序列中的“前驱”或"后继”的指针,称作“线索”(以区别二叉链表中的指向孩子结点的指针,利用二叉链表中的空指针做线索)。

对线索中节点的约定

增加两个标志值：

• LTag：0，Ichild域指示结点的左孩子；1，Ichild域指示结点的某种遍历的前驱；
• RTag：0，rchild域指示结点的右孩子；1，rchild域指示结点的某种遍历的后继；

结构定义

typedef char datatype;
typedef enum PointerTag {Link,Thread}PointerTag;
////枚举，Link为0，Thread为1
typedef struct BiThrNode
{
	datatype data;
	struct BiTNode* lchild, * rchild;
	PointerTag LTag;
	PointerTag RTag;
};

中序遍历线索化

void inthreading(BiThrTree p)
{
	if (p)
	{
		inthreading(p->lchild);
		if (!p->lchild)
		{
			p->LTag = Thread;
			p->lchild = pre;//左儿子指针指向前驱
		}
		if (!pre->rchild)//前驱没有右儿子
		{
			pre->RTag = Thread;
			pre->rchild = p; //前驱右儿子指针指向后继（当前节点p）
		}
		pre = p;
		inthreading(p->rchild);
	}
}

四、树，森林与二叉树的转换

树转换为二叉树

1. 加线。在所有兄弟结点之间加一条连线。
2. 去线。对树中每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线。
3. 层次调整。以树的根结点为轴心，将整棵树顺时针旋转一定的角度， 使之结构层次分明。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子。

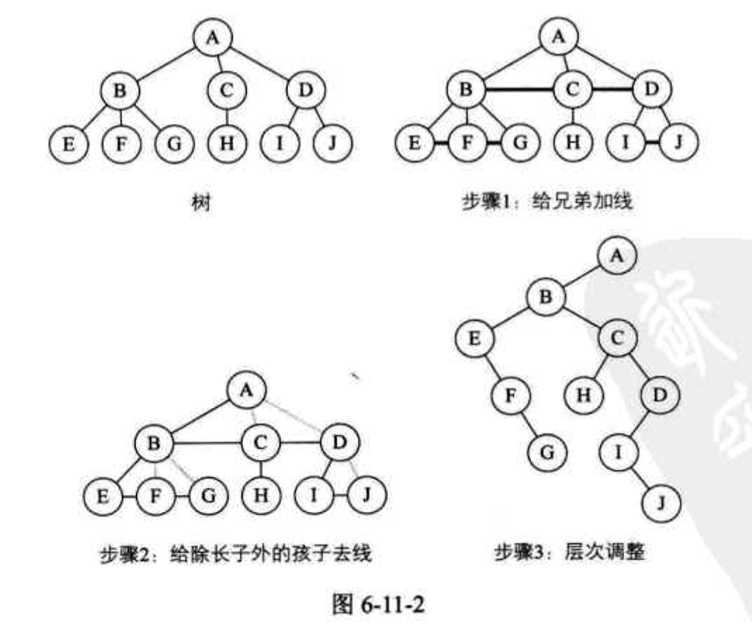
森林转换为二叉树

森林是由若干棵树组成的，所以完全可以理解为，森林中的每一棵树都是兄弟，可以按照兄弟的处理办法来操作。步骤如下:

1. 把每个树转换为二叉树。
2. 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二又树的根结点的右孩子，用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。

五、赫夫曼树

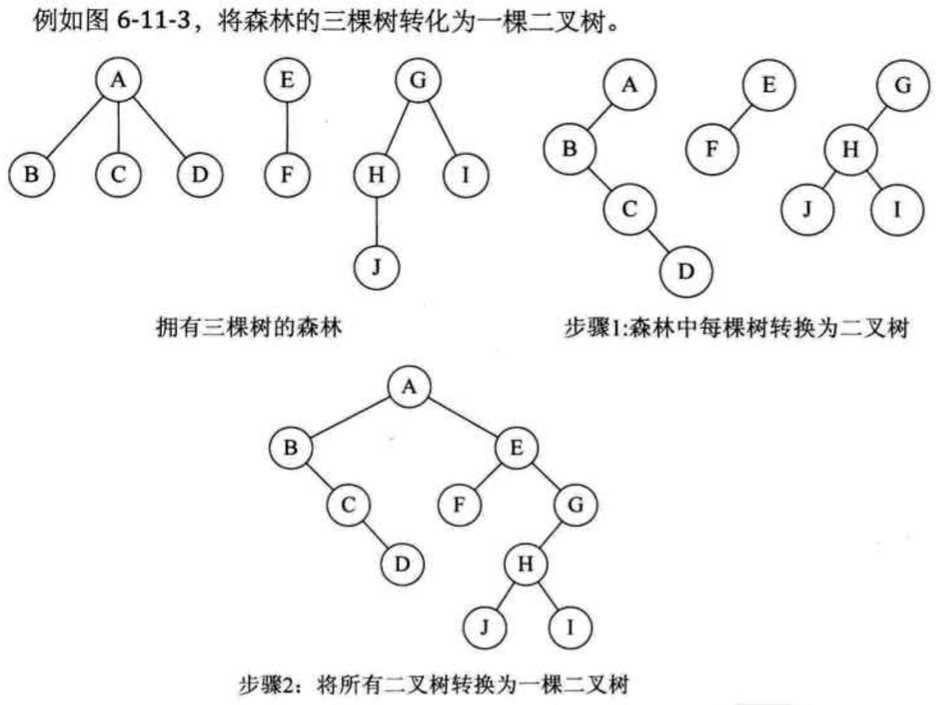
基本术语：

• 路径和路径长度

在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

• 结点的权及带权路径长度

若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为，从根结点到该结点之间的路径长度与该结点的权的乘积。

• 树的带权路径长度

树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

定义 ：

赫夫曼树( Huffman树)一又称最优二叉树,它是n个带权叶子结点构成的所有二叉树中,带权路径长度WPL最小的二叉树。

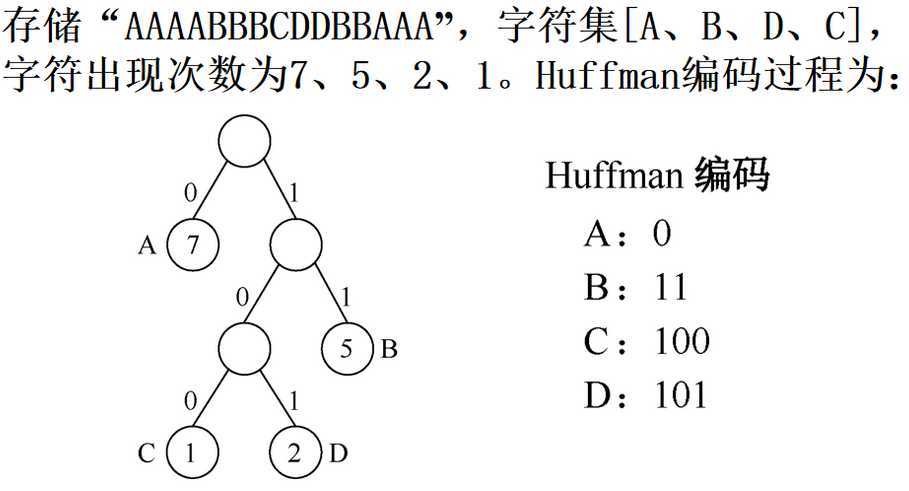
赫夫曼编码：

一般地，设需要编码的字符集为{ d1,d2,....,dn },各个字符在电文中出现的次数或频率集合为{ W1,W2,....,Wn},以d1,d2,...,dn作为叶子结点，以W1....Wn作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是赫夫曼编码。

数据结构随笔——二叉树基础

原文：https://www.cnblogs.com/lonely-ok/p/12712510.html