数据结构-图

1、图总结思维导图：

2、重要概念的笔记：

(i)Dijkstra算法:

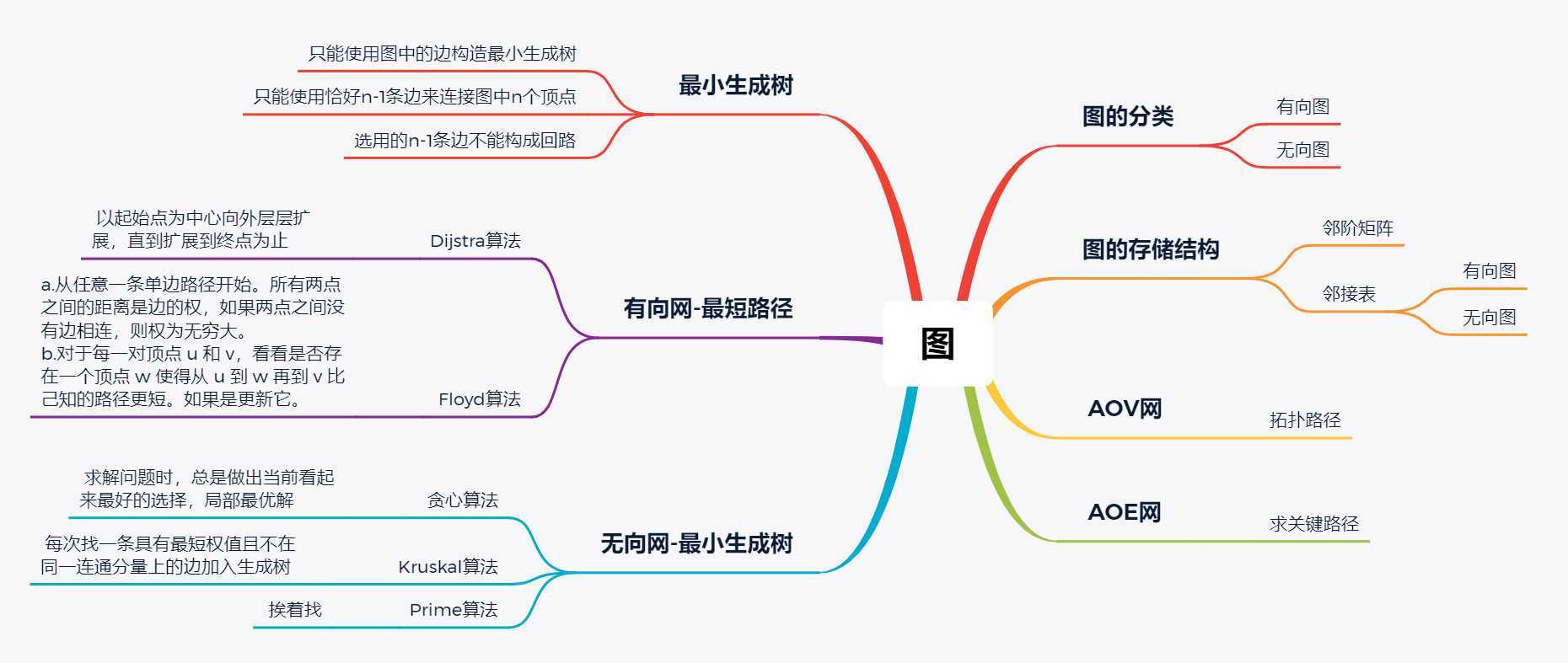
a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。
c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。

例：

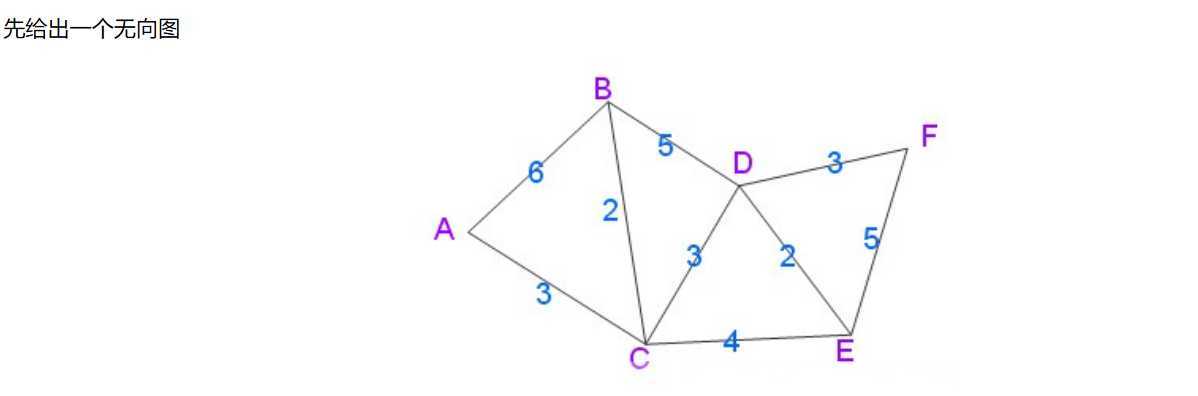
用Dijkstra算法找出以A为起点的单源最短路径步骤如下：

(ii)Floyd算法:

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　
b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

(iii)Kruskal算法:

算法实现：
<1>　设一个有n个顶点的连通网络为G（V,E），最初先构造一个只有n个顶点，没有边的非连通图T={V,空}，图中每个顶点自成一格连通分量。
<2>　在Ｅ中选择一条具有最小权植的边时，若该边的两个顶点落在不同的连通分量上，则将此边加入到Ｔ中；否则，即这条边的两个顶点落到同一连通分量 上，则将此边舍去（此后永不选用这条边），重新选择一条权植最小的边。
<3>　如此重复下去，直到所有顶点在同一连通分量上为止。

伪代码：

// 把所有边排序，记第i小的边为e[i](1 <= i <= m)m为边的个数
// 初始化MST为空
// 初始化连通分量，使每个点各自成为一个独立的连通分量

 for (int i = 0; i < m; i++){
	 if (e[i].u和e[i].v不在同一连通分量) {
		         // 把边e[i]加入ＭＳＴ
			        // 合并e[i].u和e[i].v所在的连通分量 
			    }
 }

(IV)prim算法:

算法步骤：

        选用的任意一个顶点V0,从V0开始生成最小生成树：

        <1> 初始化dist[v0]=0,其他点的距离值dist[i]=正无穷；其中dist [ i ] 表示集合VB中的点到VA中的点的距离值，

        <2> 经过N次如下步骤操作，最后得到一个含N个顶点，N-1条边的最小生成树:

               <3> 选择一个未标记的点K，并且dist [ k ] 的值是最小的；

               <4> 标记点K进入集合VA;

               <4> 以K为中间点，修改未标记点 j ,即VB中的点到VA的距离值；

        <5>得到最有生成树T。

3、疑难问题及解决方案：

问题：拓扑排序

解决：重新看老师的录频，在网上找些例子来熟悉。
正常步骤为：
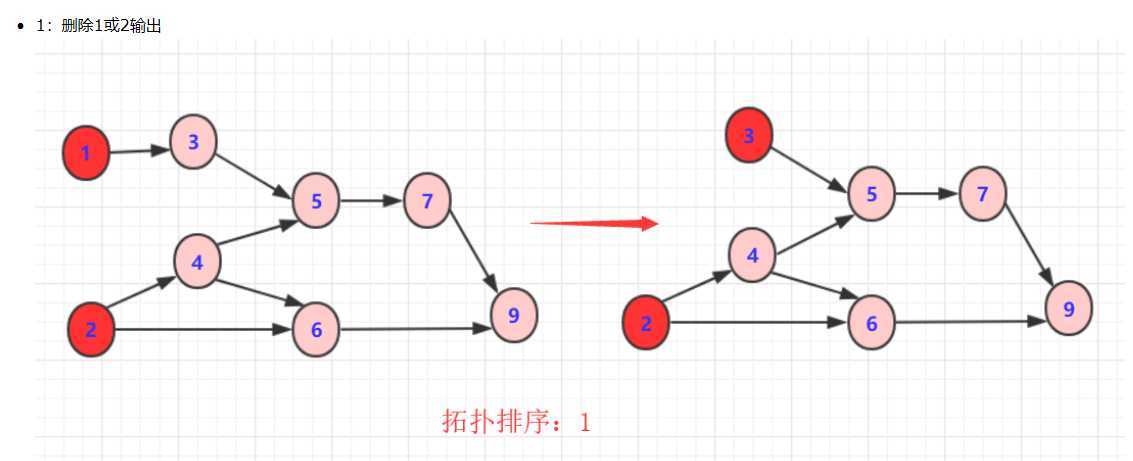
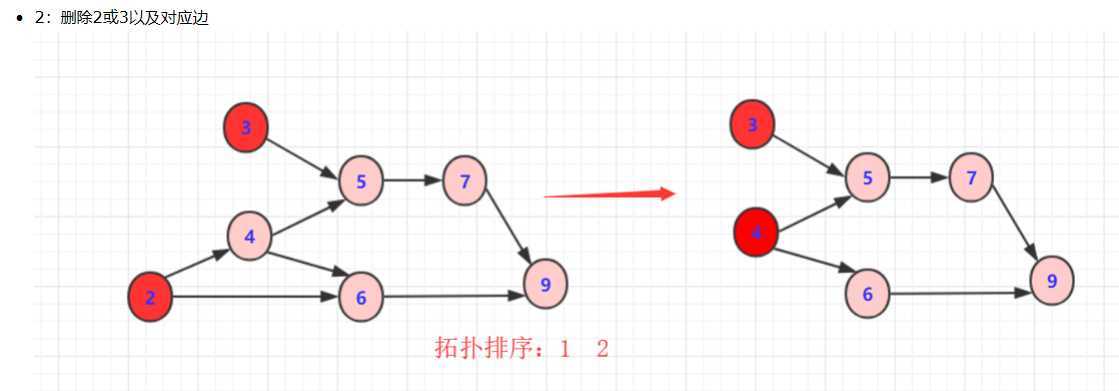
从DGA图中找到一个没有前驱的顶点输出。(可以遍历，也可以用优先队列维护)
删除以这个点为起点的边。(它的指向的边删除，为了找到下个没有前驱的顶点)
重复上述，直到最后一个顶点被输出。如果还有顶点未被输出，则说明有环！

例：

数据结构-图

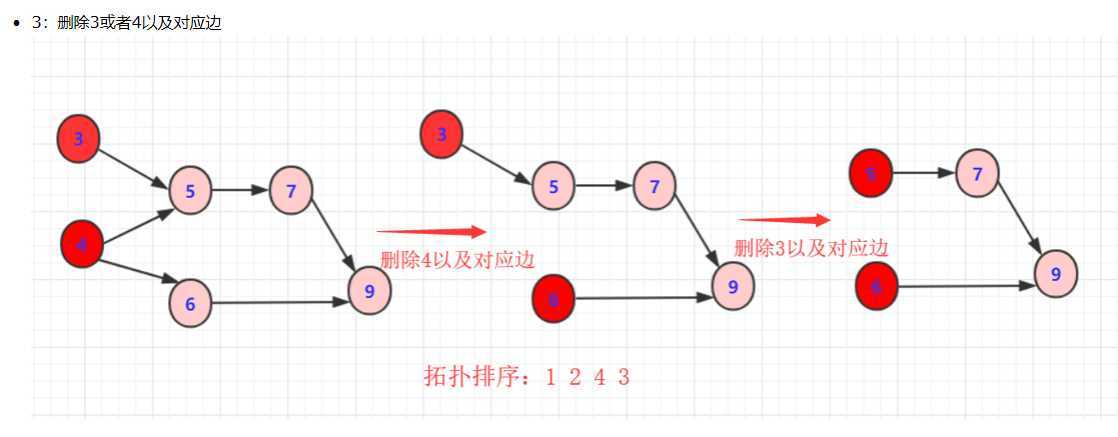
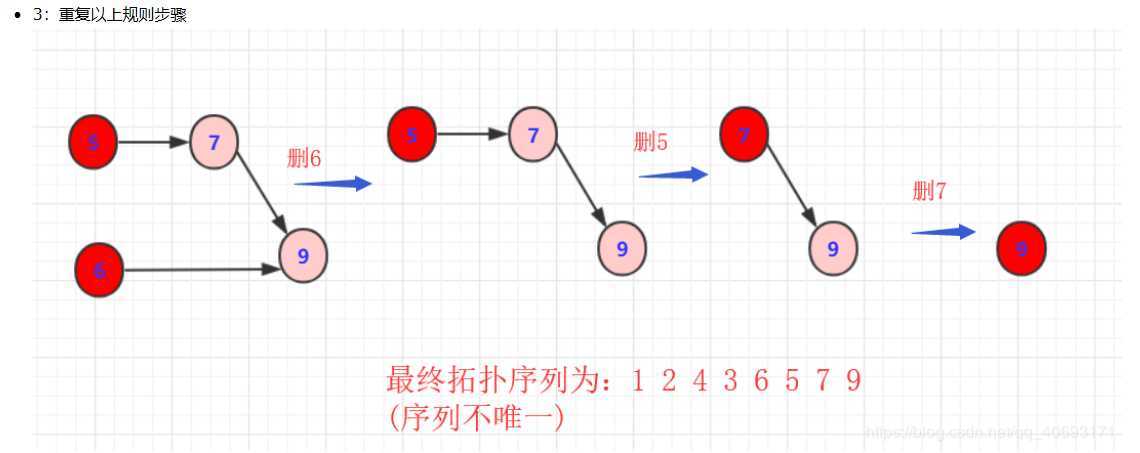
原文：https://www.cnblogs.com/fzhyxc520/p/12904713.html