Controlling bias and inflation in epigenome- and transcriptome-wide association studies using the empirical null distribution
使用经验空分布控制表观基因组和转录组范围的关联研究中的偏见和膨胀
我们显示,表观基因组和转录组范围的关联研究(EWAS和TWAS)容易导致显着的通货膨胀和测试统计数据的偏差,如果不加以解决,这种无法识别的现象会引入虚假的发现。 基于GWAS的方法和最新的混杂调整方法都无法完全消除偏差和通货膨胀。 基于经验零分布的估计,我们提出了一种贝叶斯方法来控制EWAS和TWAS中的偏差和膨胀。 使用仿真和真实数据,我们证明了我们的方法在适当控制误报率的同时最大化了功率。 我们说明了我们的方法在年龄和吸烟的大规模EWAS和TWAS荟萃分析中的实用性。
经验分布
经典统计推断主要的思想就是用样本来推断总体的状态,因为总体是未知的,我们只能通过多次试验的样本(即实际值)来推断总体。经验分布函数是在这一思想下的一种方法,通过样本分布函数来估计总体的分布函数。
引自:https://blog.csdn.net/tian_panda/article/details/80742801
null distribution
假设检验时,原假设null hypothesis 成立时的分布就是null distribution
人口研究中表观基因组和转录组数据的大规模分析被认为回答了有关基因组生物学的基本问题,并将有助于将遗传和环境影响与疾病病因联系起来[1、2]。在全球范围内,研究小组正在联合起来生成和分析此类数据[3-7],以补充已经可用并已成功用于全基因组关联研究(GWAS)的大量遗传数据资源。尽管用于GWAS的分析工具箱已经成熟,但是用于分析表观基因组和转录组范围的关联研究(EWAS和TWAS)的有效方法的开发是一个新兴的研究领域。在EWAS中,通常测试通常成千上万个CpG二核苷酸的DNA甲基化水平与目标结果的关联,而在TWAS中,要对成千上万个基因的表达水平进行测试。当前,EWAS和TWAS分析在很大程度上依赖于专为GWAS设计的方法。但是,表观基因组和转录组数据与遗传数据至关重要。它们是定量方法(并非像基因型那样离散),受技术批次和生物学影响(包括细胞异质性)的主要混杂影响[2,8]。此外,与基因型标记相比,诸如DNA甲基化和基因表达等分子表型通常表现出与表型性状或复杂疾病的更强关联。
全美范围关联研究分析的一个关键方面是对检验统计膨胀的控制。测试统计数据的膨胀会导致对统计显着性水平的高估,并大大增加假阳性结果的数量[9]。这一直是GWAS中的主要关注点,但是在EWAS中也观察到过高的测试统计数据[10,11]。通货膨胀水平经常超过GWAS中观察到的水平,但通常不予纠正[12]。在GWAS中,通常使用基因组控制来解决测试统计膨胀问题,其中将膨胀的测试统计数据除以基因组膨胀因子。基因组通货膨胀因子通过比较观察到的所有基因变异的测试统计数据与无效果假设下的预期通货膨胀估计通货膨胀量[9]。最近的工作指出了GWAS中基因组控制的关键局限性[13,14]。值得注意的是,当感兴趣的结果与许多小的遗传效应相关时,基因组膨胀因子被证明不能提供检验统计膨胀的无效估计[13]。在EWAS和TWAS中,这是规则而不是例外。此外,检验统计数据不仅可能受到膨胀的影响,还会受到偏差的影响[15],使用基因组控制时无法对其进行校正。检验统计的偏差会导致效应大小分布的变化,并由混淆[16,17]驱动,这是EWAS和TWAS的突出特征,但在GWAS中却很少受到关注[18]。因此,这需要开发专门设计用于解决EWAS和TWAS分析中检验统计膨胀和偏差的新方法。
尽管通常被忽略,但是基因组控制将高估实际的通货膨胀率,除非根据不与目标结果相关的遗传变异进行估计[9,19]。提出了贝叶斯离群模型[20]来解决这个问题。它估计通货膨胀率,同时假设10个相关的遗传变异数量固定且数量很少。尽管这对于具有较少关联的GWAS而言是一种改进,但不足以解决EWAS和TWAS中通货膨胀率过高的估计,而通货膨胀通常会大大增加关联。它也没有解决测试统计偏差的发生。在统计文献中,已在大规模多重假设检验的背景下提出了替代方法,其中使用经验空值分布进行推断[16,21–23]。但是,这些方法在EWAS和TWAS中的效用仍有待评估。在这里,我们使用模拟研究以及大规模的甲基化组(n = 2203)和转录组(n = 1910)数据[24、25]来表明,通过应用基因组控制来校正膨胀的测试统计数据对于EWAS和TWAS来说过于保守统计偏差不能忽略。此外,我们证明了检验统计偏差和通货膨胀由经验零分布的均值和标准差表示,并提出了一种贝叶斯方法进行估计。包括SVA [26],RUV [27]和CATE [17]在内的最新批次校正方法的应用无法消除所有测试统计偏差和膨胀。因此,所得到的测试统计数据需要进行经验校准,以实现最佳的统计功效,同时将误报的数量控制在所需水平。我们开发了一种用于估计经验空值分布的贝叶斯方法,并提出了作为R / Bioconductor [28,29]程序包BACON实施的偏差和通货膨胀校正。最后,我们通过对两个普遍研究的结果进行年龄,吸烟状况的EWAS和TWAS荟萃分析,证明了我们方法的实用性。
Results
The genomic inflation factor is not suitable to measure inflation in EWAS/TWAS
研究使用来自两个人群(LLS和LL)共500个受试者的基因组甲基化数据和转录组数据,对年龄和吸烟状况进行EWAS和TWAS分析(线性模型,血细胞信息作为协变量)。
使用常用的genomic inflation factor对分析结果的膨胀性进行衡量,EWAS为1.33至1.72,TWAS为1.21至1.54(见下图)
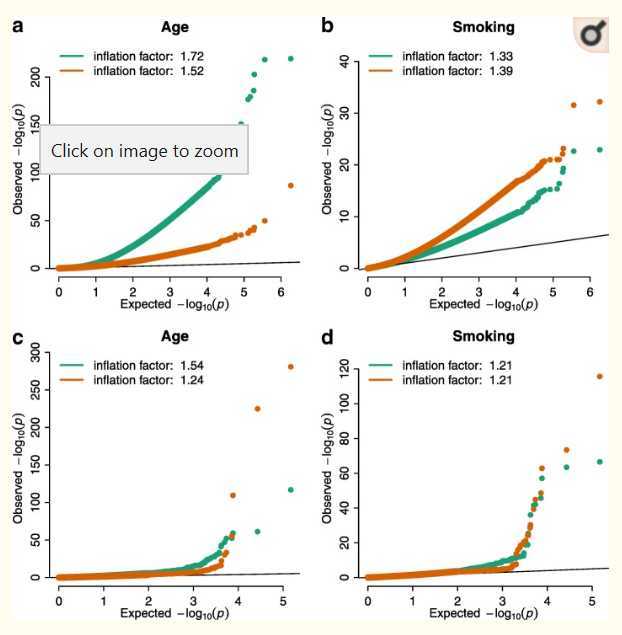
注:图a,b为EWAS分析的结果,图c,d为TWAS的分析结果。绿色线为LL人群的分析结果,橘色线为LLS的分析结果。
然而,genogenomic inflation factormic inflation factor与expected number of true associations有关。例如,年龄的膨胀系数比吸烟的膨胀系数高,已有研究表明,与吸烟相比,年龄与更多的甲基化位点、表达基因差异有关(基因多效性)。再如,LL的基因组膨胀因子高于LLS,这可能是因为LL(21岁年龄段)比LLS(9岁年龄段)具有更高的统计功效(statistical power)。
通过模拟研究发现,实验组的true associations越高,genomic inflation factor越高。该结果也可以由数学方法推导得到。
所以我们认为genomic inflation factor会高估EWAS和TWAS中test-statistic膨胀的真实水平。
test statistic: Sample used to determine whether a hypothesis will be accepted or rejected. If the test statistic is too far off of the original hypothesis, it will be rejected. Conversely, when a test statistic is close to the original hypothesis, it will likely be accepted.
用于确定假设是被接受还是被拒绝的样本。 如果检验统计量与原始假设相距太远,它将被拒绝。 相反,当检验统计量接近原始假设时,它可能会被接受。
EWAS/TWAS not only suffer from inflation but also from test-statistic bias
除了用qq图来作为分析结果膨胀性的可视化方法,还可以用绘制统计量的直方图来观察膨胀性,即test statistical bias。该偏差可以看作是观察到的测试统计量的众数与零(即标准正态分布的众数)之间的偏差。由于假定大多数表型(遗传变异,CpG或基因)与目标结果无关,因此从线性模型获得的检验统计数据应遵循标准正态分布(即以零为中心)。
我们观察到年龄和吸烟的EWAS和TWAS中的检验统计偏差。genomic control不能解决bias,因为它使用模式固定为零的正态分布(附加文件2)。图中说明了通过基因组控制观察到的测试统计分布的错误。请注意,即使是基于置换(permutation)的方法(通常被认为是为了挽救违反有关理论零分布的假设的方法)也不会得到较好的零分布,并且检验统计偏差和膨胀都将持续存在。我们通过数学推论得出,未观察到的混杂因素在高维数据分析(附加文件2)中引入了偏差。
转录组范围关联研究中的偏差。 生命线(LL)队列中来自年龄TWAS的测试统计数据的直方图。 每个图显示不同的零分布,为了进行比较,每个面板中都显示了理论上的空值(绿色)。
a理论零假设(theoretical null,绿色):均值和方差为(0.0,1.02)的正态分布,
b经验零假设(empirical null, 褐色):使用我们的贝叶斯方法(0.23,1.52)估计均值和方差的正态分布,
c夸大零假设(inflated null, 紫色): 均值和方差为零的正态分布等于使用基因组控制方法估算的估计通货膨胀率(0.0,1.52),
d置换零假设(permutation null, 粉红色):具有基于均值和方差的基于置换的估计值的正态分布(-0.006,1.12)。
Estimating test-statistic bias and inflation
bias和inflation都表示与理论零分布的偏差:bias(如平均值)、a deviation from zero(如标准差)和inflation。因此,估计bias和inflation的大小与估计经验零分布的参数的方法应该是一样的。本文开发了一种贝叶斯方法,可以从一组数据中估计经验分布,并获得bias和inflation的估计值。该方法使用Gibbs sampling算法将3-component normal mixture拟合到观察到的数据集中。一个分量(component)代表了零分布及其平均值和标准差(代表bias和inflation)。带有正负平均值的其它两个component代表在数据中观察到的true association的数量。因此,该方法在不受未知比例的true association的影响下,同时提供bias和inflation的估计值。
作者在模拟研究中,对该方法和genomic方法估算了经验分布,结果表明该方法优于genomic方法。此外,该方法得出的inflation factor最稳定,表明其它方法存在随机高估或低估了膨胀系数的现象。
在两个队列(LifeLines和Leiden Longevity Study)中进行的TWAS的年龄(a和b)和吸烟状况(c和d)的测试统计数据直方图。 曲线表示使用我们的贝叶斯方法估算的三成分正态混合物。 黑线表示混合物的拟合,红线表示null component的拟合((the empirical null distribution with estimated mean and variance reported)。 蓝线和绿线表示alternative components的估计拟合度(proportion of positively and negatively associated features)。
最该关注那一条线?线应该是怎样表明拟合好??
Correction for unobserved covariates reduces test-statistic bias and inflation
通货膨胀和偏见的主要原因被认为是无法衡量的技术和生物学混淆[8,16],例如种群的亚结构,批次效应和细胞异质性。已经开发出各种方法来减少这些无法测量的因素对高维数据的影响[17、26、27、32-34]。我们应用了其中的六种方法来调整LLS队列的500名个体的EWAS和TWAS年龄,并研究了它们对检验统计偏倚和通货膨胀的影响。与仅使用已知协变量的模型相比,所有方法都减少了偏差和通货膨胀的量(表(表格11和其他文件1:表S2)。尽管如此,仍观察到残余偏差和通货膨胀。因此,我们设计了一种两阶段方法,以便在保留统计能力的同时适当控制误报的数量。首先,我们进行了分析,以校正已知的生物学和技术协变量以及估计的未观察到的协变量,然后使用经验零分布估算和调整残留偏差和通货膨胀。在调整步骤中,使用经验零值分布代替基因组控制方法使用的标准正态或膨胀正态来计算P值。基因组膨胀因子的一个复杂之处在于,它估计零分布的方差(λχ21个),而标准偏差(λχ21个---√基因组控制对具有连续结果的线性模型(此处为DNA甲基化和基因表达数据)产生的正态分布检验统计数据进行基因组控制是必需的。此外,重要的是要注意,偏差不仅会导致错误的测试统计数据和P值,而且还会导致效果大小的偏差估计。为了评估两阶段方法的性能,我们进行了数值模拟。为了解决无法测量的混杂问题,我们选择了CATE,这是一种最新方法,与其他方法相比,该方法在估计未观察到的协变量方面具有优越的性能[17]。我们的贝叶斯方法与CATE相结合产生了最高功效,假阳性率接近标称水平(0.058±0.0052)。相反,忽略未观察到的协变量的方法导致较高的假阳性率,而使用基因组控制的方法导致较低的功效(表(表2)。2)。同样,已建议与CATE [17]结合使用的测试统计校准是保守的,导致功耗较低,这与该方法与基因组控制密切相关的事实是一致的。
除了混淆之外,特征(即CpG和基因)之间的相关性还可能导致测试统计数据膨胀或偏差。 第二项模拟研究表明,如果测试统计数据相互关联,我们的贝叶斯方法可以在保持功率的同时正确控制误报率(表(表3)。3)。 同样,基因组控制的应用过于保守(表(表33和附加文件3)。
Fixed-effect meta-analysis with control for bias and inflation
类似于GWAS的当前实践,EWAS和TWAS领域的主要发展是对多个人群研究的组合分析,以发现越来越多的协会,包括影响规模较小的协会。固定效应荟萃分析结合了不同研究的估计效应大小及其标准误差,以构建合并的估计,从而提高了效应大小估计的准确性,因此具有更好的统计能力[35,36]。我们在四个队列中分别进行了年龄和吸烟状况的EWAS和TWAS评估,分别具有2203个人的甲基化组和1910个人的转录组数据。我们通过固定效应荟萃分析将四个队列的结果合并在一起(表(表44和附加文件1:图S5)。如前所述,使用CATE解决无法衡量的混淆后,仍然存在偏见和通胀。与使用我们的贝叶斯方法得出的估计值相比,使用基因组控制进行的通货膨胀估计值在分析和队列研究中的变量更高且显着更多(表(表4)。4)。贝叶斯方法完全消除了所有偏差和通货膨胀。至关重要的是,与使用基因组控制的荟萃分析相比,荟萃分析中的偏倚(<| 0.03 |)和通货膨胀(<1.14)保持最小(表(表4)。4)。后者与根本无法解决通货膨胀的方法或使用基因组控制的方法形成鲜明对比:在荟萃分析中,这两种方法都可能导致高水平的通货膨胀和偏见,而通货膨胀和偏见往往远高于单个队列。确定的年龄和吸烟率最高的流行品包括先前研究中一致报道的那些[3-7]。此外,在大规模荟萃分析中同时进行的EWAS和TWAS分析显示,分别针对年龄和吸烟的410和57个基因这两种研究类型的结果存在显着重叠(将最近的基因分配给CpG位点) (附加文件4-7:表S3a-d)。例如,附近的DNA甲基化以及CD248,DNMT3A和FBLN2的表达都与年龄有关(图。(图55个一个),a),吸烟的GPR15,AHRR和CLDND1也是如此(图。(图55个b)。b)。总共15967个(3.5%)CpG位点和1020个(2.7%)基因与年龄显着相关(Bonferroni校正的P值<0.05)。对于吸烟,相关的CpGs和基因的数量分别为1128(0.25%)和301(0.80%)。
原文:https://www.cnblogs.com/jialinliu/p/12910828.html