使用sklearn库初次尝试PCA和T-SNE,原理还不太理解,写错了请一定指出,或者等我自己发现hhhh
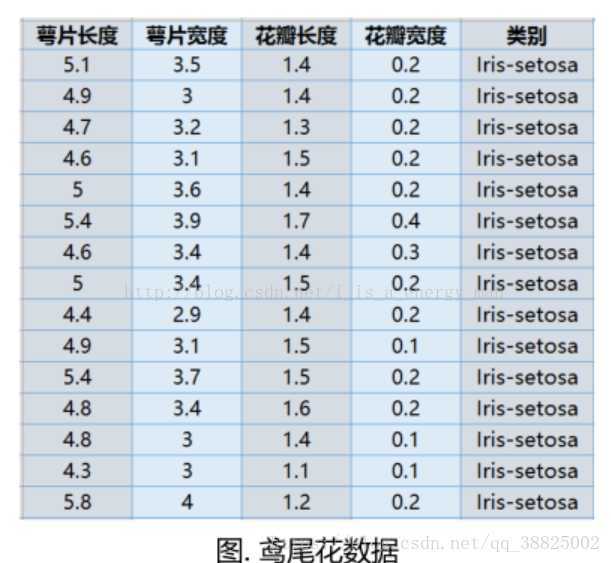
首先读入sklearn里自带的鸢尾花数据库,并调用相关的包,再查看一下这些数据都是些啥:
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
data1 = load_iris()
print type(data1)
x = data1.data
y = data1.target
print type(x)
print x.shape
结果:
data1是个对象,调用.data和.target可以查看变量的值和已经知道的鸢尾花种类分类,x和y都是数组类型,里面存放数据。
样本总数是150个,种类用012表示,有三类。
<class ‘sklearn.utils.Bunch‘>
<type ‘numpy.ndarray‘>
(150L, 4L)
(150L,)
函数原型为sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False),具体参数设置:
| 参数 | 解释 | 数据类型 |
|---|---|---|
| n_components: | PCA算法中所要保留的主成分个数n,也即保留下来的特征个数n | int 或者 string,缺省时默认为None,所有成分被保留。赋值为int,比如n_components=1,将把原始数据降到一个维度。赋值为string,比如n_components=‘mle‘,将自动选取特征个数n,使得满足所要求的方差百分比。 |
| copy | 表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进行运算;若为False,则运行PCA算法后,原始训练数据的值会改,因为是在原始数据上进行降维计算 | bool,True或者False,缺省时默认为True |
| whiten | 白化,使得每个特征具有相同的方差 | bool,缺省时默认为False |
PCA对象的方法:
| 对象名称 | 解释 | 返回值 |
|---|---|---|
| fit(X,y=None) | 表示对X数据进行训练。每个需要训练的算法都会有fit()方法,就是实现算法中“训练”的过程,y=groundtruth,PCA是无监督学习,故等于none。 | 调用fit方法的对象本身。比如y=pca.fit(X),表示用X对pca这个对象进行训练,得到的y是个PCA对象?里面仍然具有其他方法? |
| fit_transform(X) | 用X来训练PCA模型,同时返回降维后的数据。 | newX=pca.fit_transform(X),newX就是降维后的数据,array格式 |
| inverse_transform() | 将降维后的数据转换成原始数据 | X=pca.inverse_transform(newX),X是原始4维数据? |
| transform(X) | 将数据X转换成降维后的数据。当模型训练好后,对于新输入的数据,都可以用transform方法来降维。我不太明白,这个模型训练好指的是什么?投影矩阵吗?会存在哪里?还是作为一个返回值? | 降维后的数据 |
| get_covariance() | ||
| get_precision() | ||
| get_params(deep=True) | ||
| score(X,y=None) |
采用fit_transform(x)函数对x这个四维数据进行训练,并且得到返回后的二维值。注意!不要觉得x和y都写在一个表格里就是二维数据,要理解为y是由4个x1、x2、x3、x4共同确定,表示在一个四维空间里的。
pca = PCA(n_components=2) #
#print pca
# PCA(copy=True, iterated_power=‘auto‘, n_components=2, random_state=None,
# svd_solver=‘auto‘, tol=0.0, whiten=False)
reduce_X = pca.fit_transform(x)
# 查看降维后的数据分布
plt.scatter(reduce_X[:,0], reduce_X[:,1],c = y)
plt.show()
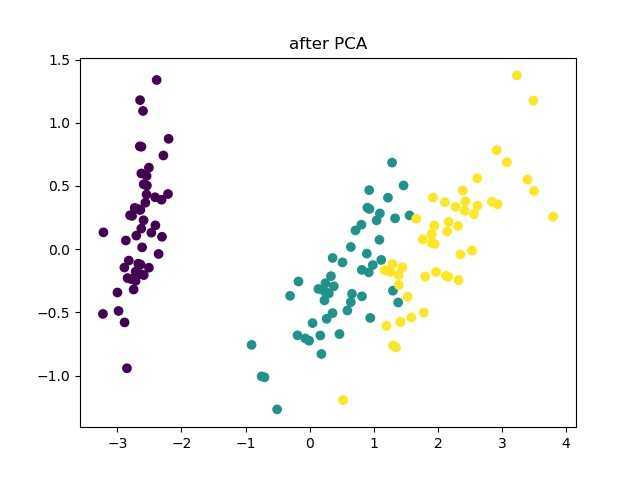
也可以分开画图,采用不同的颜色和形状表示:
for i in range(len(reduce_X)):
if y[i]==0:
rx.append(reduce_X[i, 0])
ry.append(reduce_X[i, 1])
else:
if y[i]==1:
bx.append(reduce_X[i, 0])
by.append(reduce_X[i, 1])
else:
gx.append(reduce_X[i, 0])
gy.append(reduce_X[i, 1])
plt.scatter(rx, ry, marker=‘o‘)
plt.scatter(bx, by, marker=‘D‘)
plt.scatter(gx, gy, marker=‘s‘)
plt.title(‘iris after pca‘)
plt.savefig(‘./iris_after_pca.jpg‘)
plt.show()
结果:
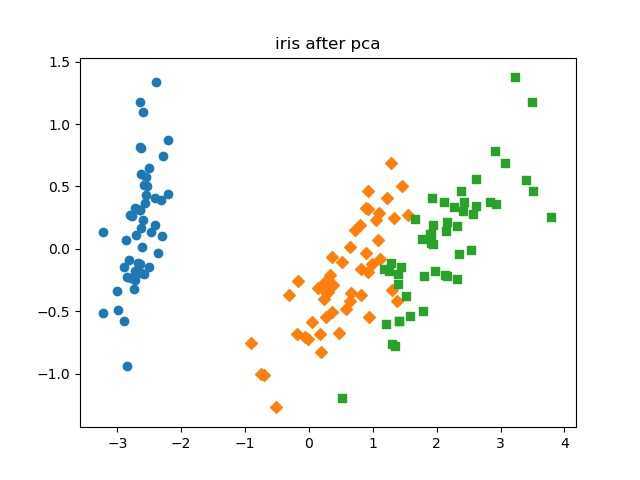
也就是说,现在这3种鸢尾花可以只用2个变量表示就可以区分
tnse = TSNE(learning_rate=100)
reduce_X = tnse.fit_transform(x)
print reduce_X.shape
很神奇,它自己降到2维了……,可视化一下
plt.scatter(reduce_X[:,0], reduce_X[:,1],c = y)
plt.title(‘iris after tnse ‘)
plt.savefig(‘./iris_after_tnse.jpg‘)
plt.show()
结果:
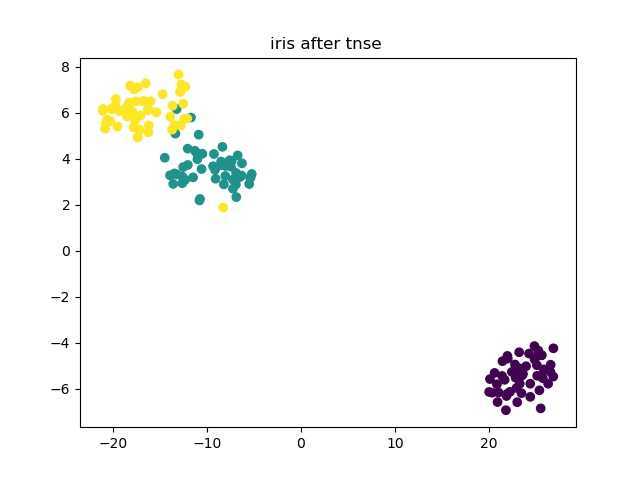
马住可能会看的文章:
关于mle的参数设置问题:
http://www.cnblogs.com/bambipai/p/7787854.html
原文:https://www.cnblogs.com/sweetsmartrange/p/12917813.html