以hidoCoder上的一道裸题为例
如果我们不会manacher算法。我们应该如何解决这个问题呢?
我们首先学习一个叫中心扩展算法的东西。
对于回文串我们可以选择一个中心,进行左右扩展,判断左右两边字符是否相等。
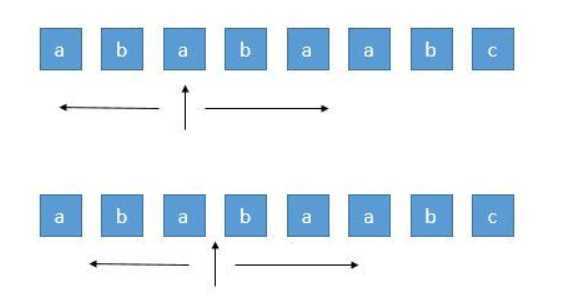
因为字符存在奇数个或者偶数个,我们可以选择每个字符或者两个字符之间的空格进行扩展。所以总共可以产生2 * n - 1个中心。
实验实现的代码:
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i); //从一个字符扩展
int len2 = expandAroundCenter(s, i, i + 1); //从两个字符之间扩展
int len = Math.max(len1, len2);
//根据 i 和 len 求得字符串的相应下标
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
private int expandAroundCenter(String s, int left, int right) {
int L = left, R = right;
while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
L--;
R++;
}
return R - L - 1;
}
空间复杂度:O(1)
时间复杂度:O(n^2)
显然时间复杂度相对于空间复杂度,更高。
我们可以考虑利用空间来换时间。
Manacher算法
我们首先用它解决奇偶数问题
我们再两个字符之间添加一个分隔符,可以插入‘#‘
转换后一定是奇数
len数组的引入
回文半径定义
len[x] - 1就是回文长度
关键在于对len数组的求解
原文:https://www.cnblogs.com/lightac/p/12719612.html