XGBoost相当于是GBDT的工程实现,其创新点有如下:
1、拟合残差利用了泰勒展开
2、加入正则项防止过拟合
3、每一轮用贪心方法分裂树,用分桶近似计算
4、每一个弱分类器都要乘以一个shrinkage(也叫step size)
5、特征抽样(列抽样)
GBDT的做法是用负梯度方向去代替残差方向。
xgboost则利用了泰勒展开,加快推到速度。
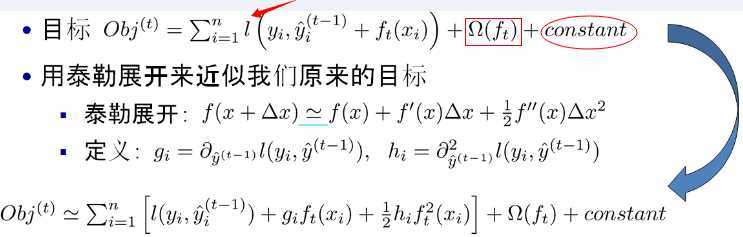
图中$\Omega$是正则项,constant是常数项。
从目标函数可以看出,每一次迭代,都在现有树的基础上,增加一棵树($f_{t}(x_{i})$)去拟合前面树的预测结果与真实值之间的残差,最终的目标函数只依赖于每个数据点在误差函数上的一阶导数和二阶导数。
在决策树的构建阶段加入了正则项:
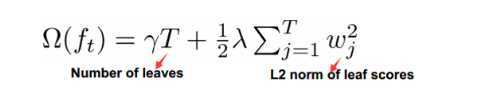
$T$是树中叶子节点的个数,约束着每一棵树不要分裂的太多,避免过拟合。
$w_{j}$是叶子节点$j$的得分(可以理解为每个样本在这棵树中的预测结果),这是一个L2正则,约束着这棵树分出来的结果不要过于激进,如果分出很大的数就会被惩罚。这样可以保证增加的每一棵树只是前进一点点,避免过拟合。
将正则项拆开并与损失函数合并到一起,得到
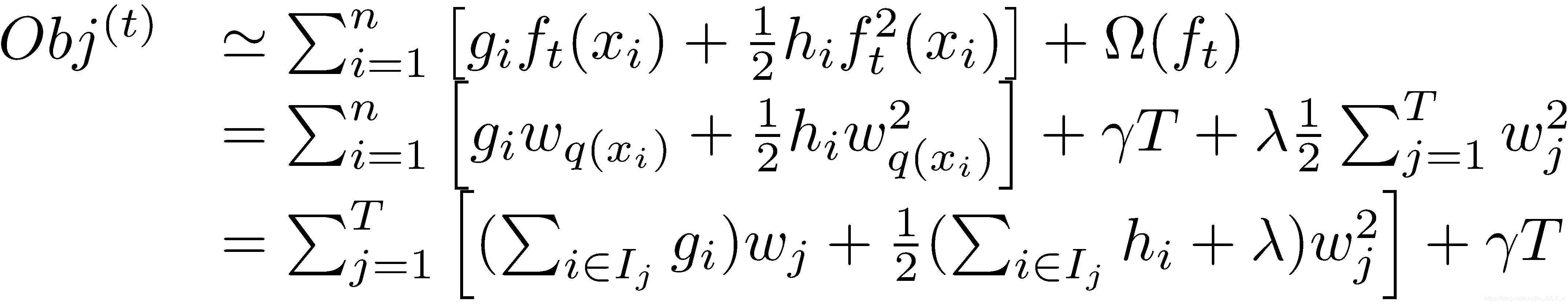
其中$I_{j}$定义为每个叶节点$j$上面样本下标的集合$I_{j}={ i|q(x_{i})=j }$,函数$q(x_{i})$是一个映射,负责控制将样本$x_{i}$映射到哪一个叶子节点
定义
![]()
则目标函数可以转化为
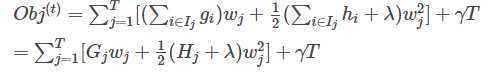
目标函数求最值,对自变量$w_{j}$求导。得到理想叶子分数
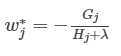
带入目标函数中,有
![]()
这个$Obj$叫做一颗树的结构分数,这个分数越小,代表这棵树的结构越好。这个分数用来评估决策树的好坏,是为了计算后面更广泛的目标函数而产生的中间过程。下面这个图可以阐释这一点。
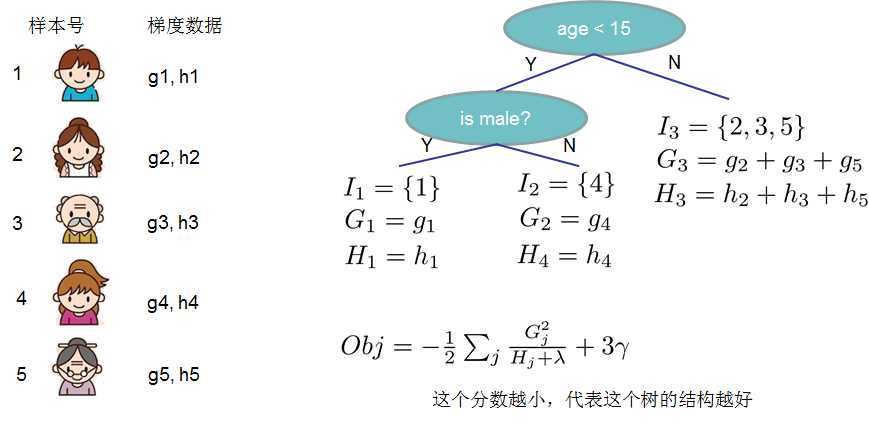
树的生长是从一个节点不断分裂的过程,关键在于节点如何分裂?
理想情况下,每一次分裂都要计算所有特征的所有样本的切分所得到的结构分数,选择最好的特征做切分,然后每个叶子再重新完整计算一遍所有切分情况的结构分数,直到找到最优树结构,但是这样非常不现实,所以xgboost提出两种切分策略:贪心法和近似算法。
先遍历所有特征,对特征下面的值进行排序,线性扫描确定最优的切分点,由Gain值来评估切分候选项。


当数据量很大时,不可能将全部数据读到内存中,或者在分布式计算中无法预先排序,这时候需要近似算法。近似算法根据特征的统计分布的一些百分位点来作为分割点,连续的样本会被分到这些点切出来的桶中,最后汇总统计数据找到最佳分裂点。
关于找到分裂点还有两种方案,一种是全局的,在一开始就计算好所有的最优分割点,在后面树生长的时候就用这个已经计算好的相同的分割点;一种是局部的,是在每一次进行分割的时候都计算一遍最优的点。全局的计算量要比局部的计算量小,但是全局的通常需要分出更多的桶才能达到比较好的效果。局部的方式更适合更深的树。
分桶的策略可以使用梯度近似直方图实现(approximate histograms of gradient statistics)

在近似算法中的重要步骤是如何确定候选分裂点。通常特征值的百分位被用于生成候选分裂点。令集合
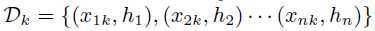
表示第k个特征的每个训练样本的二阶梯度统计。定义一个排序函数:
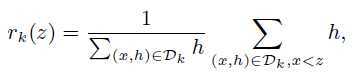
表示特征值k小于z的比例,目标是寻找候选分裂点集${ s_{k1},s_{k2},...,s_{kl} }$。因此
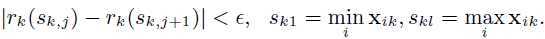
这里$\epsilon$是近似因子,这意味着有大概$\frac{1}{\epsilon}$个候选点。这里每个数据点的权重为$h_{i}$
由于数据中有缺失值、0统计值和onehot,造成训练数据稀疏,xgboost用了一个default以便处理稀疏数据。它有两个缺省划分方向,通过从数据中学习来找到最优的缺省方向。
shrinkage是为了防止过拟合的一个技巧。
每一轮树增长后,要乘以一个权重系数$\eta$,类似学习率的感觉,它缩减了每棵树的影响。
列抽样加速了并行算法的计算
效果比行抽样要好(样本抽样)
防止了过拟合
https://zhuanlan.zhihu.com/p/31654000
https://www.pianshen.com/article/5176891606/
https://blog.csdn.net/v_JULY_v/article/details/81410574
XGBoost论文
原文:https://www.cnblogs.com/4PrivetDrive/p/12915666.html