Not So Simple Polygon Embedding

题意：

给出 \(n\)，为奇数。求覆盖边数为 \(2n\) 的正凸多边形的最小正方向的边长，多边形的边长为 \(1\)。

分析：

（借用题解的图）

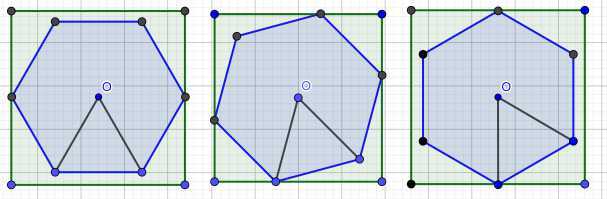
对于一个正多边形，设个顶点与中心连线形成的每个小三角形的顶角为 \(\theta\)，假设多边形旋转角度为 \(\alpha\)，由于对称性，旋转角度在 (\(\theta\),\(\alpha\)] 是无效的。
在此范围内，当 \(\alpha\) 等于 \(0\) 和 \(\theta /2\)的情况实际是一样的，即离中心距离最远的顶点的距离最大。可以发现，最小和最大的变化是对称的，最优解在中间位置取。

代码：

#include <bits/stdc++.h>
using namespace std;
const double pi=acos(-1);
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        double t1=cos(pi/(4.0*n));
        double t2=sin(pi/(2.0*n));
        double ans=t1/t2;
        printf("%.9f\n",ans);
    }
    return 0;
}

推荐博客，其中有详细的讲解和证明，及如何作一个多边形的最小覆盖的正方形。
https://www.cnblogs.com/stelayuri/p/12906790.html

Not So Simple Polygon Embedding

原文：https://www.cnblogs.com/1024-xzx/p/12907655.html