逻辑回归(Logistic Regression)

一、Sigmod函数

线性回归的假设函数:，但在分类问题中需要求输入范围在（0，1），则需要为分类问题寻找另外假设函数。

Sigmod函数式：

，函数值域（0，1）

函数图像

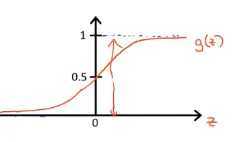
该函数具有很强的鲁棒性,并且将函数的输入范围(∞,-∞)映射到了输出的(0,1)之间且具有概率意义。将一个样本输入到我们学习到的函数中,输出0.7,意思就是这个样本有70%的概率是正例,1-70%就是30%的概率为负例。

所以将线性回归假设函数替换Sigmod函数自变量得：

，表示预测为正例的概率，，则表示预测为负例的概率。

二、逻辑回归损失函数

单样本预测正确的概率:

此时我们需要一组??，使所有样本预测正确的概率最大。根据最大似然估计，最大化似然函数求参数。

似然函数：

则：

为方便计算，似然函数两边同时取对数，可得：

通常我们习惯最小化损失函数，所以在前面加上符号可得交叉熵损失函数：

是关于的高阶可导连续凸函数，根据梯度下降求解。

三、总结

逻辑回归属于广义的线性模型，并通过极大似然估计推导交叉熵损失函数，我们得到的参数值是所有样本被预测正确的概率最大时的参数值，因为所有样本被预测正确的概率更加依赖于多数类别的分类正确与否，然而实际业务情况中，我们常常其实更关注的是少数类别的分类正确情况。

所以认为逻辑回归对正负例样本不均衡比较敏感。

推荐地址https://blog.csdn.net/jk123vip/article/details/80591619?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

逻辑回归(Logistic Regression)

原文：https://www.cnblogs.com/fuyusheng/p/12930301.html