基于数据、构建概率统计模型、进行预测。
学习是一个系统不断优化的过程,统计学习就是计算机系统通过运用数据及统计方法提高系统性能的机器学习。
统计学习三要素:模型、策略、算法
数据,数据起到算法迭代更新的效果,且大数据具有多维度、数据量大等特点时,能够更好的用于机器学习
大数定理,假设数据独立同分布,模型在同一假设空间
1.监督学习(标注数据):学习输入到输出的映射的统计规律。
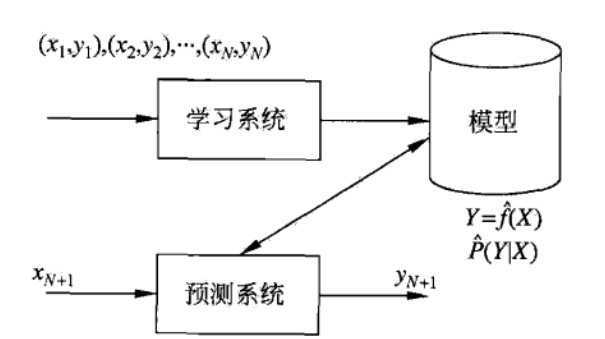
输入空间-->特征空间-->输出空间。
2.非监督学习:无标注数据中学习预测模型,用户发掘统计规律和数据的潜在结构
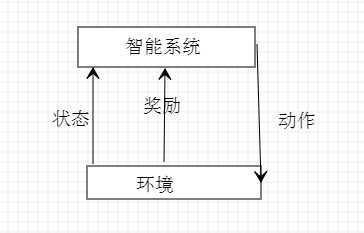
3.强化学习:在智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。
智能系统的目标不是短期奖励的最大化,而是长期累积奖励的最大化。强化学习过程中,系统不断的试错,以达到学习最优策略的目的(从所有可能的策略中选出价值函数最大的策略)
例子:马尔科夫不确定模型可见详情链接
条件概率分布最大化得到函数
函数归一化后得到条件概率分布(根据函数的不同,又可以分为线性和非线性)
概率模型与非概率模型的区分不在于输入与输出的映射关系。而在于模型的内在结构
贝叶斯学习:利用贝叶斯定理,计算在给定数据条件下模型的条件概率(已知东西被偷),并应用贝叶斯定理对数据进行预测(到底是谁偷的)
朴素贝叶斯和潜在狄利克雷分配都属于贝叶斯学习
贝叶斯和最大似然估计的不同:参数
最大似然估计和贝叶斯估计最大区别便在于估计的参数不同,最大似然估计要估计的参数θ被当作是固定形式的一个未知变量,然后我们结合真实数据通过最大化似然函数来求解这个固定形式的未知变量!
贝叶斯估计则是将参数视为是有某种已知先验分布的随机变量,意思便是这个参数他不是一个固定的未知数,而是符合一定先验分布如:随机变量θ符合正态分布等!那么在贝叶斯估计中除了类条件概率密度p(x|w)符合一定的先验分布,参数θ也符合一定的先验分布。我们通过贝叶斯规则将参数的先验分布转化成后验分布进行求解!
同时在贝叶斯模型使用过程中,贝叶斯估计用的是后验概率,而最大似然估计直接使用的是类条件概率密度。
核函数:是映射关系的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
二维映射到三维,区分就更容易了,这是聚类、分类常用核函数的原因。
显式定义从输入空间(低维空间)到特征空间(高维空间)的映射,在特征空间中进行内积计算。例如支持向量机,把输入空间的线性不可分问题转化为特征空间的线性可分问题。
模型的假设空间包含所有可能的条件概率分布或决策函数。
模型属于由输入空间到输出空间的映射的集合,这个集合属于**假设空间**,假设空间为函数族,就是相当于有很多备选模型。
按照怎么样的准则学习或选择最优模型,从假设空间中选择最优模型。
0-1损失(分类)、平方损失(回归)、绝对损失(回归)、对数损失(条件)
期望风险:模型关于联合分布的期望损失
经验风险:模型关于训练样本集的平均损失,根据大数定理,经验风险趋于期望风险
2 风险函数:函数度量平均意义下模型预测的好坏(现实中由于训练样本数量有限,甚至很小,所以用经验风险估计期望风险常常并不理想,因此要对经验风险进行一定的矫正)
(1)经验风险最小化(empirical risk minimization ERM),经验风险最小化的就是最优模型。比如,极大似然估计就是经验风险最小化的一个例子
(2)结构风险最小化(structural risk minimization SRM),是为了防止过拟合(样本空间较小时)而提出的。可以等价于正则化(惩罚)。例如,贝叶斯估计中的最大后验概率估计就是结构风险最小化的例子。当模型是条件概率分布、损失函数时对数函数、模型复杂度有模型的后验概率表示时,结构风险最小化等价于最大后验概率估计。
考虑用什么计算方法得到最优解模型
原文:https://www.cnblogs.com/Towerb/p/12939278.html