今天在网上看到字节的一个概率面试题:
一段绳子剪成三段,求能组成三角形的概率
很像我们初中的知识,由三角形定理我们可知:任意两边之和大于第三边
设绳长为n,一条绳为x,另一条为y,则第三条绳长为(n-x-y)
列方程:
由第一条式子推出:\(2(x+y)>n\) == > \(x+y>\frac{n}{2}\)
再结合其他式子推出:
用desmos画出上面的图形,就是下面的条纹格的三角形,代表能组成三角形
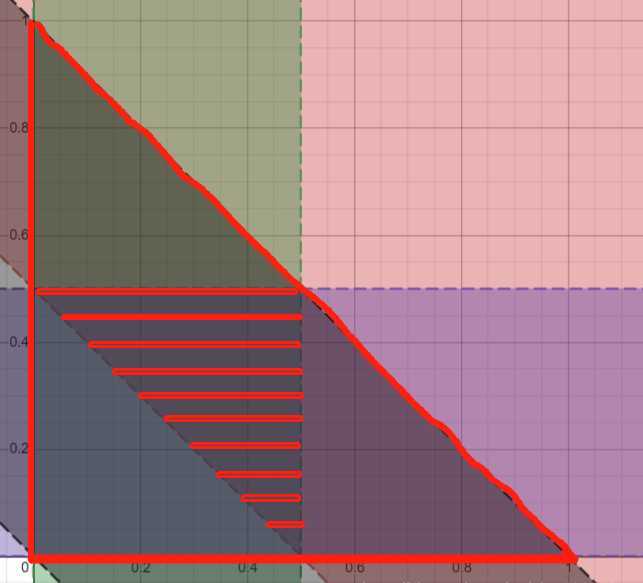
我们再将不能组成三角形的条件考虑进去,\(0<n-x-y<n\),画出大三角形,包括了能组成三角形和不能组成三角形,显而易见,条纹三角形占大三角形面积的\(\frac{1}{4}\)
即随意三段能组成三角形的概率是:\(\frac{1}{4}\)
原文:https://www.cnblogs.com/yeweiqiang/p/12940110.html