该系列为DR_CAN Advanced控制理论视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
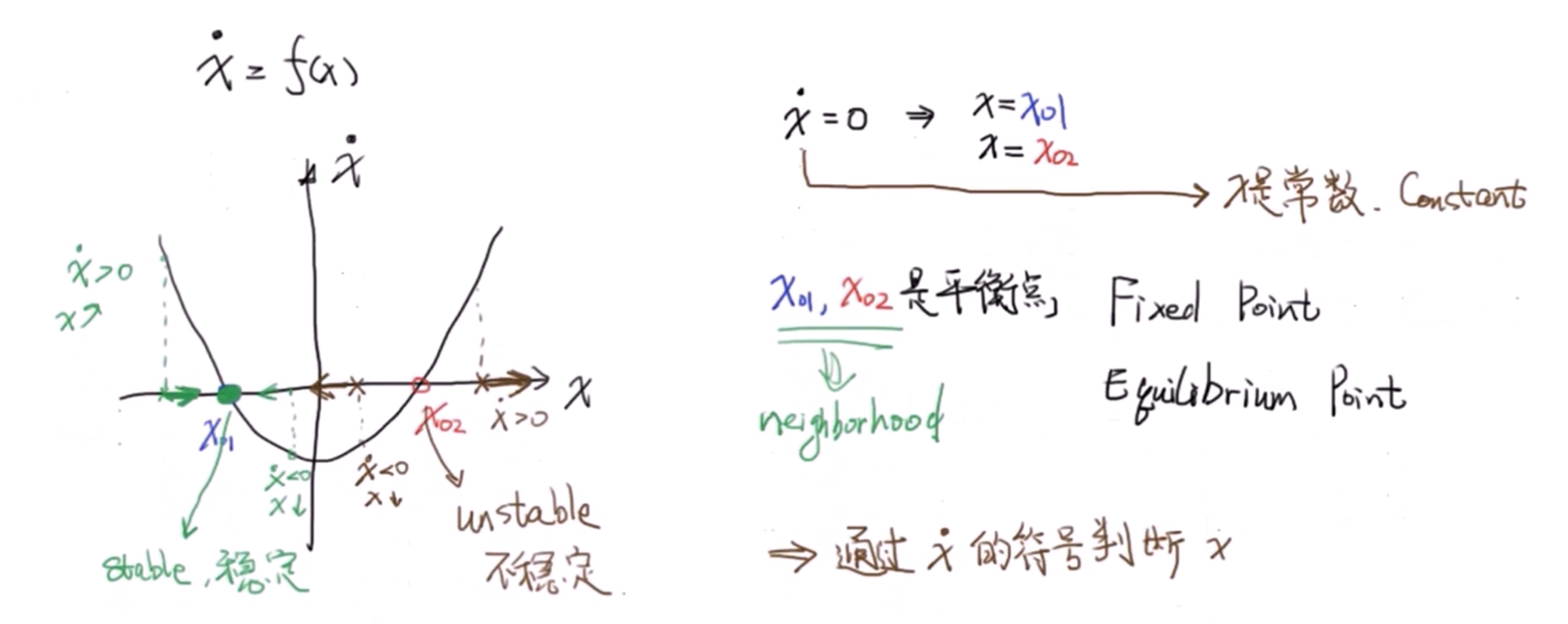
一个简单的例子:注意平衡点与稳定点的区别:
另一个例子,这里并不是标准的相图,因为 \(x-\cos x\) 不好画,因此图中单独绘制了两条曲线,分析其差值即可:
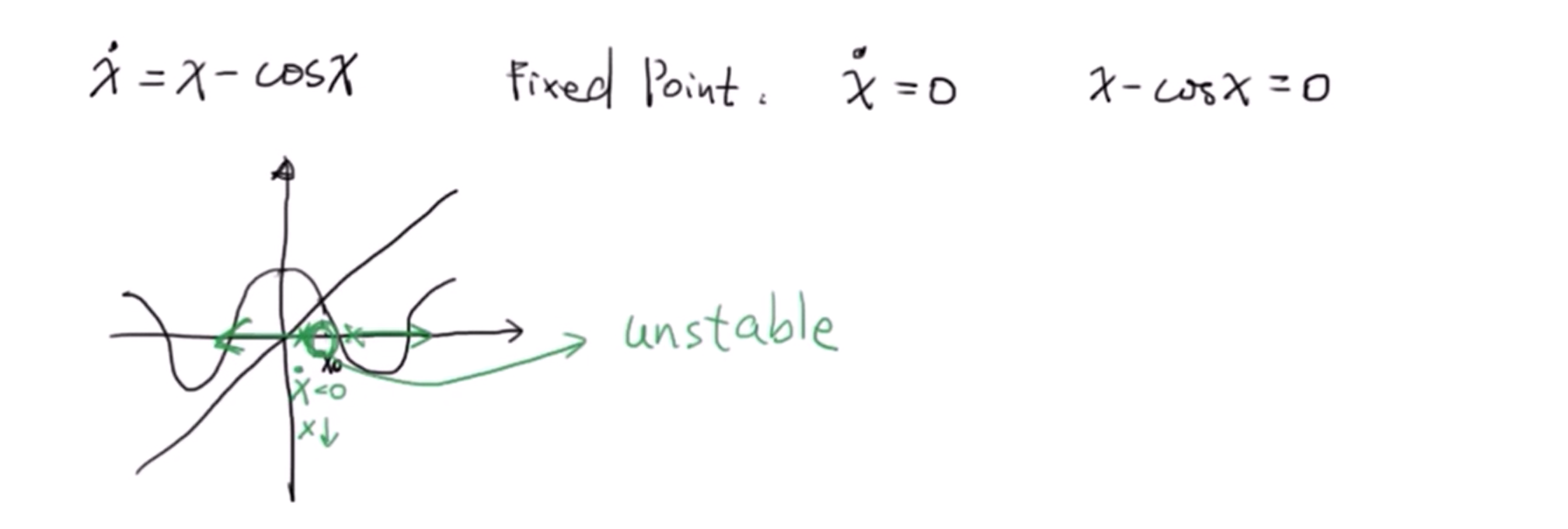
令 \(b=c=0\) 求其平衡点:

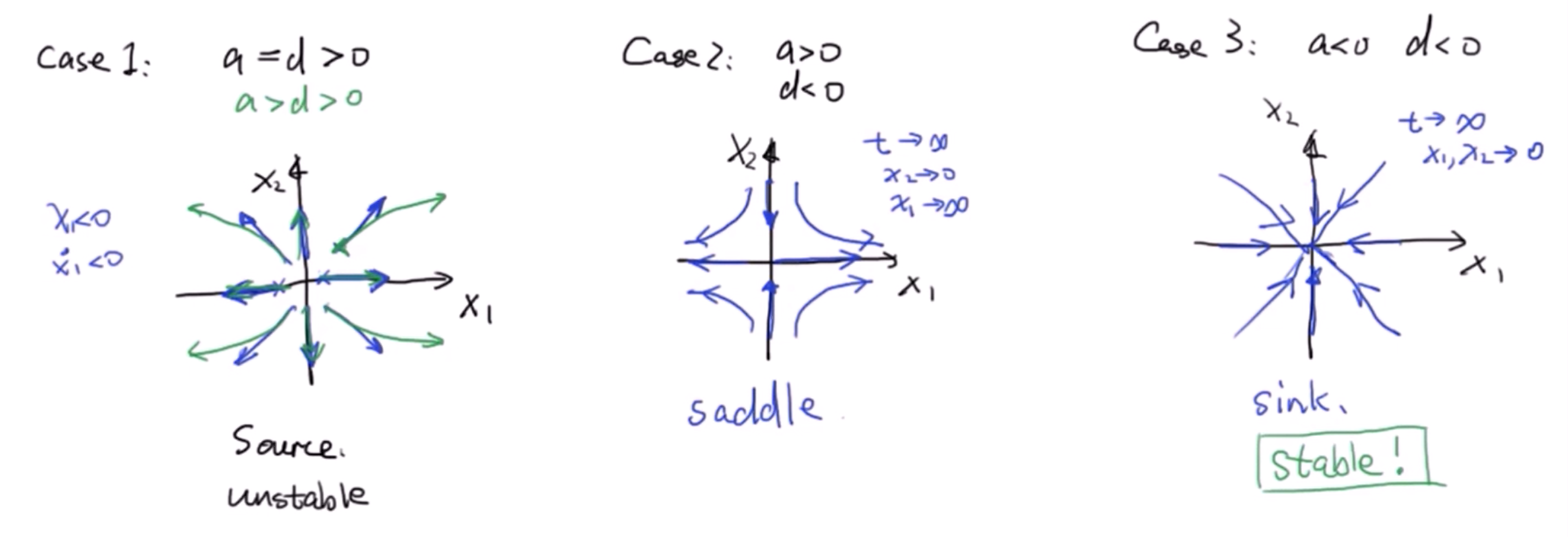
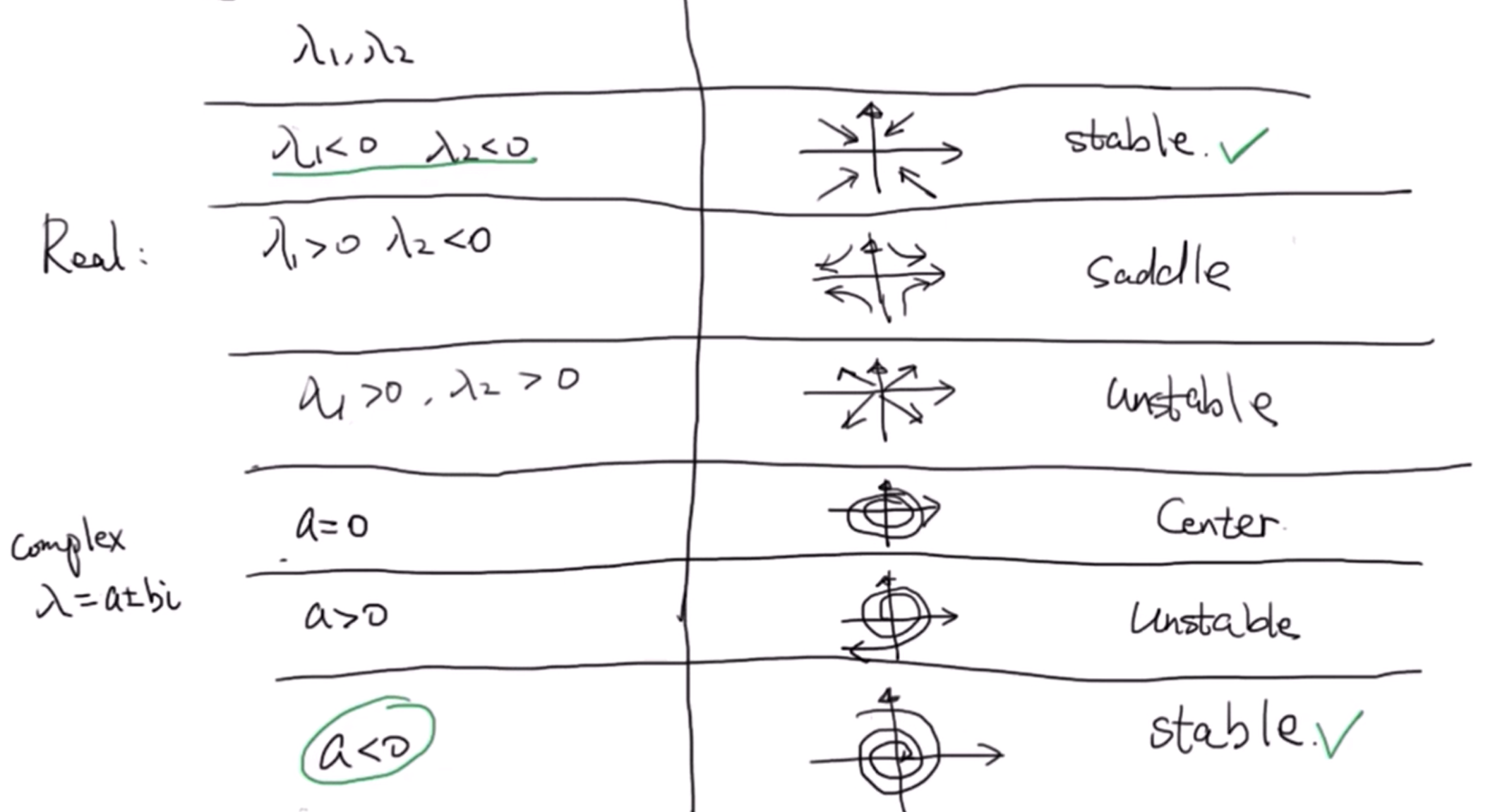
三种特殊情况,三个点分别叫source、saddle、sink:
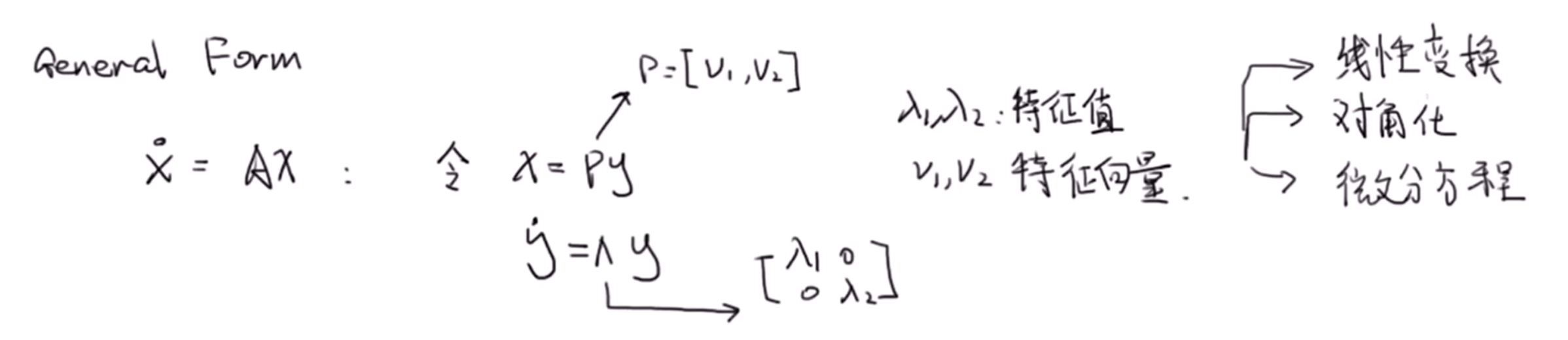
以上是三种特殊情况,下面是一般形式的分析,首先回顾如何通过特征值与特征向量求解微分方程组:

计算实际例子,这里我们用特征值与特征向量求解这个微分方程组。需要注意的是这里的y和系统输出y不是一个y。通过分析y的相图我们可以得到y的性质,而向量x与y为线性变换的关系,实际上把基变换到了特征向量上。这样我们可以通过绘制出特征向量来进一步绘制出x的相图:

我们发现x与y的性质是相同的,也就是说我们可以通过分析A矩阵的特征值来分析系统的稳定性。
某些矩阵可能没有实特征值,而复特征值对应的特征向量是没有方向的。这时我们求出先根据特征向量求出 \(x_1\) \(x_2\) 的值,然后通过欧拉公式展开成三角函数形式。考虑到当线性微分方程的解是由两个项相加而成时,每一个项单独拿出来都是微分方程的解。因此我们可以我们去掉复数部分,可以得到 \(x_1\) \(x_2\) 满足一个椭圆的方程,也就是说在特征值是纯虚数的情况下系统的相图是一个椭圆:

至于椭圆的方向我们可以任取一个特殊位置来判断:
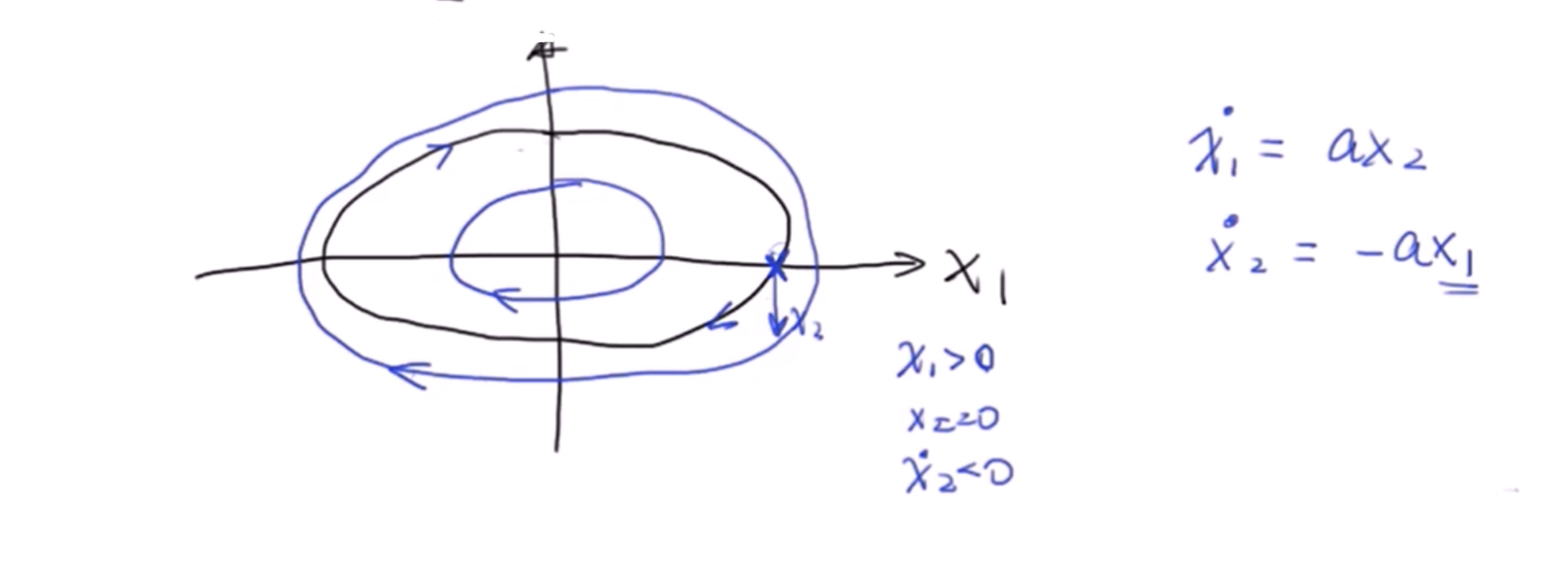
我们发现在这种情况下 \(x_1\) \(x_2\) 的变化是一个循环往复的情况。
这里特征值既包含实部也包含虚部,写出向量y的表达式,由于x与y的性质是相同的因此这里不再像上一个例子那样求向量 \(x_1\) \(x_2\) 的值了。根据上一个例子我们知道 \(e^{2it}\) 与 \(e^{-2it}\) 在相图中表示为圆,而 \(e^t\) 意味着随时间的增加而不断增大,因此该相图应为向外的螺旋线。同样的,螺旋方向也可以根据上一个例子中的方法,即选取特殊点来判断:
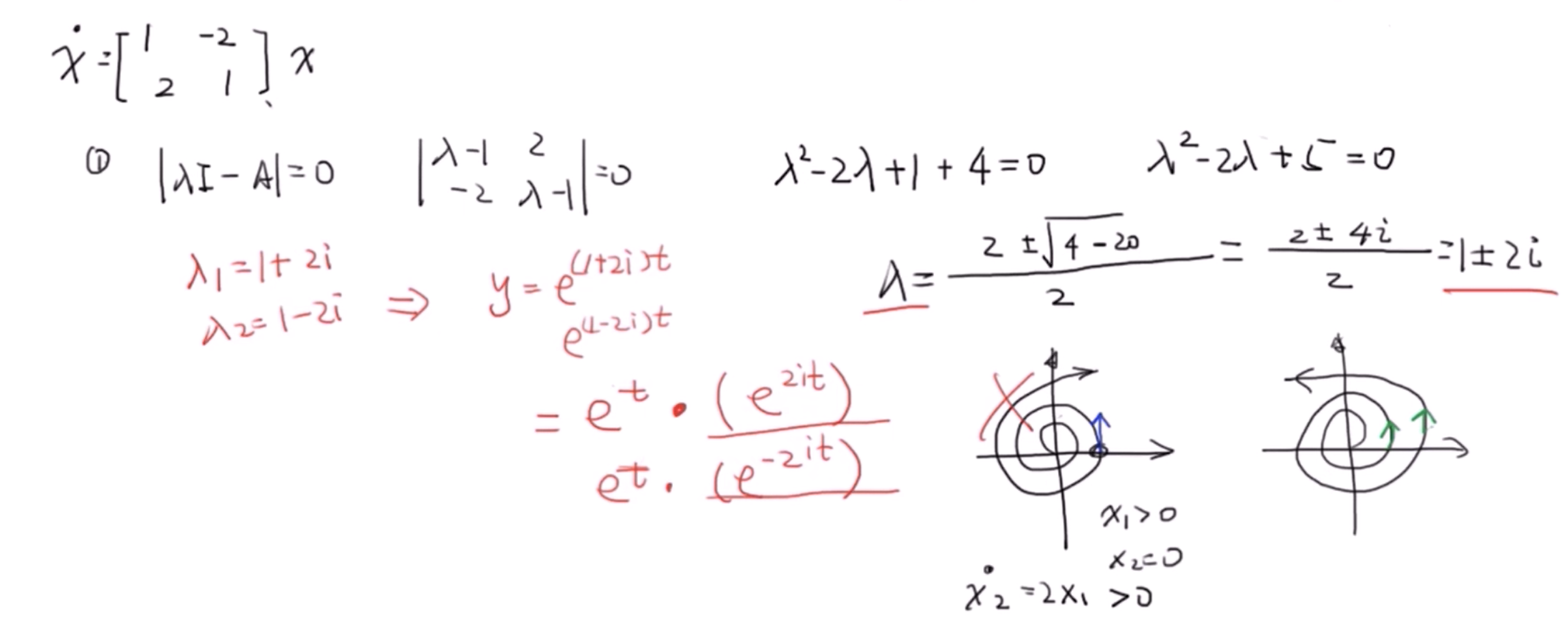
原文:https://www.cnblogs.com/HongxiWong/p/12940411.html