今天拜读徐波老师的《golang从入门到实践》书籍中看到一个小例子,使用golang来实现二维矢量模拟玩家移动。其中介绍在游戏中,一般使用二维矢量保存玩家的位置 。 使用矢量运算计算玩家移动的位置。 觉得很有趣,和大家分享一下。
二维矢量拥有两个方向的信息 ,同时可以进行加、 减、乘 (缩放)、距离 、 单位化等计算 。我们先使用拥有 X 和 Y 两个分量的 Vec2 结构体实现这个二维矢量(即数学中向量)的概念 。
package main
import (
"math"
)
// 位置坐标结构体
type Vec2 struct {
X, Y float32
}
// 使用矢量加上另外一个矢盘,生成新的矢量
func (v Vec2) Add(other Vec2) Vec2 {
return Vec2{
v.X + other.X,
v.Y + other.Y,
}
}
// 减
func (v Vec2) Sub(other Vec2) Vec2 {
return Vec2{
v.X - other.X,
v.Y - other.Y,
}
}
// 乘
func (v Vec2) Scale(s float32) Vec2 {
return Vec2{v.X * s, v.Y * s}
}
// 计算两个矢量的距离
func (v Vec2) DistanceTo(other Vec2) float32 {
dx := v.X - other.X
dy := v.Y - other.Y
return float32(math.Sqrt(float64(dx*dx + dy*dy)))
}
// 返回当前矢量的标准化矢量
func (v Vec2) Normalize() Vec2 {
mag := v.X*v.X + v.Y*v.Y
if mag > 0 {
oneOverMag := 1 / float32(math.Sqrt(float64(mag)))
return Vec2{v.X * oneOverMag, v.Y * oneOverMag}
}
return Vec2{0, 0}
}
(1) 使用矢量减法,将目标位置( targetPos )减去当前位置( currPos )即可计算出位于两个位置之间的新矢量。
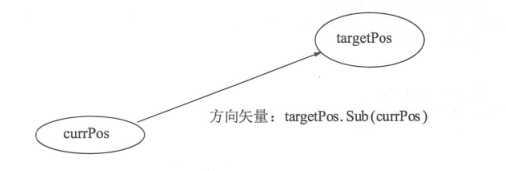
(2)使用 Nonnalize() 方法将方向矢量变为模(长度)为1的单位化矢量。 这里需要将矢量单位化后才能进行后续计算。
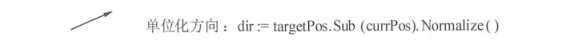
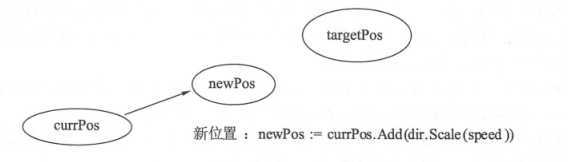
(3)获得方向后,将单位化方向矢量根据速度进行等比缩放,速度越快,速度数值越大,乘上方向后生成的矢量就越长(模很大)。

(4) 将缩放后的方向 添加到 当前位置后形成新的位置 。
// 玩家
type Player struct {
currPos Vec2 //当前位置
targetPos Vec2 //目标位置
speed float32 //移动速度
}
// 设置玩家移动的目标位置
func (p *Player) MoveTo(v Vec2) {
p.targetPos = v
}
// 玩家当前位置
func (p *Player) Pos() Vec2 {
return p.currPos
}
// 是否到达目的地
func (p *Player) IsArrived() bool {
// 通过计算当前玩家位置与目标位置的距离不超过移动的步长,判断已经到达目标点
return p.currPos.DistanceTo(p.targetPos) < p.speed
}
// 更新玩家的位置
func (p *Player) Update() {
if !p.IsArrived() {
// 计算当前位置指向目标的朝向
dir := p.targetPos.Sub(p.currPos).Normalize()
// 添加速度矢量生成新的位置
newPos := p.currPos.Add(dir.Scale(p.speed))
// 移动完成后,更新当前位置
p.currPos = newPos
}
}
// 创建新玩家
func NewPlayer(speed float32) *Player {
return &Player{
speed: speed,
}
}
func main() {
p := NewPlayer(0.5)
p.MoveTo(Vec2{3, 5})
for !p.IsArrived() {
p.Update()
fmt.Println(p.Pos())
}
}
运行结果:
{0.2572479 0.4287465}
{0.5144958 0.8574929}
{0.77174366 1.2862394}
{1.0289915 1.7149858}
{1.2862394 2.1437323}
{1.5434873 2.5724788}
{1.8007352 3.0012252}
{2.0579832 3.4299717}
{2.315231 3.8587182}
{2.572479 4.2874646}
{2.8297267 4.7162113}
总结:
首先我们实现一个矢量结构 Vec2 来保存玩家的位置坐标,并为这个结构定义了加、减、乘、单位化方法。使用这一系列矢量运算计算出玩家移动的位置。
然后我们实现一个玩家对象,定义玩家的当前位置 、目标位置和速度属性,为这个对象实现操作她的方法,比如设置目的地,更新位置等来模拟玩家的移动。
在更新玩家位置逻辑中计算当前位置指向目标的朝向时,先将两矢量相减获得指向被减矢量的新矢量。然后将新矢量使用 Normalize()方法单位化 。最终返回的 dir 矢量就是移动方向(因为单位化后模为1)。这个dir矢量和速度属性配合计算玩家移动后的新位置。
在IsArrived方法中判断玩家是否到达目标点。玩家每次移动的半径就是速度( speed ),因此,如果当前位置与目标点的距离小于速度,表示己经非常靠近目标,可以视为到达目标。
原文:https://www.cnblogs.com/Jimmy00/p/12943707.html