大数四则运算

大数加法

两个大数相加，分别用字符串s1, s2存储，并使用.size()获取位数（即字符串长度）。

逐位转化为int，然后相加。carry变量用来存储进位。

结果存储在字符串res中。由于最先计算的是低位，所以输出时应该逆序，使高位先输出，得到正确相加结果。

这个代码没有考虑负数的情况，但是其实很简单，当有一个负数时使用下述的大数减法，当两个负数时化为正数相加再加负号即可。代码中就不补充了。

#pragma warning(disable:4996)
#include <iostream>
#include <string>
using namespace std; 

int main() {
	string s1, s2, res;
	int len1, len2, reslen, carry = 0;
	//输入大数字符串
	cin >> s1;
	cin >> s2;
	//取得大数位数，即字符串长度
	len1 = s1.size();
	len2 = s2.size();
	//逐位相加，carry用来存储进位
	for (reslen = 0; ; reslen++) {
		if (len1 <= reslen && len2 <= reslen) break;
		int temp, temp1 = 0, temp2 = 0;
		if (len1 > reslen) temp1 = int(s1[len1 - 1 - reslen]) - 48;
		if (len2 > reslen) temp2 = int(s2[len2 - 1 - reslen]) - 48;
		temp = temp1 + temp2 + carry;
		carry = temp / 10;
		res = res + char(temp % 10 + 48);
	}
	//如果多余进位为1，加入res结果中
	if (carry == 1 ) {
		res = res + ‘1‘;
		reslen++;
	}
	//逆位打印输出
	for (int i = res.size() - 1; i >= 0; i--) {
		cout << res[i];
	}
	cout << endl;
}

• 测试

输入：

111111111111111111111111111111111111111111111111
999999999999999999999999999999999999999999999999999999999999999999999999

输出：

1000000000000000000000000111111111111111111111111111111111111111111111110

?

大数减法

与大数加法类似。

两个大数相减，分别用字符串s1, s2存储，同时比较大小，若s1小于s2，结果为负数。交换，使得s1大于s2，置negtive为1。

s1逐位减去s2，carry变量用来存储从大一位借来的数

判断negtive的值，为1时则结果为负数。

在逆序输出前，先使用一个循环消除不应该显示的先导0。

同样没有考虑负数输入，当有负数输入时只需插入一个判断，做简单的预处理即可。

#pragma warning(disable:4996)
#include <iostream>
#include <string>
#include <algorithm>
using namespace std; 

int main() {
	string s1, s2, res;
	int len1, len2, reslen, carry = 0, negtive = 0;
	//输入大数字符串
	cin >> s1;
	cin >> s2;
	//使s1为大，s2为小
	if ((s1.length() < s2.length()) || (s1.length() == s2.length() && s1 < s2)) {
		swap(s1, s2);
		negtive = 1;
	}
	//取得大数位数，即字符串长度
	len1 = s1.length();
	len2 = s2.length();
	//逐位相减，carry用来存储借位
	for (reslen = 0; reslen < len1; reslen++) {
		int temp, temp1 = 0, temp2 = 0;
		temp1 = int(s1[len1 - 1 - reslen]) - 48;
		if (len2 > reslen) temp2 = int(s2[len2 - 1 - reslen]) - 48;
		temp = temp1 - carry - temp2;
		if (temp < 0) {
			temp = temp + 10;
			carry = 1;
		}
		else {
			carry = 0;
		}
		res = res + char(temp + 48);
	}
	//如果多余进位为1，加入res结果中
	if (negtive == 1 ) {
		cout << ‘-‘;
	}

	//逆位打印输出
	int a;
	for (a = res.size() - 1; a > 0; a--) {
		if (res[a] != ‘0‘) break;
	}
	for (int i = a; i >= 0; i--) {
		cout << res[i];
	}
	cout << endl;
}

• 测试

输入：

111111111111111111111111111111111111111111111111
1000000000000000000000000111111111111111111111111111111111111111111111110

输出：

-999999999999999999999999999999999999999999999999999999999999999999999999

?

大数乘法

计算的过程基本上和小学生列竖式做乘法相同，逐位相乘。

为编程方便，并不急于处理进位，而将进位问题留待最后统一处理。

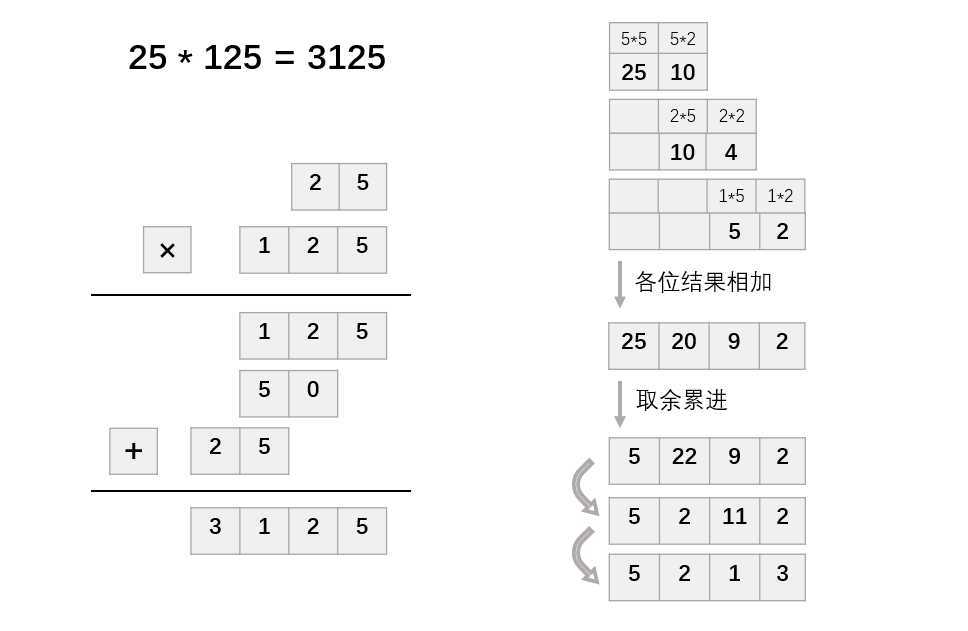
#pragma warning(disable:4996)
#include <iostream>
#include <string>
#include <vector>
using namespace std; 

int main() {
	vector<int> res;
	string s1, s2;
	int len1, len2, reslen;
	//输入，获取长度（位数）
	cin >> s1;
	cin >> s2;
	len1 = s1.length();
	len2 = s2.length();
	//逐位相乘、相加
	int loc_m = 0, loc_n = 0;
	//s1(乘式下面一行）
	for (int i = len1 - 1; i >= 0; i--) {
		loc_m = loc_n++;
		//s2(乘式上面一行）
		for (int j = len2 - 1; j >= 0; j--) {
			if (res.size() <= loc_m) {
				res.push_back(int(s1[i] - 48)*int(s2[j] - 48));
			}
			else {
				res[loc_m] += int(s1[i] - 48)*int(s2[j] - 48);
			}
			loc_m++;
		}
	}
	//处理进位
	int k;
	for (k = 0; k < res.size()-1; k++) {
		res[k + 1] += res[k] / 10;
		res[k] = res[k] % 10;
	}
	for (;;k++) {
		if (res[k] >= 10) {
			res.push_back(res[k] / 10);
			res[k] = res[k] % 10;
		}
		else break;
	}
	//逆序输出
	for (int i = res.size() - 1; i >= 0; i--) {
		cout << res[i];
	}
	cout << endl;
}

• 测试

输入：

9999999999
9999999999

输出：

99999999980000000001

?

大数除法

单独的除法比较简单，减去被除数倍数即可
大数除法+进制转换

大数四则运算

原文：https://www.cnblogs.com/maeryouyou/p/12945012.html