
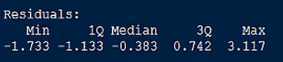
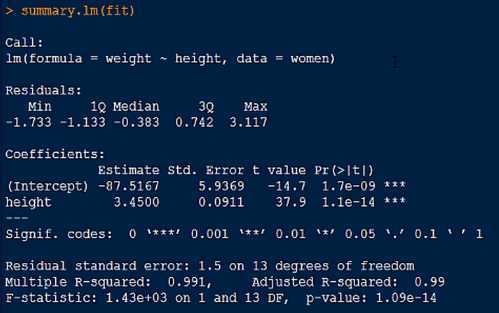
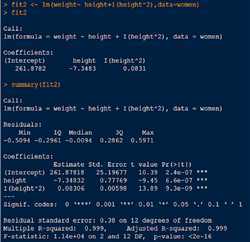
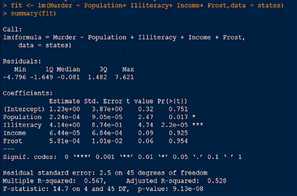
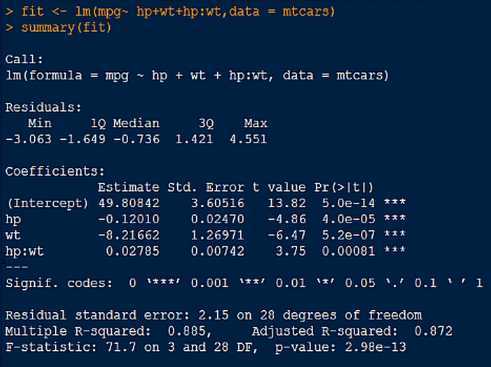
残差是真实值与预测值之间的差,五个分位的值越小模型越精确
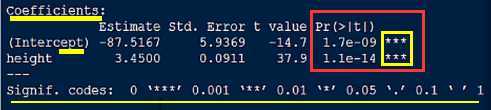
残差的标准误差,越小越好
模型拟合的质量判定指标,取值在0-1之间,值越大越好
Multiple R-squared: 0.991 表示该模型能解释99.1%的数据。
说明模型是否显著,值越小越好,说明模型越显著
先看F统计量是否小于0.05,如果小于0.05,再看R方判定系数。
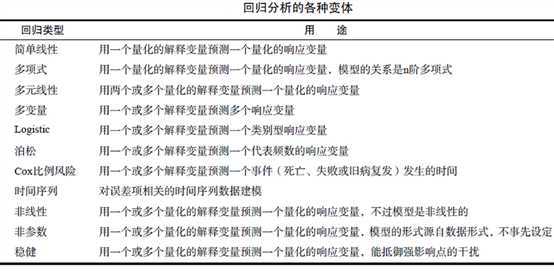
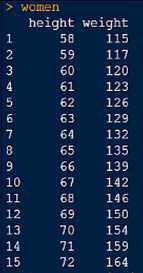
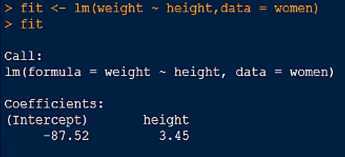
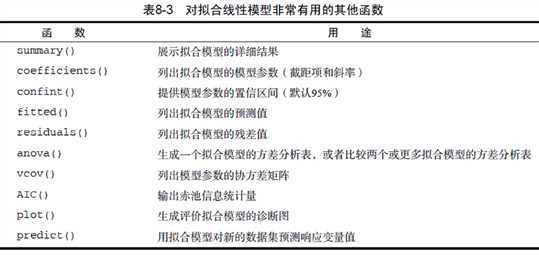
回归(regression),通常指那些用一个或多个预测变量,也称自变量或解释变量来预测响应变量,也称为因变量、校标变量或结果变量的方法。
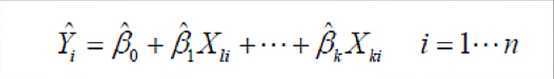

使用 par(mfrow = c(2,2)) 可以将四幅图显示在一个窗口中

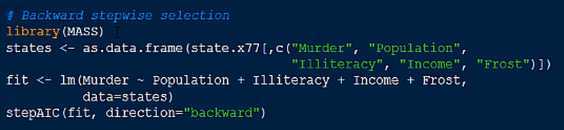
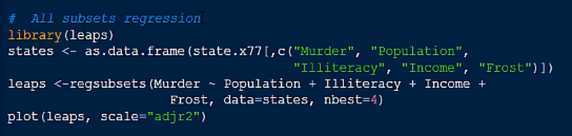
对于固定的自变量值,因变量值成正态分布。
因变量之间相互独立
因变量与自变量之间为线性相关
因变量的方差不随自变量的水平不同而变化。也可称作不变方差。
方差分析,称为Analysis of Variance,简称ANOVA ,也称为"变异数分析”, 用于两个及两个以上样本均数差别的显著性检验。从广义上来讲,方差分析也属于回归分析的一-种。只不过线性回归的因变量一-般是连续型变量。而当自变量是因子时,研究关注的重点通常会从预测转向不同组之间差异的比较。这就是方差分析。



功效分析, power analysis,可以帮助在给定置信度的情况下,判断检测到给定效应值时所需的样本量。反过来,它也可以在给定置信度水平情况下,计算在某样本量内能检测到给定效应值的概率。
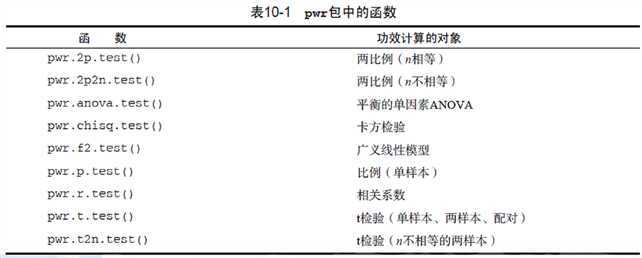

●样本大小指的是实验设计中每种条件/组中观测的数目。
●显著性水平 (也称为alpha )由型错误的概率来定义。也可以把它看做是发现效应不发生的概率。
●功效通过I减去I型错误的概率来定义。我们可以把它看做是真实效应发生的概率。
●效应值指的是在备择或研究假设 下效应的量。效应值的表达式依赖于假设检验中使用的统计方法。
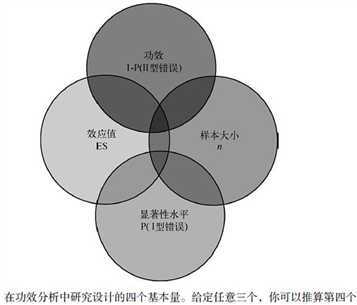
线性回归和方差分析都是基于正态分布的假设,广义线性模型扩展了线性模型的框架,它包含了非正态因变量的分析。
泊松回归是用来为计数资料和列联表建模的一种回归分析。泊松回归假设因变量是泊松分布,并假设它的平均值的对数可被未知参数的线性组合建模。
当通过一系列连续型或类别型预测变量来预测二值型结果变量时,Logistic回归效果会很好
根据危险因素预测某疾病发生的概率。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即是”或“否”,为两分类变量,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门]螺杆菌感染等。自变量既可以是连续的, 也可以是分类的。通过logistic回归分析 ,就可以大致了解到底哪些因素是胃癌的危险因素。
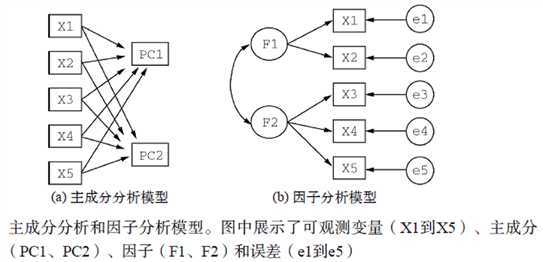
主成分分析,Principal Component Analysis,也简称为PCA,是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关的变量称为主成分。主成分其实是对原始变量重新进行线性组合将原先众多具有一定相关性的指标,重新组合为一组的新的相互独立的综合指标。
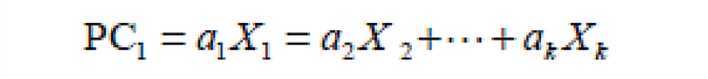
●数据预处理;
●选择分析模型;
●判断要选择的主成分/因子数目;
●选择主成分/因子;
●旋转主成分/因子;
●解释结果;
●计算主成分或因子得分。这步也是可选的。
探索性因子分析法Exploratory Factor Analysis,简称为EFA,是一系列用来发现一组变量的潜在结构的方法。它通过寻找一组更小的、 潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系。
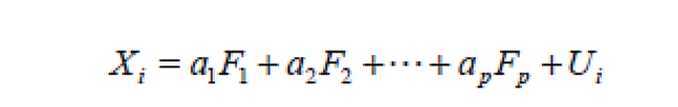
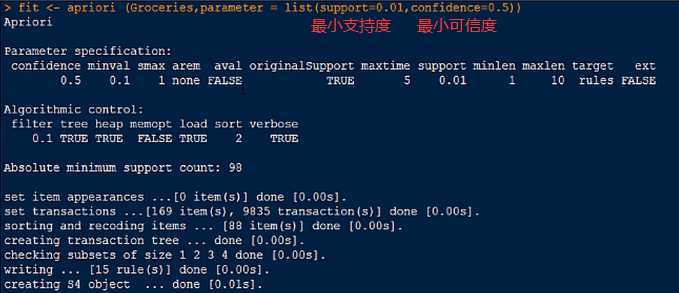
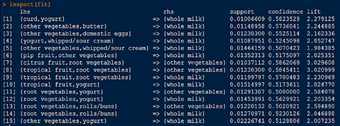
原文:https://www.cnblogs.com/nnadd/p/12942029.html