数组是一种基本的数据结构,用于按顺序存储元素的集合。但是元素可以随机存取,因为数组中的每个元素都可以通过数组索引来识别。
数组可以有一个或多个维度。这里我们从一维数组开始,它也被称为线性数组。如下所示:
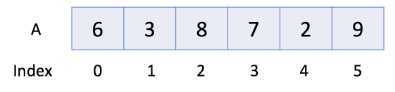
在上面的例子中,数组 A 中有 6 个元素。也就是说,A 的长度是 6 。我们可以使用 A[0] 来表示数组中的第一个元素。因此,A[0] = 6 。类似地,A[1] = 3,A[2] = 8,依此类推。此外,数组一旦定义后,大小不能更改。
// golang中的数组
// 声明一个float32类型且长度为10数组
var balance [10] float32
// 初始化已声明数组
balance = [10]float32{1, 2, 3, 4}
balance[0] = 2
// 声明并定义一个数组
var balance = [10]float32{1, 2, 3, 4}
// 根据元素个数,设置数组长度
var balance = [...]float32{1, 2, 3, 4}
// 只能在函数内使用这种格式
balance := [...]float32{1, 2, 3, 4}
// 遍历数组
func main() {
var a = [...]string{"北京", "上海", "深圳"}
// 方法1:for循环遍历
for i := 0; i < len(a); i++ {
fmt.Println(a[i])
}
// 方法2:for range遍历
for index, value := range a {
fmt.Println(index, value)
}
数组具有固定的容量,我们需要在初始化时指定数组的大小。有时它会非常不方便并可能造成浪费。
因此,大多数编程语言都提供内置的动态数组,它仍然是一个随机存取的列表数据结构,但大小可变。
在Golang中为切片(slice),它非常灵活,支持自动扩容。
// 声明切片
var slice []float32
// 初始化切片
slice = []float32{1, 2, 3, 4}
// 声明+初始化
var slice = []float32{1, 2, 3, 4}
// 只能在函数内使用这种格式
slice := []float32{1, 2, 3, 4}
// 用make来创建切片 ---> make([]T, length, capacity)
var slice []float32 = make([]float32, 5, 10)
slice := make([]float64, 5, 10)
// 常用函数
len(slice) // 长度
cap(slice) // 容量
append(slice,要添加元素)
copy(slice1,slice) // slice ---> slice1
下面是关于数组(二维数组)的三个案例**:
给定一个整数类型的数组 nums,请编写一个能够返回数组“中心索引”的方法。
我们是这样定义数组中心索引的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
示例 1:
输入:
nums = [1, 7, 3, 6, 5, 6]
输出: 3
解释:
索引3 (nums[3] = 6) 的左侧数之和(1 + 7 + 3 = 11),与右侧数之和(5 + 6 = 11)相等。
同时, 3 也是第一个符合要求的中心索引。
示例 2:
输入:
nums = [1, 2, 3]
输出: -1
解释:
数组中不存在满足此条件的中心索引。
说明:
nums 的长度范围为 [0, 10000]。nums[i] 将会是一个范围在 [-1000, 1000]的整数。func pivotIndex(nums []int) int {
sum := 0
leftSum := 0
for _,i := range nums {
sum += i
}
for k,v := range nums {
if leftSum == sum - v - leftSum {
return k
}
leftSum += v
}
return -1
}
在一个给定的数组nums中,总是存在一个最大元素 。
查找数组中的最大元素是否至少是数组中每个其他数字的两倍。
如果是,则返回最大元素的索引,否则返回-1。
示例 1:
输入: nums = [3, 6, 1, 0]
输出: 1
解释: 6是最大的整数, 对于数组中的其他整数,
6大于数组中其他元素的两倍。6的索引是1, 所以我们返回1.
示例 2:
输入: nums = [1, 2, 3, 4]
输出: -1
解释: 4没有超过3的两倍大, 所以我们返回 -1.
提示:
nums 的长度范围在[1, 50].nums[i] 的整数范围在 [0, 100].func dominantIndex(nums []int) int {
index := -1
if len(nums) == 0 { // 数组只有一个数的情况
return index
}
//求出最大值
max := nums[0]
for i, v := range nums {
if v >= max {
max = v
index = i
}
}
for i, _ := range nums {
if i == index{ // 忽略最大值
continue
}
if nums[i]*2 > max {
return -1
}
}
return index
}
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
解:
func plusOne(digits []int) []int {
/*
考察进位为问题
*/
for i := len(digits) - 1; i >= 0; i-- {
// 数组最末元素如果不是9,直接加1返回
// 否则该元素置零,前一项元素加1,以此类推
if digits[i] < 9 {
digits[i]++
return digits
} else {
digits[i] = 0
}
}
// 以上操作都没有返回数组,则证明数组第一个元素也需要进位
// 合并数组
return append([]int{1}, digits...)
}
类似于一维数组,二维数组也是由元素的序列组成。但是这些元素可以排列在矩形网格中而不是直线上。
二维数组是最简单的多维数组,二维数组本质上是由一维数组组成的。二维数组定义方式如下:
var arrayName [ x ][ y ] variable_type
variable_type 为 Go 语言的数据类型,arrayName 为数组名,二维数组可认为是一个表格,x 为行,y 为列,下图演示了一个二维数组 a 为三行四列:
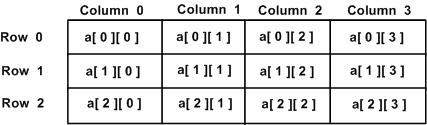
二维数组中的元素可通过 a[i][j]来访问。
练习如下:
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
含义: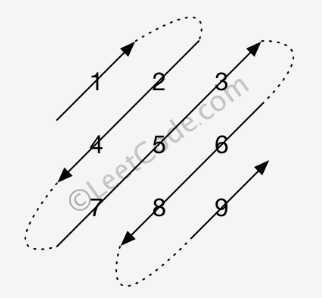
说明:
func findDiagonalOrder(matrix [][]int) []int {
/*
看作一个小球在矩形框格中碰壁移动的情形,共移动i*j次
首先根据行与列之和 i+j 的奇偶确定移动的方向,奇数向右上,偶数向左下。
每次行走方向又有三种边界的情况
1.上边界或者下边界碰壁后向右走,即j+1
2.左边界或者右边界碰壁后向下走,即i+1
3.去他情况:右上遍历:i-1,j+1;左下遍历:i+1;j-1
*/
var result []int // 返回的一维数组
if len(matrix) == 0 { // 二维数组为空
return result
}
rowLen, columnLen := len(matrix), len(matrix[0]) // 二维数组行、列数
i := 0 // 当前所在行
j := 0 // 当前所在列
for k := 0; k < rowLen*columnLen; k++ {
result = append(result, matrix[i][j])
// 行+列 和为偶数时 向右上方遍历,此后分为三种情况
if (i+j)%2 == 0 {
if j == columnLen-1 { // 撞右墙往下走
i++
} else if i == 0 { // 撞最上端墙往右走
j++
} else { // 没撞墙斜着走
j++
i--
}
// 行+列 和为奇数时 向左下方遍历,此后分为三种情况
} else {
if i == rowLen-1 { // 撞下墙往右走
j++
} else if j == 0 { // 撞左墙往右走
i++
} else { // 没撞墙斜着走
j--
i++
}
}
}
return result
}
给定一个包含 m x n 个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
示例 1:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]
示例 2:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]
解:
func spiralOrder(matrix [][]int) []int {
/*
分为四种情况,遍历到左边界,下边界,右边界,上边界
*/
var result []int // 返回的一维数组
if len(matrix) == 0 { // 二维数组为空
return result
}
// 上边界,下边界,左边界,右边界
top, bottom, left, right := 0, len(matrix)-1, 0, len(matrix[0])-1
// 当前位置坐标
i, j := 0, 0
// 运动方向。1表示向右,2:向下,3:向左。4:向上
dir := 1
for top <= bottom && left <= right {
result = append(result, matrix[i][j])
switch dir {
// 1,2,3,4:右,下,左,上
case 1:
if j == right { // 如果到了右端,向下移动1,且上边界+1
dir = 2
i++
top++
continue
}
j++ // 向右移动1
case 2:
if i == bottom { // 如果到了下端,向左移动1,且右边界-1
dir = 3
j--
right--
continue
}
i++ // 向下移动1
case 3:
if j == left { // 如果到了左端,向上移动1,且下边界-1
dir = 4
i--
bottom--
continue
}
j-- // 向左移动1
case 4:
if i == top { // 如果到了上端,向左移动1,且左边界+1
dir = 1
j++
left++
continue
}
i-- // 向上移动1
}
}
return result
}
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
附:在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
解:
func generate(numRows int) [][]int {
// 容量(行)为 numRows
nums := make([][]int,numRows)
for i:=0;i<numRows;i++ {
// 每一行的容量为 i+1
nums[i] = make([]int,i+1)
// 每行第一个元素为 1
nums[i][0] = 1
// 中间元素运算
for j:=1;j<len(nums[i])-1;j++ {
nums[i][j] = nums[i-1][j-1] + nums[i-1][j]
}
// 每行最后一个元素为1
nums[i][i] = 1
}
return nums
}
原文:https://www.cnblogs.com/newbase/p/12953679.html