可数公理

x的邻域基

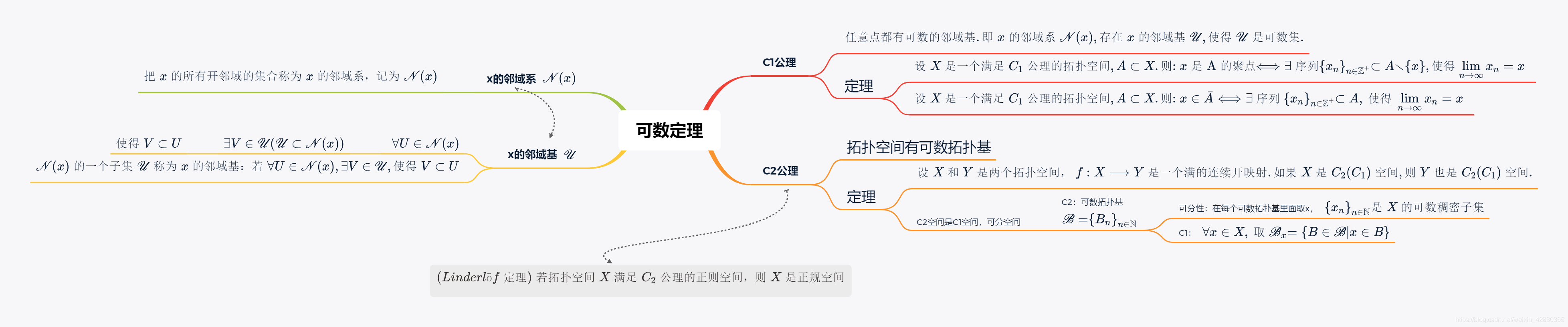
\(\mathscr{N}(x) 的一个子集 \mathscr{U} 称为 x 的邻域基：若 \forall U \in \mathscr{N}(x), 存 在 V \in \mathscr{U}, 使得 V \subset U\)

C1公理

任意点都有可数的邻域基.即 \(x\) 的邻域系 \(\mathscr{N}(x),\) 存在 \(x\) 的邻域基 \(\mathscr{U},\) 使得 \(\mathscr{U}\) 是可数集

C2公理

C2：拓扑空间有可数拓扑基
C2空间是C1空间，可分空间
C2：定义可得可数集\(\mathscr{B}=\left\{B_{n}\right\}_{n \in \mathbb{N}}\)
可分性：
在每个可数拓扑基里面取\(\left\{x_{n}\right\}_{n \in \mathbb{N}}\) 是 \(X\) 的可数稠密子集
с1公理：
\(\forall x \in X,\) 取 \(\mathscr{B}_{x}=\{B \in \mathscr{B} | x \in B\}\)

可数公理

原文：https://www.cnblogs.com/zonghanli/p/12960495.html