[codeforces 903A] Hungry Student Problem 朴素dp:
从小往大判断那些个数可以取得
[codeforces 903B] The Modcrab 贪心:
有血就打,没血回城
[codeforces 903C] Boxes Packing 思维:
相同大小盒子重复出现次数记录下来,最多的那个的次数就是答案
[codeforces 903D] Almost Difference 前缀和+计数:
简单的推公式,坑点是爆longlong,用long double。
[codeforces 903E] Swapping Characters 字符串思维题:
针对第一个字符串进行枚举,方式为将其中两个字符交换,然后和其他字符串比较计算汉明长度,应该都满足等于2,或者等于0的同时字符串中有两个以上的地方是相同字符(这样就可以在交换一次后不改变汉明长度)。具体按以下步骤来就行了。
1.判断所有字符串含有的每个字符的个数是否相等,不等就肯定无解
2. 拿第一个字符串和其他字符串都比对一边,记录字符串中相同位置元素不同的个数如果出现不同元素个数等于1或大于4的情况那么一定无解
3. 对第一个字符串上枚举两个位置做交换,然后这个字符串和其它各字符串的不同元素数如果都满足以下两个条件中任意一个就找到解(比较的时候不要整个字符串都比一遍,技巧看代码)
1)不同个数为2
2)不同个数为0且字符串中存在两个元素相等
4. 在第3步中没有合适的就无解了

char s[2505][5005]; int num0[26], num1[26]; int diff[2505]; int main(){ int k = read(), n = read(); bool flag = false; // 是否有两个位置元素相同 for(int i = 0; i < k; i++) scanf("%s", s[i]); for(int i = 0; i < n; i++) if(++num0[s[0][i] - ‘a‘] == 2) flag = true; for(int i = 1; i < k; i++){ for(int j = 0; j < n; j++) num1[s[i][j] - ‘a‘]++; for(int j = 0; j < 26; j++){ if(num0[j] != num1[j]) {puts("-1"); return 0;} else num1[j] = 0; } } for(int i = 1; i < k; i++){ for(int j = 0; j < n; j++){ if(s[0][j] != s[i][j]) diff[i]++; } if(diff[i] == 1 || diff[i] > 4) {puts("-1"); return 0;} } for(int p1 = 0; p1 < n; p1++){ for(int p2 = p1 + 1; p2 < n; p2++){ bool flag1 = true; for(int i = 1; i < k; i++){ int cnt = diff[i]; cnt -= (s[0][p1] == s[i][p2]); cnt -= (s[0][p2] == s[i][p1]); cnt += (s[0][p1] == s[i][p1]); cnt += (s[0][p2] == s[i][p2]); if(!(cnt == 2 || cnt == 0 && flag)){ flag1 = false; break; } } if(flag1){ swap(s[0][p1], s[0][p2]); cout << s[0] << endl; return 0; } } } puts("-1"); return 0; }
[codeforces 903F] Clear The Matrix 状压dp:
如果我们的操作是从左到右一列一列地消除‘*‘,那么对于其中的某一列的消除,这列的消除能直接影响的只有排在它后面的三列(只能影响到那么远),那么直接将每个四行四列作为一个状态单元(比方说:(1, 1)~(4, 4); (2, 1)~(5, 4))然后状态转移就是单元一列一列往下地推,且前面的列都要消去‘*‘。拿第一个样例举例,第一个状态为(1, 1)~(4, 4),第一列消去三个‘*‘,由于消去的方法有
多种,之后产生的子状态也就有多种,子状态为(2, 1)~(5, 4)。循环往复地向后推,直到(5, 1)~(8, 4),此时前面4列也就全部消去‘*‘了,最小花费也dp出来了。
此外还可以有一步改进:将4行3列作为一个单元,第四列地状态可以直接推得,这样枚举状态的时间就得到了优化。

const int maxn = 1005; int w[5]; char table[5][maxn]; int dp[maxn][1 << 12]; int mat[5]; // 二进制位模拟操作的矩阵 int main(){ int n = read(); for(int i = 1; i <= 4; i++) w[i] = read(); w[0] = 0; for(int i = 1; i <= 4; i++) scanf("%s", table[i] + 1); mat[0] = 0; mat[1] = 32768; // 1000 0000 0000 0000 mat[2] = 52224; // 1100 1100 0000 0000 mat[3] = 61152; // 1110 1110 1110 0000 mat[4] = 65535; // 1111 1111 1111 1111 int sta0 = 0; // 最开始的4*3的状态 for(int i = 1; i <= 4; i++) for(int j = 1; j <= 3; j++) if(table[i][j] != ‘*‘) sta0 |= 1 << (((3 - j) << 2) + (4 - i)); memset(dp, INF, sizeof(dp)); dp[0][sta0] = 0; for(int j = 1; j <= n; j++){ int last = 0; // 一个状态单元中第四列的状态 for(int i = 1; i <= 4; i++) if(table[i][j + 3] != ‘*‘) last |= 1 << (4 - i); for(int sta = 0; sta < (1 << 12); sta++){ if(dp[j - 1][sta] == INF) continue; for(int a = 0; a <= 4; a++){ for(int b = 0; b <= 3; b++){ for(int c = 0; c <= 2; c++){ for(int d = 0; d <= 1; d++){ int add = mat[a] | mat[b] >> 1 | mat[c] >> 2 | mat[d] >> 3; if((sta >> 8 | add >> 12) == 15){ // 一个状态第一列消去全部‘*‘ int cost = w[a] + w[b] + w[c] + w[d]; int nxt_sta = (sta << 4 | add | last) & 4095; dp[j][nxt_sta] = min(dp[j][nxt_sta], dp[j - 1][sta] + cost); } } } } } } } printf("%d\n", dp[n][4095]); return 0; }
[codeforces 903G] Yet Another Maxflow Problem 最大流+最小割+区间加&RMQ线段树:
直接从最大流入手是很困难的,将最大流问题转换成求最小割就好很多。拿样例说明(我们在B1上加了一条容量为0的入边,A4上加了一条容量为0的出边):
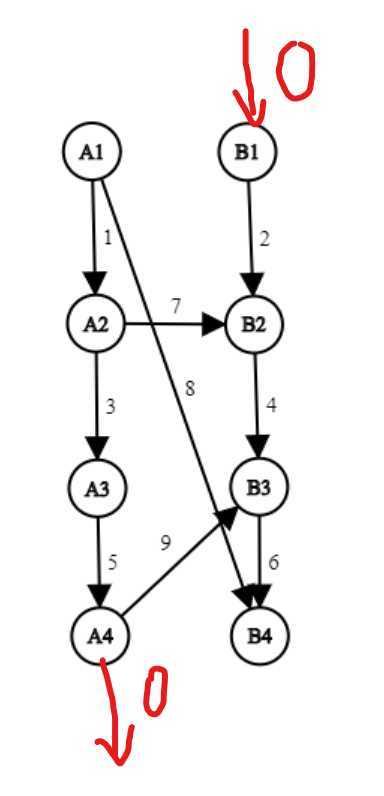
这个最小割集必定是这样的构成:A部分中有一个割边,B部分中有一个割边,A和B之间有若干割边,然后对A部分一条边做假设,假设这条边为割边,那么这条边之前的流量可以通过AB之间的边流向B,然后这条边的流量可以往后流有可能通过某条边流到B部分。然后B部分也会有相应的割边,在这条割边后可能有从A流到B部分的流量,那么最终的流量计算就是A部分一条割的流量+A部分割边之前的节点(包括割边的始点)到B的割边之后的流量+B的割边的流量。拿上图举例假设A1到A2的边为割边,然后从A1到B4的边就是AB之间的割,然后B部分的割边是那个指向B1的流量为0的边,计算得到流量为9。假设A2到A3的边为割边,然后从A1到B4和A2到B2的边就是AB的割边,然后B上的割就是B2到B3。……我是怎么知道B上的割的呢?其实就是流量,哪条边限制限制了流量那条边就是割,又变成了最大流问题,但是这是只有一条路线的最大流,用一些数据结构就可以方便修改和查找。又拿上图举例,首先我们入过没有从A流到B的流量,那么B上每个节点的流量限制就是:0,2,4,6,显然 0 是根本的限制。然后加入从A1流到B4的边,流量限制会变成:8,10,12,14,在B1到B4上都加上8,这次的流量就限制在8。
分析得差不多了,具体做法如下:
我们可以1∼n枚举每个ai,用线段树维护对应每个bj所需要的最小割的大小。首先将所有bj加入到线段树中,对于当前枚举到的ai,枚举从Ai出发的所有AB类边,若对应的点为Bj,权值为w,将区间[1,j]加上w,表示对于ai及ai以后的A类边,若还要考虑bj及bj以前的B类边作为对应边,一定要割去这条AB类边。而每次插入后线段树最小元素就是对应当前ai,由一个B类边和若干AB类边组成的、能与ai构成割的边权和,记这一边权和为sum,则选择ai时的最小割为sum+ai,记作ci。c[]中最小的元素就是对应初始网络的最大流了。
考虑修改操作,由于ai对应的B类边和C类边已经确定,每次修改时ai的变化也就是sum+ai中的ai的变化,直接改变了ci。
本题用到的是支持区间加&RMQ的线段树。

const int MAX_N = 1 << 19; // 比实际需要的叶子节点数的两倍要大 LL minx[MAX_N], addv[MAX_N]; // 对区间[a, b)同时加上x // k是结点编号,对应区间是[l, r) // 调用时传参为(左, 右, x, 0, 0, n),记得区间左闭右开 void add(int a, int b, LL x, int k, int l, int r) { int mid = (l + r) >> 1; if (a <= l && r <= b) addv[k] += x; else{ if (mid > a) add(a, b, x, k * 2 + 1, l, mid); if (mid < b) add(a, b, x, k * 2 + 2, mid, r); } minx[k] = 0; if(r - 1 > l) minx[k] = min(minx[k * 2 + 1], minx[k * 2 + 2]); minx[k] += addv[k]; } // 查询区间[a, b)最小值 // 调用的时候参数传入为(左, 右, 0, 0, n, 0),区间左闭右开 LL query_min(int a, int b, int k, int l, int r, LL add){ //[a, b)是要求的区间,[l, r)是现在递归到的区间 if(b <= l || a >= r) return LL_INF; if(a <= l && r <= b) return minx[k] + add; else{ int vl = query_min(a, b, k * 2 + 1, l, (l + r) / 2, add + addv[k]); int vr = query_min(a, b, k * 2 + 2, (l + r) / 2, r, add + addv[k]); return min(vl, vr); } } const int maxn = 2e5 + 5; LL A[maxn], B[maxn], C[maxn]; vector<pii> G[maxn]; int main(){ int n = read(), m = read(), q = read(); for(int i = 1; i < n; i++){ A[i - 1] = read(), B[i] = read(); } for(int i = 0; i < n; i++) add(i, i + 1, B[i], 0, 0, n); for(int i = 0; i < m; i++){ int x = read() - 1, y = read() - 1, w = read(); G[x].push_back(pii(y, w)); } for(int i = 0; i < n; i++){ for(int j = 0; j < G[i].size(); j++){ add(0, G[i][j].first + 1, G[i][j].second, 0, 0, n); } C[i] = A[i] + query_min(0, n, 0, 0, n, 0); } memset(addv, 0, sizeof(addv)); memset(minx, 0, sizeof(minx)); for(int i = 0; i < n; i++){ add(i, i + 1, C[i], 0, 0, n); } printf("%d\n", query_min(0, n, 0, 0, n, 0)); while(q--){ int a = read() - 1, w = read(); add(a, a + 1, w - A[a], 0, 0, n); A[a] = w; printf("%d\n", query_min(0, n, 0, 0, n, 0)); } return 0; }
Educational Codeforces Round 34 (Rated for Div. 2) 现场3题补后AK
原文:https://www.cnblogs.com/ACHappy-yjy/p/12960526.html